2. 北京儿童医院 眼科, 北京 100045
2. Ophthalmology Department, Beijing Children Hospital, Beijing 100045, China
青光眼是世界第二大致盲性疾病,在2040年之前青光眼患者的数量会达到1.1亿[1]。患者在青光眼的初期通常没有明显的症状,直到出现视觉损失时才会发现自己患病[2]。如果病人在青光眼初期就被发现,采取及时的治疗将能够有效地阻止视力衰退。因此对青光眼的早期诊断十分重要。
视网膜神经纤维层(RNFL)缺损是诊断青光眼的重要特征。在临床诊断中,光学相干断层扫描(OCT)能够直接测量RNFL厚度,被视为标准的检查结果。但是OCT检查价格昂贵,且我国多数中小型医院和体检中心并不具备相应设备。与OCT相比,眼底照检查成本低,在许多医院和体检中心被广泛使用。在眼底照上,RNFL于背景中呈现有条纹的模式,形成了特定的纹理。这些纹理会根据RNFL厚度的变化而改变[3]。因此,利用眼底照和OCT的多模态数据,设计基于眼底照来预测RNFL厚度的智能算法,不仅具有重要的临床应用价值,也具有很高的可行性。
从20世纪80年代开始,许多基于眼底照提取RNFL特征的计算机辅助算法被研究者们相继提出[3-9]。其中,Oliva等[8]提出了一种基于像素强度预测RNFL厚度的方法,并在9张正常眼和9张青光眼眼底照上进行实验,Pearson相关系数达到了0.424。Odstrcilik等[9]在使用马尔可夫随机场、局部二进制等经典的图像处理方法提取眼底照中的特征后,再通过支持向量回归模型(SVR)预测RNFL厚度,并在28张正常眼和8张青光眼眼底照上进行评估;该方法在正常眼和青光眼上的Pearson相关系数分别为0.72和0.58,均方根误差分别为26.06和25.09。然而以上文献使用的传统方法无法自动提取眼底照的RNFL信息,回归预测值与真实值的偏差较大,而且没有在大样本数据集上进行验证。近年来,深度学习在计算机视觉领域快速发展,并在医学图像领域取得了巨大进步[10-11]。姚红革等[12]将深度学习方法应用在目标定位的回归任务上,在公开数据集COCO 2014上达到先进水平。然而据我们所知,目前还没有研究工作利用深度学习方法基于眼底照对视盘外围局部区域的RNFL厚度进行预测。
本文设计了一种深度残差回归神经网络,实现了自动提取眼底照中的特征并预测视网膜神经乳头附近的RNFL厚度。利用本文设计的深度学习回归算法,可以用较低的成本预测出眼底照中的RNFL厚度,量化评估眼底照中的青光眼性损伤,进而用于辅助青光眼的诊断。
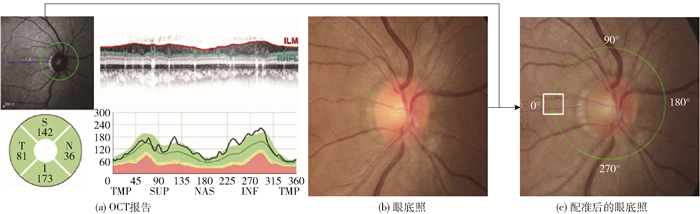
1 视网膜神经纤维层数据集的构建 1.1 数据采集本文采集关于青光眼诊断的两种不同的检查数据,即眼底照片和OCT检查报告。这两种检查数据均为图像数据,其中眼底照片为眼底照相机拍摄的RGB彩色照片,如图 1(b)所示。而OCT是一种基于低相干光干涉原理, 利用样品反射光与参考光相干进行成像的非接触性新型成像技术[13]。OCT检查报告如图 1(a)所示,本文仅使用此报告中左上角和右下角两块区域内的图像信息,其中,左上角图像为低分辨率的眼底照,图像中的绿色圆圈表示OCT测量RNFL厚度的位置及方向;右下角图像中的黑色曲线表示上述绿色圆圈上的RNFL厚度值。利用Matlab提取这一黑色曲线在360°范围内的数值,存储为RNFL厚度向量,如第i张眼底照的RNFL厚度向量的第j个分量记为Tji, 其中i=1, 2, …, 136;j=1, 2, …, 360。
|
图 1 OCT报告与眼底照配准示意图 Fig.1 Registration of OCT report and fundus image |
本文所用数据来源于北京同仁医院,均取自15 d内同时做过眼底照相、OCT检查的正常人和青光眼患者的检查结果,共计136只眼,来自于136个人,其中有107个正常眼和29个青光眼。
1.2 图像配准为了获取OCT报告中RNFL厚度曲线在眼底照中所对应的位置,首先对彩色眼底照和OCT报告中的低分辨率眼底照进行图像配准。本文使用PhotoShop软件进行人工手动配准。在PhotoShop中将彩色眼底照置于底层,把这张眼底照对应的OCT报告中的低分辨率眼底照调整为半透明后置于顶层,通过调整低分辨率眼底照的位置和角度使两者的血管重合,便完成配准。配准后即可得到OCT扫描路径在彩色眼底照中的位置,记录下扫描路径所在圆周的圆心位置αi和半径ri。
1.3 图像切分根据1.2节记录下的αi和ri,在第i张眼底照上从0°开始沿顺时针方向旋转τ°,第k次旋转后在圆周上对应的点记为Ck*τi。以Ck*τi为中心在彩色眼底照上切分出边长为S的正方形区域Rki,作为一个patch。将Rki中心像素点的厚度值Tk*τi作为Rki的标注,其中k=1, 2, …, 360/τ。后续实验中设置S=65, τ=4。
1.4 数据划分本文采用5折交叉验证的方式进行实验。在每折交叉验证中,对于每张眼底照,在连续排列的5个patch中选择1个划入测试集,它的前一个划入验证集,剩下的3个划入训练集。划分之后,训练集共7 344个patch,验证集共2 448个patch,测试集共2 448个patch,它们的组成如表 1所示。在第g折交叉实验中,第g组作为测试集,其余4组数据分别作为训练集和验证集(g=1, 2, 3, 4, 5)。训练集用于训练本文所提深度学习网络以获得预测模型,验证集用于选择网络的超参数,测试集不参与模型的训练。最终,根据算法对5折交叉验证实验中测试集的预测来计算平均绝对误差EMA(MAE)、决定系数和Pearson相关系数。
| 下载CSV 表 1 训练集、验证集和测试集的组成 Table 1 Components of train, validation and test dataset |
基于眼底照中的正方形区域RGB图像来预测该区域的局部RNFL厚度是一个回归问题,因此我们设计了一种包含残差模块[14]的深度神经网络来完成这一回归预测过程。
残差模块最早出现于残差分类网络ResNet中,ResNet是ILSVRC2016比赛分类项目的冠军,其跳跃连接结构提高了卷积层提取特征的能力并解决了深层神经网络中的梯度消失问题[15]。但是相比于VGG16和Inception V3等网络,经典的ResNet模型由于参数过多而使得模型复杂度较高。为了精简模型参数,本文利用全局平均池化层(GAP)来处理卷积层提取的特征。同时,将ResNet的损失函数由交叉熵损失替换为均方误差损失,用于回归预测任务。
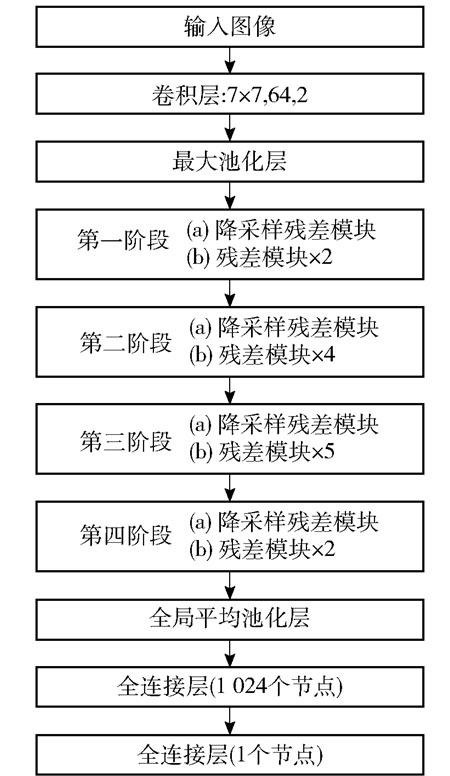
2.1 网络主体结构以残差神经网络为主体结构,搭建了如图 2所示的深度残差回归神经网络。网络的输入是大小为65×65的RGB图像,输入图像经过卷积核大小为7、卷积核个数为64、步长为2的卷积层后,通过最大池化层减小维度,依次经过降采样残差模块与残差模块。经过最后一个残差模块后连接全局平均池化层,后面加入全连接层,通过批标准化(BN)处理后以线性整流函数ReLU激活,再加入随机失活率为0.7的DropOut层,最后使用只有1个输出节点的全连接层作为回归网络的输出。
|
图 2 深度残差回归神经网络结构图 Fig.2 Architecture of the deep residual regression network |
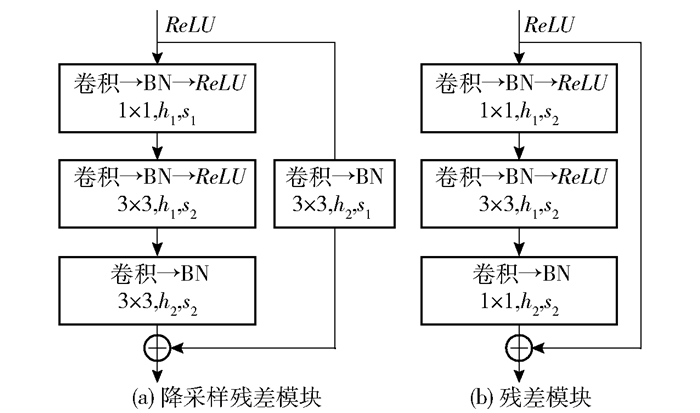
降采样残差模块的详细结构如图 3(a)所示,模块的输入经过一个ReLU激活层后有两个分支,第一个分支依次经过3层卷积操作后,与第二个分支经过1个卷积操作的结果进行逐元素相加,作为降采样残差模块的输出。残差模块如图 3(b)所示,模块的输入经过一个ReLU激活层后有两个分支,第一个分支依次经过3层卷积操作,之后与第二个分支进行逐元素相加作为残差模块的输出。图 3中h1和h2表示卷积核个数,s1和s2表示卷积操作的步长。每个阶段中降采样残差模块和残差模块的参数设置如表 2所示。
|
图 3 降采样残差模块和残差模块 Fig.3 Sampling residual module and residual module |
| 下载CSV 表 2 深度残差神经网络中每个阶段的参数设置 Table 2 Parameters in each stage of the deep residual network |
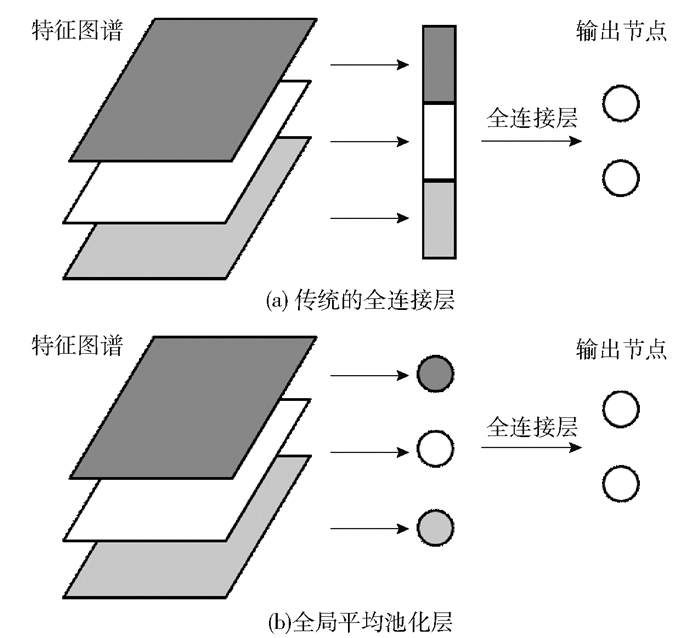
传统的全连接层如图 4(a)所示,上一个卷积层输出的特征图谱伸展为一维向量后,经过全连接层与输出节点相连。全连接层的参数量与这个向量的长度成正比,当特征图谱维度过大时,全连接层的参数量激增,不仅增加了模型的体积也延长了计算时间。
|
图 4 全连接层与全局平均池化层 Fig.4 Fully connected layer and global average pooling layer |
全局平均池化层如图 4(b)所示,对于上一个卷积层输出的特征图谱,将每个通道的特征图的元素值累加求平均,每个通道的特征图生成一个特征点,全部通道的特征点组合成的一维特征向量经过全连接层与输出节点相连。将上一卷积层的特征图谱用Fp, q, k表示,其中(p, q, k)分别表示特征图谱的长、宽和通道数,当输出节点数为l时,传统的全连接层需要的参数量为p ·q ·k·l,而使用全局平均池化层时的参数量为k ·l,减小为全连接层的$\frac{1}{{pq}}$,大大降低了模型参数规模。
2.4 损失函数与优化器损失函数选择均方误差损失EMS(MSE)来表示,计算公式为
| $ E_{\mathrm{MS}}\left(y, y^{\prime}\right)=\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{i}-y_{i}^{\prime}\right)^{2} $ | (1) |
式中,yi和y′i分别表示第i个样本的真实值与算法预测值,mm。
选择随机梯度下降法作为优化器,每次从全部样本中随机选择一个样本计算损失函数的梯度,沿着负梯度方向前进减小损失函数的值,通过不断地更新权重使得损失函数值达到最小,此时的权重即为最优。
2.5 评估指标选择平均绝对误差、决定系数R2和Pearson相关系数r作为算法的评估指标。这3种评估指标的表达式如下。
| $ \begin{aligned} E_{\mathrm{MA}}=& \frac{1}{n} \sum\limits_{i=1}^{n}\left\|y_{i}-y_{i}^{\prime}\right\| \end{aligned} $ | (2) |
| $ \begin{aligned} R^{2}=& \frac{\sum\limits_{i=1}^{n}\left(y_{i}^{\prime}-\bar{y}\right)^{2}}{\sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}} \end{aligned} $ | (3) |
| $ r=\frac{\sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)\left(y_{i}^{\prime}-\bar{y}^{\prime}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2} \sum\limits_{i=1}^{n}\left(y_{i}^{\prime}-\bar{y}^{\prime}\right)^{2}}} $ | (4) |
式中,y和y′分别表示样本真实值的平均值和预测值的平均值,$\bar{y}=\frac{1}{n} \sum\limits_{i=1}^{n} y_{i}, \bar{y}^{\prime}=\frac{1}{n} \sum\limits_{i=1}^{n} y_{i}^{\prime}$,单位均为mm。
3 实验结果分析 3.1 实验设置本文提出的深度学习回归模型在以Tensorflow为底端的Keras框架下实现,使用的设备是一台装有两块NVIDIA1080tiGPU的工作站。Tensorflow版本1.4.1,Keras版本2.0.1, Ubuntu系统版本16.04,内存64 G。
将原始图像的像素值除以255缩放至[0, 1]区间。本文采用迁移学习的方法,卷积层的初始参数通过对ResNet50在ImageNet数据集[16]上训练获得,并对全连接层的参数作随机赋值;进而利用训练集,通过最小化损失函数进一步调整网络各层的参数。使用5折交叉验证的方式对本文算法进行验证,训练过程中batchsize设置为64,迭代次数epoch设置为120,随机梯度下降法的学习率设置为10-4。在训练过程中选择使验证集损失最小的模型作为最终的模型,并验证这一模型在测试集上的预测性能。
3.2 结果分析对本文所提算法在测试集上进行验证,作为比较,也验证了VGG16、InceptionV3、Xception和经典ResNet50(不含全局平均池化层)等网络框架用于回归预测时的预测性能,结果如表 3所示。
| 下载CSV 表 3 不同深度学习网络在测试集上的评估指标 Table 3 Performance of different deep learning networks on the test set |
从表 3可以看出,与VGG16、InceptionV3和Xception相比,经典ResNet50具有更小的MAE、更大的R2和r,但是模型体积增加较大。与经典ResNet50相比,本文提出的加入GAP的残差网络模型体积减小了19.6%,预测精度与其大致相当:MAE略有减小,R2略有降低,r略微提升。从综合性能考虑,本文所提方法的预测效果最佳。
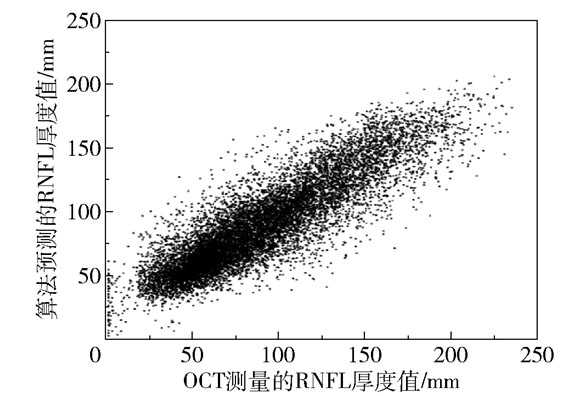
图 5展示了本文方法对RNFL厚度的预测值与OCT测量值的分布,可以看到两者之间存在强相关性(r=0.878,P < 0.001)。算法预测的RNFL厚度均值为(88.45±1.39) mm,OCT测量的RNFL厚度均值为(89.69±1.67) mm。进一步,分别在正常眼和青光眼上计算了算法预测值与OCT测量值的相关性,得到对于正常眼r=0.885,对于青光眼r=0.872。
|
图 5 算法预测值与OCT测量值的分布 Fig.5 Distribution of prediction and OCT |
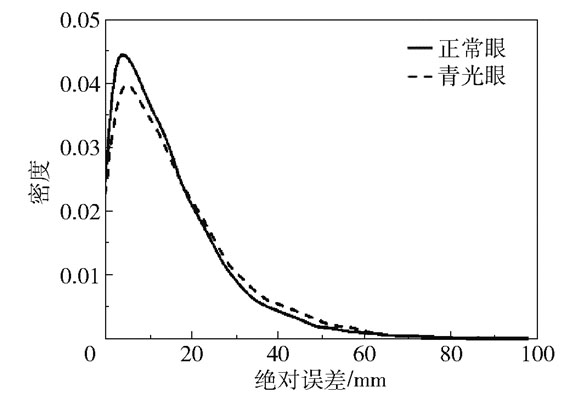
为了分别观察正常眼和青光眼的绝对误差分布,图 6展示了在两组不同数据上绝对误差的密度分布曲线。可以看出,正常眼与青光眼的绝对误差的密度分布曲线比较相似,误差值大部分都分布在20 mm以下,其中正常眼在[0, 20]区间的比例更高。正常眼的预测绝对误差为(14.884±12.522) mm,青光眼的预测绝对误差为(15.108±13.215) mm,青光眼的值略高,但差异不明显。
|
图 6 绝对误差在正常眼和青光眼上的分布 Fig.6 Distribution of absolute error in normal and glaucomatous eyes |
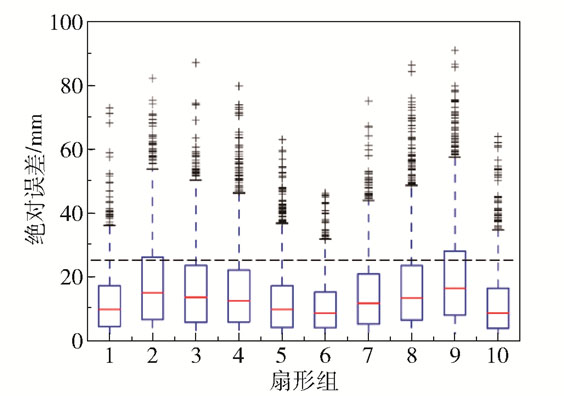
为了观察绝对误差在360°范围内不同角度处的分布,将眼底照以配准后所得圆心为中心,从0°开始等分出10个扇形组,将每个扇形组的绝对误差以箱线图的形式展示在图 7中。在箱线图中,矩形的水平上边框和水平下边框分别表示绝对误差的3/4分位数和1/4分位数,矩形内部的水平直线表示中位数,矩形上方的“+”表示奇异值。可以看出,多数扇形区域的绝对误差的3/4分位数都分布在25 mm以下,每个扇形区域内都有少数奇异点大于30 mm。其中第2组和第9组的箱线图整体分布的位置更高,且3/4分位数超过25 mm,远高于其他组。这两组分别对应36°~72°和288°~324°(视网膜神经乳头左上侧和左下侧),这两处的血管较粗且分布较为密集,影响了模型在附近区域提取RNFL特征的性能。然而,即使是不同的OCT设备,测量出的RNFL厚度值也会存在10~25 mm的差异[9],因此本文方法的误差是可以接受的。
|
图 7 算法预测值的绝对误差在不同角度的分布 Fig.7 Distribution of the predicted absolute errors at different angles |
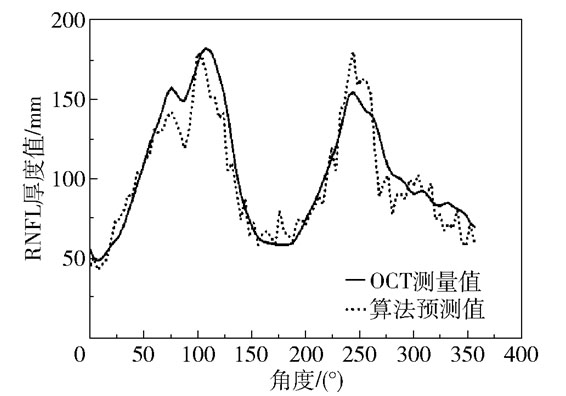
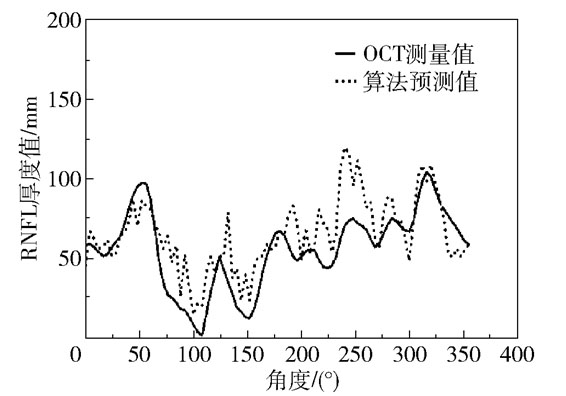
进一步在整张眼底照上进行了算法预测值与OCT测量值的对比。图 8展示了在一张正常眼眼底照上本文算法预测的RNFL厚度值和OCT测量值的对比,可以看到正常眼的预测曲线与OCT测量曲线在各个位置都很接近,两者均刻画出了正常眼的典型双峰结构。图 9展示了在一张青光眼眼底照上本文算法预测的RNFL厚度值与OCT测量值的对比,同样可以看到预测曲线与OCT测量曲线在绝大多数位置都很接近,而且在70°~170°之间准确预测出了此处的RNFL厚度接近于0,表明此处存在RNFL缺损。
|
图 8 正常眼上算法预测值与OCT测量值的对比 Fig.8 Comparison between the prediction and OCT on a normal eye |
|
图 9 青光眼上算法预测值与OCT测量值的对比 Fig.9 Comparison between the prediction and OCT on a glaucomatous eye |
本文基于眼底照和OCT的多模态数据,提出了基于眼底照中的局部区域信息预测RNFL厚度的智能算法。我们设计了以残差卷积结构提取图像特征、以全局平均池化层与全连接层输出回归预测值的深度残差回归神经网络。在真实数据集上的实验结果验证了本文算法具有较低的平均绝对误差和较高的统计相关性。通过本文算法,可以基于成本较低的眼底照来预测RNFL厚度,也可以与其他青光眼类指标联合来辅助青光眼的诊断。
| [1] |
THAM Y C, LI X, WONG T Y, et al. Global prevalence of glaucoma and projections of glaucoma burden through 2040: a systematic review and meta-analysis[J]. Ophthalmology, 2014, 121(11): 2081-2090. DOI:10.1016/j.ophtha.2014.05.013 |
| [2] |
XU Y L, LU S, LI H X, et al. Mixed maximum loss design for optic disc and optic cup segmentation with deep learning from imbalanced samples[J]. Sensors, 2019, 19(20): 4401. DOI:10.3390/s19204401 |
| [3] |
PELI E, HEDGES III T R, SCHWARTZ B. Computer measurement of retinal nerve fiber layer striations[J]. Applied Optics, 1989, 28(6): 1128-1134. DOI:10.1364/AO.28.001128 |
| [4] |
TUULONEN A, ALANKO H, HYYTINEN P, et al. Digital imaging and microtexture analysis of the nerve fiber layer[J]. Journal of Glaucoma, 2000, 9(1): 5-9. DOI:10.1097/00061198-200002000-00003 |
| [5] |
LEE S Y, KIM K K, SEO J M, et al. Automated quantification of retinal nerve fiber layer atrophy in fundus photograph[C]//Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Francisco, 2004: 1241-1243.
|
| [6] |
HAYASHI Y, NAKAGAWA T, HATANAKA Y, et al. Detection of retinal nerve fiber layer defects in retinal fundus images using Gabor filtering[C]//Proceedings of SPIE 6514, Medical Imaging 2007: Computer-Aided Diagnosis. San Diego, 2007: 65142Z.
|
| [7] |
HWANG J M, KIM T W, PARK K H, et al. Correlation between topographic profiles of localized retinal nerve fiber layer defects as determined by optical coherence tomography and red-free fundus photography[J]. Journal of Glaucoma, 2006, 15(3): 223-228. DOI:10.1097/01.ijg.0000212218.96932.f7 |
| [8] |
OLIVA A M, RICHARDS D, SAXON W. Search for color-dependent nerve-fiber-layer thinning in glaucoma: a pilot study using digital imaging techniques[J]. Investigative Ophthalmology & Visual Science, 2007, 48(13): 3309. |
| [9] |
ODSTRCILIK J, KOLAR R, TORNOW R P, et al. Thickness related textural properties of retinal nerve fiber layer in color fundus images[J]. Computerized Medical Imaging and Graphics, 2014, 38(6): 508-516. DOI:10.1016/j.compmedimag.2014.05.005 |
| [10] |
侯向丹, 赵一浩, 刘洪普, 等. 融合残差注意力机制的UNet视盘分割[J]. 中国图象图形学报, 2020, 25(9): 1915-1929. HOU X D, ZHAO Y H, LIU H P, et al. Optic disk segmentation by combining UNet and residual attention mechanism[J]. Journal of Image and Graphics, 2020, 25(9): 1915-1929. (in Chinese) |
| [11] |
张悦, 余双, 马锴, 等. 人工智能关于视盘区多任务深度学习模型在青光眼分类中的应用[J]. 中华眼科医学杂志(电子版), 2020, 10(2): 70-75. ZHANG Y, YU S, MA K, et al. The application of artificial intelligence multi-task deep learning model of optic disc area in the classification of glaucoma[J]. Chinese Journal of Ophthalmologic Medicine (Electronic Edition), 2020, 10(2): 70-75. (in Chinese) |
| [12] |
姚红革, 张玮, 杨浩琪, 等. 深度强化学习联合回归目标定位[J/OL]. 自动化学报, 2020[2020-09-25]. https://doi.org/10.16383/j.aas.c200045. YAO H G, ZHANG W, YANG H Q, et al. Joint regression object localization based on deep reinforcement learning[J/OL]. Acta Automatica Sinica, 2020[2020-09-25]. https://doi.org/10.16383/j.aas.c200045. (in Chinese) |
| [13] |
陆冬筱, 房文汇, 李玉瑶, 等. 光学相干层析成像技术原理及研究进展[J]. 中国光学, 2020, 13(5): 919-935. LU D X, FANG W H, LI Y Y, et al. Optical coherence tomography: principles and recentdevelopments[J]. Chinese Optics, 2020, 13(5): 919-935. (in Chinese) |
| [14] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, 2016: 770-778.
|
| [15] |
郭玥秀, 杨伟, 刘琦, 等. 残差网络研究综述[J]. 计算机应用研究, 2020, 37(5): 1292-1297. GUO Y X, YANG W, LIU Q, et al. Survey of residual network[J]. Application Research of Computers, 2020, 37(5): 1292-1297. (in Chinese) |
| [16] |
DENG J, DONG W, SOCHER R, et al. ImageNet: a large-scale hierarchical image database[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Miami, 2009: 248-255.
|








