2. 中国电子科技集团公司 第四十一研究所, 青岛 266555
2. The 41st Research Institute, China Electronics Technology Instruments Co., Ltd., Qingdao 266555, China
爆炸爆温是指炸药爆炸时放出的能量将爆炸产物加热到的最高温度,它是评估炸药性能的一个重要指标。爆炸过程具有破坏力强、电磁干扰力强、温度高、温度动态范围大等特点,爆炸场温度数据的采集与测量难度高,目前尚没有非常有效的测试技术及设备,因此,基于爆炸温度场的非接触测量重建方法研究具有重要的实际应用价值。近年来,爆炸温度场的测量与重建得到了许多研究人员的关注[1-5]。郭晓杰等[1]结合高速摄像技术和辐射测温法实现了瞬态高温场的测试。范航[4]研究了爆炸温度场的代数重建(algebraic reconstruction techniques,ART)算法、联合代数重建(simultaneous algebraic reconstruction technique, SART)算法与乘法代数重建(multiplicative algebraic reconstruction technology,MART)算法仿真,并给出了一种改进的多准则迭代重构(multi criteria iterative reconstruction,MCIR)算法进行温度场分布的仿真重建。徐维铮等[5]根据自主开发的数值计算程序开展密闭空间内炸药爆炸温度场的数值计算,初步探讨了内爆炸温度场演化过程及其分布规律。
随着计算机技术和数字图像技术的进步,基于图像的温度场三维重建方法研究得到了迅速发展。温度场三维重建方法主要结合在医学诊断、无损检测等领域常用的计算机断层成像技术来实现基于火焰图像的温度场三维重建。Gordon等[6]提出了经典的代数重建技术,然而经典ART方法由于其边缘效应,重建质量不高。Gilbert[7]提出了一种优化的ART方法以降低对噪声的敏感度,也即同时迭代重建(simultaneous iterative reconstruction technology,SIRT)算法,该方法中的像素值在每次迭代中均使用平均像素值进行更新,从而达到更好的降噪效果,但收敛速度降低。Andersen等[8]提出了ART的另一种变形方法,该方法通过二次优化SIRT方法有效地提高了ART算法的收敛速度,即联合代数重建算法。SART是一种在图像三维重建中应用较为广泛的迭代重建算法,许多研究人员将其应用于医学计算机断层扫描(CT)图像的重建[9-14]、微波图像重建[15-17]以及电力系统的电容层析成像[11]等方面。冀东江等[9]对SART算法进行改进,提出了在分母加上惩罚项的惩罚SART算法,其惩罚项的思想是减小畸变处的迭代步长以减弱畸变。乔全邦等[10]提出了一种基于模糊熵的自适应联合代数算法应用于CT图像重建;该方法采用模糊熵对图像进行边缘提取,并根据边缘一致性原则构造单调递增函数,将该单调递增函数定义为迭代步长的松弛算子,从而进行图像重建,它解决了重建图像边缘模糊的问题,还可以抑制振铃效应。针对电容层析成像中图像重建算法的非线性和病态问题,宋亚杰等[18]将SART算法应用于电容层析成像,提高了图像重建速度,并且重建图像的边缘信息保真度较高。Han等[15]提出了一种在SART算法中插入非线性因子的改进方法,该方法在特定的84个投影点的情况下可以取得较好的收敛效果,但在不满足特定条件的情况下算法不收敛。Donato等[11]通过使用双边正则化滤波器对CT图像进行滤波以改进图像的重建质量,并在显卡(GPU)上对乳腺样本进行了图像重建。Tiwari等[12]使用各向异性扩散作为正则化方法改进了SART的迭代方法,提高了CT图像的重建质量。Aprilliyani等[16]和Ramdani等[17]将SART算法应用于微波系统中肿瘤的检测或癌症的无创层析成像系统的开发上,利用3 GHz的微波信号,通过特定位置的发射端和接收端来采集数据,成功重构了图像。Zhang等[13]改进了SART算法中投影矩阵的计算方法,使其计算速度得到显著提高。Sabah等[14]讨论了简单反投影、滤波反投影和迭代算法的性能参数,并认为与迭代重建中的其他方法相比,SART算法改善了图像质量,减少了重建误差并产生了条纹痕迹。
尽管SART的改进算法对于抑制图像畸变、提高重建质量起到了一定的作用,但传统的畸变校正方法只对边缘区域的抑制作用明显,在校正畸变时并不遵循某一最优准则,并且由于爆炸场高温数据获取困难的特点,在投影角度较少的情况下,重建图像依然会出现明显的边缘效应,并且边缘效应会使重建图像和原始图像的辐射积分误差趋近于零,导致迭代无法进行,使得重建图像中间区域失真严重,无法达到重建要求。因此,针对爆炸场温度瞬时性的特点,本文借鉴惩罚思想并融合均匀性准则对SART算法的迭代步长进行改进,所采用的变迭代步长方法能有效地抑制畸变和边缘效应,提高图像重建质量。
1 改进的SART算法 1.1 惩罚SART算法SART算法是温度场重建中一种常见的迭代重建算法[6],该算法的基本思想是在同一截面内对通过某一像素的不同方向的射线校正值进行累加来校正该像素值,其迭代公式为
| $ f_{j}^{(k+1)}=f_{j}^{(k)}+\lambda \frac{\sum\limits_{p_{i} \in \boldsymbol{P}}\left(\lambda \frac{p_{i}-\sum\limits_{n=1}^{N} w_{i n} f_{n}^{(k)}}{\sum\limits_{n=1}^{N} w_{i n}}\right) w_{i j}}{\sum\limits_{p_{i} \in \boldsymbol{P}} w_{i j}} $ | (1) |
式中,fj(k)表示第j个网格点中的像素值,wij表示第j个像素点对第i条射线的影响,pi表示第i条射线的投影值,P表示投影值集合,λ为迭代系数,决定迭代步长,取值范围为(0, 1]。
SART算法可以使理论计算值逼近实际测量值,但是当投影数据含有噪声时,重建图像中的噪声随迭代次数不断累加,导致图像重建效果不佳。为了解决这一问题,冀东江等[9]通过在权值中增加惩罚项来改进SART算法,其迭代公式为
| $ f_{j}^{(k+1)}=f_{j}^{(k)}+\lambda \frac{\sum\limits_{p_{i} \in \boldsymbol{P}}\left(\lambda \frac{p_{i}-\sum\limits_{n=1}^{N} w_{i n} f_{n}^{(k)}}{\sum\limits_{n=1}^{N} w_{i n}}\right) w_{i j}}{\sum\limits_{p_{i} \in \boldsymbol{P}} w_{i j}+y_{j}^{(k)}} $ | (2) |
其中
| $ \begin{aligned} &y_{j}^{(k)}= \\ &\left\{\begin{array}{l} \alpha \sum\limits_{i \in N_{j}}\left(f_{j}^{(k)}-f_{i}^{(k)}\right), &\sum\limits_{i \in N_{j}}\left(f_{j}^{(k)}-f_{i}^{(k)}\right) \geqslant 0 \\ \alpha \sum\limits_{i \in N_{j}}\left(f_{j}^{(k)}-f_{i}^{(k)}\right)+\beta, &\sum\limits_{i \in N_{j}}\left(f_{j}^{(k)}-f_{i}^{(k)}\right)<0 \end{array}\right. \end{aligned} $ | (3) |
式中,Nj表示所有与j相邻的像素点,fi(k)为与fj(k)相邻区域的像素点,α、β为惩罚系数。yj(k)项的加入相当于对投影修正值施加了惩罚作用,一般情况下,相邻像素间的像素值是接近的,参数变化较为平缓,所以其局部应是均匀的。未发生畸变时,
惩罚SART算法的思想是通过牺牲迭代速度,减小校正值以减弱畸变,提高重建质量,但该方法对所有区域均使用统一的迭代步长,导致在边缘区域畸变依然明显。因此,本文采用变迭代步长的惩罚方式,以有效抑制边缘区域的畸变,在SART算法满足的最小二乘准则中加入均匀性准则,提高重建质量。
考虑到实际测量时相邻像素间的灰度值是接近的,即参数变化较为平缓,所以针对像素间的关系提出均匀性准则,即
| $ \phi=o^{2} f_{j}^{(k)}-\sum\limits_{i \in N_{j}} f_{i}^{(k)} $ | (4) |
式中,o为区域长度,可由使用者自行选择;Nj为与fj(k)相邻的判定区域;fj(k)为判断是否产生畸变的像素点;ϕ为判断该像素点是否产生畸变的判定系数,当ϕ值超过某一人为界定的数值时,即判定该像素点产生畸变。将该判定以惩罚的方式代入SART算法的迭代系数λ中,即可在SART算法满足的最小二乘准则中加入均匀性准则,从而提高图像的重建质量。
迭代系数λ体现了校正值的权重,其值一般取0~1。λ值较大时,由于迭代较快,畸变也会被放大;λ值太小,则会使迭代速度过慢。采用变迭代步长是希望在无畸变处λ能取较大值,不影响迭代速度,而在有畸变处λ能取较小值,以减小迭代步长,抑制畸变。为实现这种效果,本文改进了迭代系数表达式,如式(5)所示。
| $ \lambda=\frac{f_{j}^{(k)}}{f_{j}^{(k)}+y_{j}^{(k)}} $ | (5) |
其中
| $ \begin{array}{ll} \ \ \ \ \ \ y_{j}^{(k)}= \\ \left\{\begin{array}{ll} \alpha\left(o^{2} f_{j}^{(k)}-\sum\limits_{i \in N_{j}} f_{i}^{(k)}\right), & o^{2} f_{j}^{(k)}-\sum\limits_{i \in N_{j}} f_{i}^{(k)} \geqslant 0 \\ \alpha\left(o^{2} f_{j}^{(k)}-\sum\limits_{i \in N_{j}} f_{i}^{(k)}\right)+\beta, & o^{2} f_{j}^{(k)}-\sum\limits_{i \in N_{j}} f_{i}^{(k)}<0 \end{array}\right. \end{array} $ | (6) |
式中, fj(k)为判断是否需要惩罚的像素点。以3×3的惩罚区域为例,其示意图如图 1所示。α为无畸变时的惩罚系数,应尽可能小以不影响迭代步长,β为产生畸变时的惩罚系数,应尽可能大以抑制畸变。式(5)和式(6)可保证λ取值范围仍为0~1。
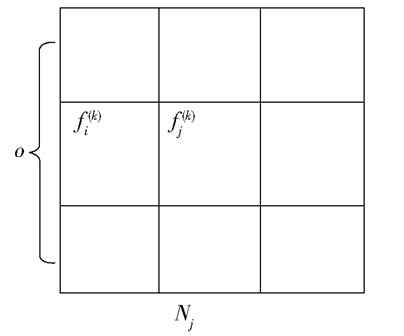
|
图 1 3×3的惩罚区域示意图 Fig.1 3×3 penalty area diagram |
将式(5)代入式(1)可得到变迭代步长SART算法公式为
| $ f_{j}^{(k+1)}=f_{j}^{(k)}+\frac{f_{j}^{(k)}}{f_{j}^{(k)}+y_{j}^{(k)}} \frac{\sum\limits_{p_{i} \in \boldsymbol{P}}\left(\frac{p_{i}-\sum\limits_{n=1}^{N} w_{i n} f_{n}^{(k)}}{\sum\limits_{n=1}^{N} w_{i n}}\right) w_{i j}}{\sum\limits_{p_{i} \in \boldsymbol{P}} w_{i j}} $ | (7) |
作为SART算法的改进,变迭代步长SART算法与SART算法都满足最小二乘准则,即使得δ=(P-WF)T(P-WF)有最小值,其中W为投影矩阵,F为温度场的迭代值。这是因为对迭代系数λ的改进不改变SART算法逐点迭代的特点。但该算法具备了更好的抑制畸变的能力,还能有效消除值为0处的畸变,即当fj(k)值为0时,其值将一直保持为0不再迭代,因而使用该算法时应使迭代初值不为0。
综上所述,基于变迭代步长SART算法的步骤可归纳如下。
1) 将原图像分别旋转0°、45°、90°并向x轴投影,用得到的辐射积分图像模拟测量值。
2) 根据旋转角度构建相应的投影矩阵W。
3) 给定计算初值Fo。
4) 确定惩罚区域长度o与惩罚系数α、β。
5) 根据惩罚区域与惩罚系数计算惩罚项yj(k)。
6) 将投影矩阵W、初值Fo、惩罚项yj(k)代入式(7)。
7) 判断式(7)计算结果是否满足终止条件,如满足,退出迭代;否则执行步骤5)进行下一次迭代。
2 实验结果与分析 2.1 实验验证为检验本文改进的算法,采用如式(8)所示的函数模拟三维温度场的分布情况以进行测试[4]。
| $ \begin{array}{l} \ \ \ \ \ \ \ f(x, y)=\exp \left\{-\frac{\left[(x-25)^{2}+(y-25)^{2}\right]}{80}\right\}- \\ \exp \left\{-\frac{\left[(x+25)^{2}+(y-25)^{2}\right]}{80}\right\}+\exp \cdot\\ \left\{-\frac{\left[x^{2}+(y+25)^{2}\right]}{80}\right\} \end{array} $ | (8) |
所得函数图像如图 2所示,可以看出图形有两个正高斯峰和1个负高斯峰,可用来模拟复杂情况下的三维温度场分布。
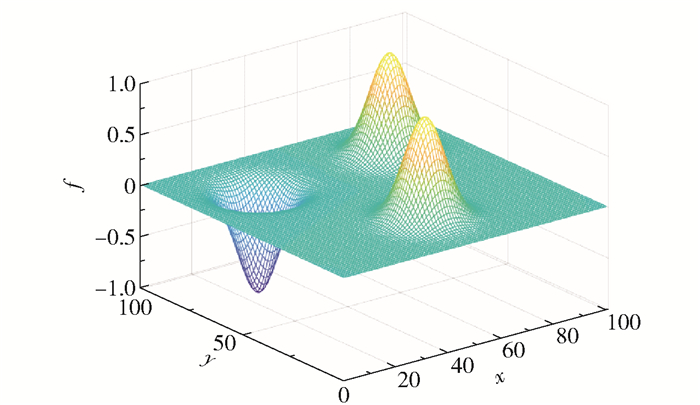
|
图 2 模拟多峰函数图像 Fig.2 Analog image multimodal function |
在仿真实验中,采用0°、45°、90°这3个角度的辐射积分图像进行重建,得到的辐射积分图像如图 3所示。
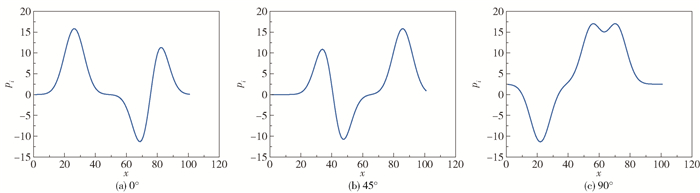
|
图 3 辐射积分图像 Fig.3 Radiation integral images |
本文采用辐射积分误差e和峰值误差m作为评价标准,其计算公式为
| $ e=\|\boldsymbol{P}-\boldsymbol{W} \boldsymbol{F}\| $ | (9) |
| $ m=1-\max (\boldsymbol{F}) $ | (10) |
在第一组仿真实验中,将惩罚项系数设定为α=0.000 01,β=15,惩罚区域分别设定为5×5、11×11和31×31。迭代算法终止条件为辐射积分误差e < 5。
从图 4的仿真结果可以看出,变迭代步长的SART算法重建图像的正峰和负峰都在函数所描述位置附近,方向均正确,值为0的区域畸变明显消除。
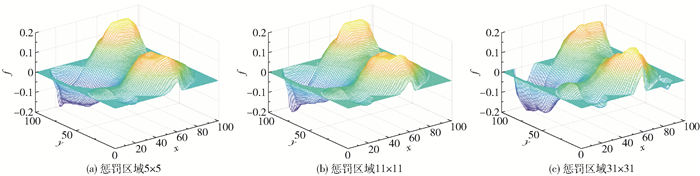
|
图 4 第一组仿真实验的三维重建图像 Fig.4 Three-dimensional reconstruction images for the first set of simulation experiments |
由图 5的辐射积分误差曲线图可以看出惩罚区域为11×11的结果相比于惩罚区域5×5的结果收敛更快,只经过21次迭代即可将误差降低至5以下,且波峰和波谷的范围更小,形状更加突出;而当惩罚区域扩大至31×31后,迭代加快,但边缘效应也更加明显,逐渐失去抑制畸变的能力。
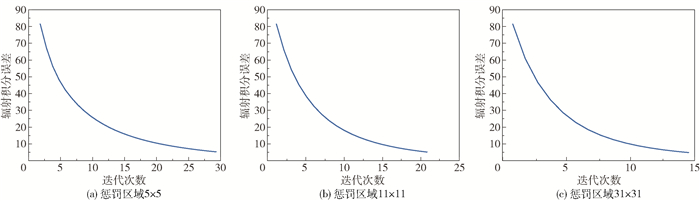
|
图 5 第一组仿真实验的重建辐射积分误差曲线 Fig.5 Plots for reconstruction of radiation integral error for the first set of simulation experiments |
由图 6的峰值误差曲线可以看出,惩罚区域为11×11的峰值误差在0附近,这说明重建函数最大值接近原函数。惩罚区域为5×5的峰值误差出现负值,说明重建函数最大值超过了原函数最大值,这是因为惩罚区域过小,图像对正常区域进行了过度的惩罚,抑制了正常的迭代过程,为减小辐射积分误差而在峰值区域出现迭代值过大的情况。惩罚区域为31×31的峰值误差在0.1附近,这是因为惩罚区域选择过大导致峰值误差较大,从而无明显的惩罚作用。
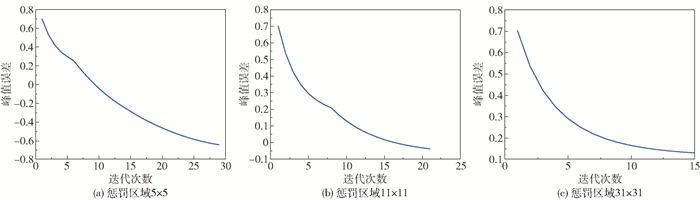
|
图 6 第一组仿真实验的峰值误差曲线 Fig.6 Plots for peak error for the first set of simulation experiments |
由上可知,惩罚区域选择过大,会失去惩罚作用,导致图像重建效果不佳;惩罚区域选择过小,会因为过度惩罚增加迭代次数而使峰值过大;而选择合适的惩罚区域,则可以改善重建图像的质量。因此,针对不同图像选择合适的惩罚系数和惩罚区域可达到兼顾重建质量和收敛速度的效果。
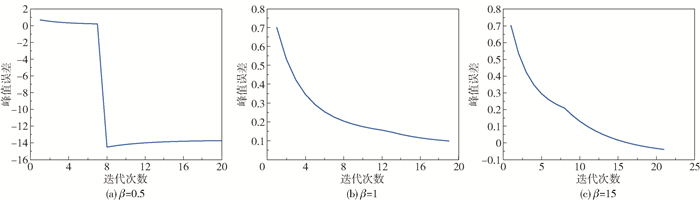
2.1.2 第二组仿真实验在第二组仿真实验中,将惩罚区域设定为11×11,改变惩罚项系数进行实验,即当α=0.000 01时,β依次取值0.5、1、15,所得仿真结果如图 7~9所示。
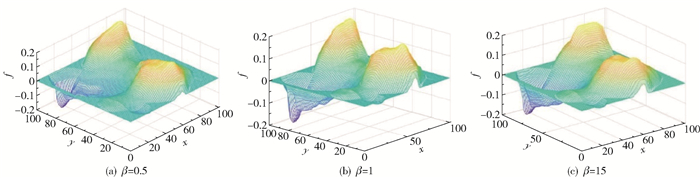
|
图 7 第二组仿真实验的三维重建图像 Fig.7 Three-dimensional reconstruction images for the second set of simulation experiments |
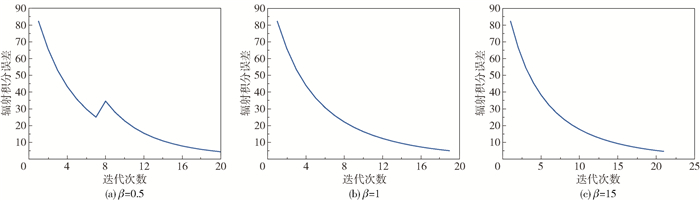
|
图 8 第二组仿真实验的重建辐射积分误差曲线 Fig.8 Plots for reconstruction of radiation integral error for the second set of simulation experiments |
|
图 9 第二组仿真实验的峰值误差曲线 Fig.9 Plots for peak error for the second set of simulation experiments |
由图 8和图 9可以看出,在3种β取值所得辐射积分误差相近的情况下,β=15时峰值误差有较好的表现;当β=1时,因惩罚系数较小,对畸变的抑制作用较弱,而使峰值不突出,峰值误差较大;β=0.5时,惩罚系数过小甚至使惩罚项yj(k)值为负,完全丧失惩罚作用,峰值误差和辐射积分误差出现较大突变。
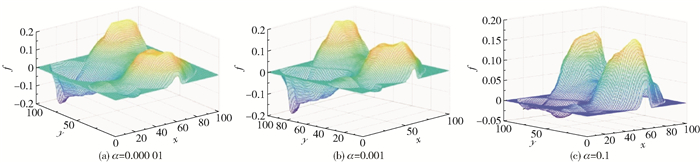
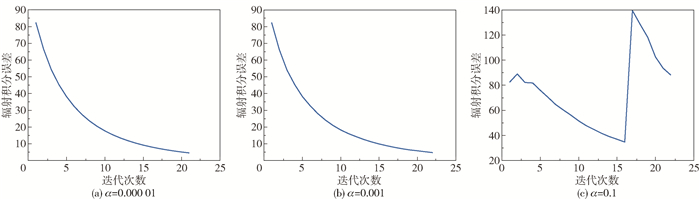
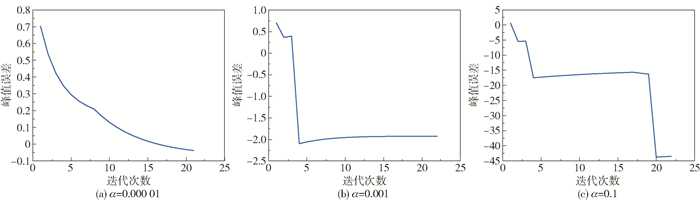
2.1.3 第三组仿真实验在第三组仿真实验中,将惩罚区域设定为11×11,β取值为15时,α依次取值0.000 01、0.001、0.1,所得仿真结果如图 10~12所示。
|
图 10 第三组仿真实验的三维重建图像 Fig.10 Three-dimensional reconstruction images for the third set of simulation experiments |
|
图 11 第三组仿真实验的重建辐射积分误差曲线 Fig.11 Plots for reconstruction of radiation integral error for the third set of simulation experiments |
|
图 12 第三组仿真实验的峰值误差曲线 Fig.12 Plots for peak error for the third set of simulation experiments |
由图 11和图 12可以看出,当α=0.000 01和α=0.001时辐射积分误差可以迭代至较低水平,α=0.1时辐射积分误差过大且有较大波动;α= 0.000 01时图像峰值误差有较好的表现,α=0.001时图像峰值误差产生突变,α=0.1时图像甚至无法收敛。这是因为α作为无畸变时的惩罚系数,取值应尽可能的小,当惩罚区域判定为无畸变时,通过乘以α使判定值减小而使惩罚项yj(k)较小以不影响迭代过程;当惩罚区域判定为有畸变时,通过乘以α使判定值减小,再与β相加而使惩罚项yj(k)较大以抑制畸变。α取值过大会在无畸变时使惩罚项yj(k)过大而抑制正常的迭代过程,在有畸变时则可能使惩罚项yj(k)过小甚至为负从而失去惩罚作用。
2.2 不同重建算法的比较本文还对比了变迭代步长SART算法、SART算法和惩罚SART算法迭代30次的重建图像,其中变迭代步长SART算法和惩罚SART算法的惩罚区域均为11×11,惩罚项系数均为α=0.000 01,β=15,所得结果见图 13~15。
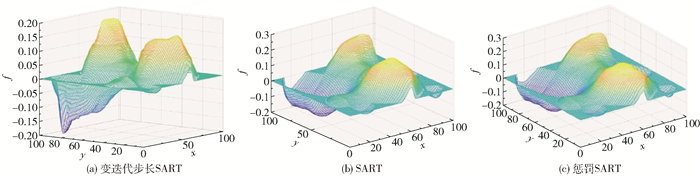
|
图 13 3种不同算法的三维重建图像 Fig.13 Three-dimensional reconstruction images for three different algorithms |

|
图 14 3种不同算法的重建辐射积分误差曲线 Fig.14 Plots for reconstruction of radiation integral error for three different algorithms |
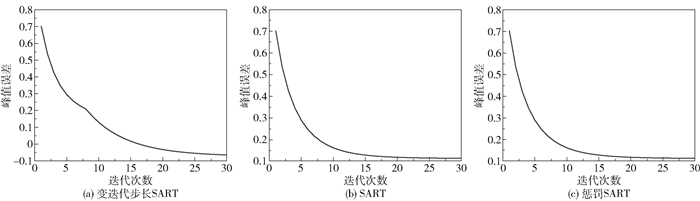
|
图 15 3种不同算法的峰值误差曲线 Fig.15 Plots for peak error for three different algorithms |
由图 13可以看出,SART算法和惩罚SART算法对图像的还原度较高,收敛快,但存在畸变,特别是在值为0的边缘区域畸变较为明显。变迭代步长的SART算法不仅能还原图像,还能明显消除值为0的区域的畸变,使峰值区域更突出。
由图 14、15可知,在3种算法的辐射积分误差相近的情况下,SART及惩罚SART算法的峰值误差均在0.1以上,其值较大。变迭代步长的SART算法具有较高的收敛速度,在30次迭代后辐射积分误差较小,峰值误差在0.1以下,接近原函数峰值。
3 结论针对传统SART算法、惩罚SART算法在图像重建过程中存在的误差较大,尤其是边缘畸变突出的问题,本文提出了一种改进的SART算法。本文所提改进算法在原有的最小二乘准则上融合了均匀性准则,即对畸变的判定与校正采用均匀性准则,对不满足这一准则的区域进行惩罚以抑制畸变,对满足这一准则的区域不作处理。该准则不仅适用于边缘区域,且对图像所有区域均适用。传统的畸变校正方法只对边缘区域的畸变抑制作用明显,且在校正畸变时并不遵循某一准则,没有特定的判定标准。相比之下,本文方法中对畸变惩罚系数可以人为设定,根据重建图像的不同设定合适的判定系数,可以兼顾重建速度和质量。实验结果表明本文方法优势在于能有效抑制图像的边缘效应产生的畸变,提高重建质量;并且其惩罚项的系数和惩罚区域可针对不同的图像自由选择,选择合适的惩罚系数和惩罚区域可以获得更好的重建质量和较高的收敛速度。但该改进方法是以牺牲迭代步长为代价的,因此优化耗时较长,对于大图像精细重建需要的时间较久,难以及时得到重建结果。
| [1] |
郭晓杰, 郝晓剑, 周汉昌. 基于CCD辐射能图像的爆炸温度场技术研究[J]. 中国测试, 2017, 43(12): 16-20. GUO X J, HAO X J, ZHOU H C. Technical research on explosion temperature field based on CCD radiation energy image[J]. China Measurement and Test, 2017, 43(12): 16-20. (in Chinese) DOI:10.11857/j.issn.1674-5124.2017.12.004 |
| [2] |
吕秀莲. 基于CCD图像传感器的高温温度场测量研究[D]. 南京: 南京理工大学, 2012. LV X L. Research on the measurement of high temperature field based on CCD image sensor[D]. Nanjing: Nanjing University of Science and Technology, 2012. (in Chinese) |
| [3] |
李艳秋, 刘石. 基于三维变分的声学法三维温度场重建[J]. 热力发电, 2017, 46(10): 52-57. LI Y Q, LIU S. Reconstruction of three-dimensional temperature field using 3DVAR-based acoustic method[J]. Thermal Power Generation, 2017, 46(10): 52-57. (in Chinese) |
| [4] |
范航. 爆炸温度场三维测量技术研究[D]. 西安: 西安工业大学, 2017. FAN H. Study on 3D measurement technology of explosion temperature field[D]. Xi'an: Xi'an Technological University, 2017. (in Chinese) |
| [5] |
徐维铮, 吴卫国. 密闭空间内爆炸温度场数值计算及其特性研究[J]. 应用力学学报, 2020, 37(1): 280-285, 487-488. XU W Z, WU W G. Numerical calculation of explosion temperature field and its characteristics in closed space[J]. Chinese Journal of Applied Mechanics, 2020, 37(1): 280-285, 487-488. (in Chinese) |
| [6] |
GORDON R, BENDER R, HERMAN G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J]. Journal of Theoretical Biology, 1970, 29(3): 471-481. DOI:10.1016/0022-5193(70)90109-8 |
| [7] |
GILBERT P. Iterative methods for the three-dimensional reconstruction of an object from projections[J]. Journal of Theoretical Biology, 1972, 36(1): 105-117. DOI:10.1016/0022-5193(72)90180-4 |
| [8] |
ANDERSEN A H, KAK A C. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm[J]. Ultrasonic Imaging, 1984, 6(1): 81-94. DOI:10.1177/016173468400600107 |
| [9] |
冀东江, 曾理, 邹晓兵. 锥束CT的惩罚SART重建算法[J]. 计算机工程与应用, 2008, 44(28): 152-154, 165. JI D J, ZENG L, ZOU X B. Penalty of SART reconstruction algorithm for cone-beam CT[J]. Computer Engineering and Applications, 2008, 44(28): 152-154, 165. (in Chinese) DOI:10.3778/j.issn.1002-8331.2008.28.051 |
| [10] |
乔全邦, 黄力宇, 贺志杰. 一种自适应的CT图像联合代数重建算法[J]. 西安电子科技大学学报, 2016, 43(3): 67-72. QIAO Q B, HUANG L Y, HE Z J. Image reconstruction using an adaptive simultaneous algebraic reconstruction technique in computed tomography[J]. Journal of Xidian University, 2016, 43(3): 67-72. (in Chinese) DOI:10.3969/j.issn.1001-2400.2016.03.012 |
| [11] |
DONATO S, BROMBAL L, ARFELLI F, et al. Optimization of a customized simultaneous algebraic reconstruction technique algorithm for breast CT[C]//2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). Manchester: IEEE, 2019: 1-2.
|
| [12] |
TIWARI S, CHOUKSEY D, TODWAL V. Regularization based simultaneous algebraic reconstruction techniques for computed tomography[C]//2016 Ninth International Conference on Contemporary Computing (IC3). Noida: IEEE, 2016: 1-6.
|
| [13] |
ZHANG S L, GENG G H, CAO G H, et al. Fast projection algorithm for LIM-based simultaneous algebraic reconstruction technique and its parallel implementation on GPU[J]. IEEE Access, 2018, 6: 23007-23018. DOI:10.1109/ACCESS.2018.2829861 |
| [14] |
SABAH S, DHOU S. Three-dimensional CT image reconstruction techniques: implementation and comparison[C]//2019 International Conference on Communications, Signal Processing, and their Applications (ICCSPA). Sharjah, 2019: 1-6.
|
| [15] |
HAN Y, SONG Y Z. Precise reconstruction achieved with the simultaneous algebraic reconstructing technique inserted our nonlinear iterative factor[C]// Proceedings of 2019 IERI International Conference on Economics, Management, Applied Sciences and Social Science. Berlin, 2019: 548-552.
|
| [16] |
BASARI, APRILLIYANI R. The effect of data acquisition configuration on simultaneous algebraic reconstruction technique algorithm for microwave imaging system[C]//2018 Asia-Pacific Microwave Conference (APMC). Kyoto: IEEE, 2018: 1405-1407.
|
| [17] |
RAMDANI S, ASTYANI A P, BASARI. Filtered back projection and simultaneous algebraic reconstruction technique for image formation on square-shaped physical phantom aimed at microwave imaging applications[C]//2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama). Toyama: IEEE, 2018: 464-469.
|
| [18] |
宋亚杰, 张立峰, 朱炎峰. 基于联合代数重建的电容层析成像图像重建[J]. 电力科学与工程, 2018, 34(7): 44-48. SONG Y J, ZHANG L F, ZHU Y F. Image reconstruction for electrical capacitance tomography based on simultaneous algebraic reconstruction technique[J]. Electric Power Science and Engineering, 2018, 34(7): 44-48. (in Chinese) |








