2. 北京化工大学 教育部高分子材料加工装备工程研究中心, 北京 100029
2. Polymer Processing Equipment Engineering Research Center, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
在过去的几十年中,复合材料由于具有出色的特性,例如比刚度高、比强度高、制品结构可设计性强、热稳定性好、质轻、疲劳极限高和使用寿命长等,因而其得到了广泛应用[1]。纤维增强树脂基复合材料中的树脂基体一般分为热固性树脂和热塑性树脂两种。热固性复合材料的单向预浸料已经发展了很多年并且广泛应用于航空航天、汽车等领域[2-4],但是热固性材料仍然存在成型周期长、局部损伤难以修复、无法重复使用等缺点[5-7]。与热固性复合材料相比,热塑性复合材料具有高韧性、高抗冲击、成型周期短、生产效率高、易修复、可回收、成本低等优点,这一系列对比使得纤维增强热塑性复合材料在汽车轻量化、节能、可持续发展的背景下拥有广阔的发展前景。但由于热塑性树脂在浸渍纤维的过程中需要高压和高温条件,通常热塑性基体的浸渍条件比热固性基体要差,这将大大削弱热塑性复合材料的机械性能,因此如何优化浸渍条件一直是制备热塑性复合材料需要解决的主要问题之一[8]。
热塑性复合材料根据纤维残留长度的不同主要分为短切纤维复合材料(SFRT)、长纤维增强复合材料(LFRT)和连续纤维增强复合材料(CFRTP)。连续纤维增强复合材料的制备方法主要包括原位聚合技术、粉末浸渍法、混编法和熔融浸渍法。其中,熔融浸渍法的工艺简单,在生产过程中基本不产生污染物,并且成本低廉、可连续化生产,其制备的预浸料的质量更易控制。熔融浸渍模具是熔融浸渍工艺的核心区域,其结构优化是提高预浸带性能的关键之一[9-11]。赫晓霞[9]利用数值模拟仿真技术模拟模具内的熔体压力分布,分析了模具结构及工艺参数对浸渍效果的影响,并优化设计了一种辊系熔融浸渍模具,实验结果表明所制备的复合材料的浸渍效果良好。孙立坤[10]设计了一套辊系结构和一套齿系结构的熔融浸渍模具,通过实验分析两种结构模具的优缺点,发现齿系结构模具的浸渍和分散效果更好。孙海青[11]设计了一种周向建压浸渍的齿系熔融浸渍模具,研究了模具结构对连续纤维浸渍效果的影响,优化了模具结构并制备得到了浸渍质量良好的复合材料。上述研究对制备复合材料的浸渍模具优化方向进行了探索,但是制备单向预浸带的齿系浸渍模具仍然存在一些不足,如单向预浸带的拉伸性能较低,纤维分散均匀度较低等。因此需要对齿系浸渍模具结构进行系统的研究和优化设计。
连续纤维增强预浸带浸渍模具的浸渍效果主要通过纤维浸渍程度和纤维断裂率这两个指标来表征,浸渍模具的各项结构参数对这两个指标的影响不一且存在参数交互影响,浸渍模具的设计难点主要在于如何解决这两个指标的矛盾。纤维浸渍程度和纤维断裂率都与制备预浸带的牵引速度密切相关,合理的浸渍模具结构不仅可以提高预浸带性能,也可以提高优质预浸带的产能。
常用的熔融浸渍模具主要有辊系式和弯曲流道式两种类型,其中,弯曲流道式模具因其良好的浸渍和分散效果而广泛应用于工业领域中。为了研究可以制备出优质预浸带的弯曲流道式浸渍模具结构,探究模具结构参数对预浸带各项性能的影响,本文采用自行设计的两种模具制备预浸带,测试表征其性能。以袁满等[12]的理论模型为基础,建立纤维浸渍模型和断裂模型。结合实验结果验证模型,并分析模具结构对预浸带性能的影响。
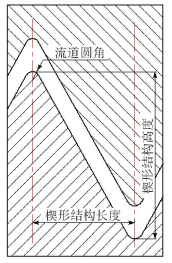
1 纤维浸渍模型和断裂模型 1.1 模具结构分析弯曲流道式模具一般由数个相同的楔形结构组成,其结构如图 1所示。楔形结构的主要参数为楔形结构长度、楔形结构高度和流道圆角半径等。
|
图 1 楔形结构示意图 Fig.1 Schematic diagram of the wedge structure |
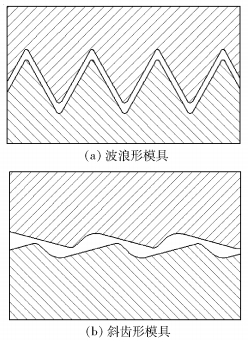
图 2为波浪形和斜齿形模具的结构示意图。波浪形模具的上下模板流道壁面相对平行,且收敛的楔形区长度较长。而相同模具流道长度的斜齿形模具的主楔形区个数是波浪形模具的两倍,楔形区长度较短,流道单元高度和流道圆角半径均较小。
|
图 2 波浪形和斜齿形模具结构示意图 Fig.2 Schematic diagrams of the wavy and helical mold structures |
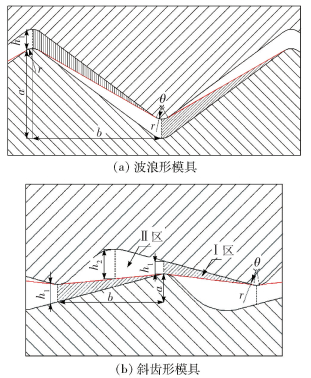
两种模具的楔形结构参数示意图如图 3所示。其中,a为楔形区单元流道顶端到底端的垂直距离(流道单元高度),b为楔形区单元流道顶端到底端的水平距离(流道单元长度),θ为单个流道圆角处的纤维包覆角,r为流道圆角半径,h1为模具间隙(主楔形区入口高度),h2为副楔形区入口高度。斜齿形模具在浸渍过程中每个楔形结构处同时存在两个收敛的楔形区,可以对纤维上下表面同时浸渍, 如图 3(b)中Ⅰ和Ⅱ区域所示,Ⅰ区域为主楔形区,Ⅱ区域为副楔形区。设计这两种模具旨在探索在相同浸渍流道长度的模具中楔形结构对模具浸渍效果的影响。
|
图 3 波浪形和斜齿形模具的楔形结构参数示意图 Fig.3 Schematic diagrams of wedge structural parameters of the wavy and helical molds |
弯曲流道式模具中每个楔形区的浸渍效果都随着楔形区结构的变化而变化,模具的浸渍效果为模具中所有楔形区的浸渍效果总和。理论模型中两种楔形结构的浸渍效果的计算方法完全一致,只需要根据楔形结构参数改变对应楔形区的结构参数即可。两种模具的重要结构参数对比如表 1所示。
| 下载CSV 表 1 两种模具的结构参数 Table 1 Structural parameters of the two molds |
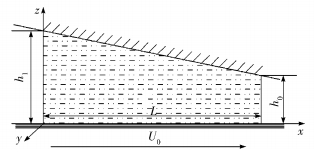
单个楔形区内建立相应的直角坐标系,楔形区的简化结构如图 4所示。其中,L为楔形区长度,h0为楔形区出口高度,U0为纤维牵引速度。左侧为楔形区入口,右侧为楔形区出口,斜面为模具流道壁面,中间为熔融树脂,下侧若干直线表示纤维束。
|
图 4 楔形区示意图 Fig.4 Schematic diagram of the wedge zone structure |
纤维在模具内实际的熔融浸渍过程是一个比较复杂的工艺过程,因此做出以下假设以简化纤维浸渍模型:1)熔体不受重力、体积力、惯性力等附加力场的作用,且不考虑毛细管效应;2)浸渍模具中熔体的流动都是由纤维束拖曳产生的层流流动且无滑移现象,纤维束内部的熔体只沿纤维径向流动;3)浸渍过程中纤维束横截面为矩形,纤维单丝呈均匀排列并保持不变。
纤维截面示意图如图 5所示。熔体在纤维中的浸渍过程可以看作流体在多孔介质中流动,一般采用达西定律来描述[13],树脂沿纤维径向的浸渍速度u的计算公式参见文献[14]。

|
图 5 纤维截面示意图 Fig.5 Schematic diagram of the fiber section Kozen y- Carman(KC) |
方程可以用来描述在均匀排列的纤维束形成的多孔介质中流体的浸渍过程[15]。Yazdchi等[16]推导了树脂在纤维束中的渗透率预测公式,如式(1)所示,并发现当纤维束的孔隙率为0.5~0.7时渗透率较稳定。
| $ {K_i} = \frac{{{d^2}\phi _i^3}}{{{k_0}{{\left( {1 - {\phi _i}} \right)}^2}}} $ | (1) |
式中,Ki为第i个楔形区的树脂渗透率,d为纤维单丝直径,ϕi为将要进入第i个楔形区前的纤维束的孔隙率,k0为Kozen y- Carman常数(一般取120)。
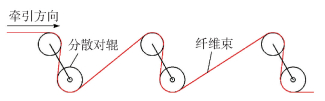
浸渍过程中纤维展宽主要受纤维预分散设备的影响,本文所用的预分散设备为自行设计的机械辊,结构如图 6所示。每一束玻璃纤维中有几千根玻璃纤维,其中的受力情况无法具体分析,纤维预分散展宽与预分散辊半径、纤维所受包覆角、牵引速度等有关,因此可以通过实验建立对经过预分散装置后纤维束的展宽进行预测的经验公式。
|
图 6 分散辊示意图 Fig.6 Schematic diagram of the dispersing roller |
通过设计两因素三水平一响应的实验,由Design Expert软件对实验数据分析,得到纤维分散展宽的预测经验公式为
| $ B = 8.624 - 0.1625{U_0} + 0.012235J $ | (2) |
式中,B为纤维束展宽,J为预分散纤维包覆角。
楔形区出口高度h0一般为纤维束与流道圆角的熔体膜厚度,可以通过式(3)计算[17]。
| $ {h_0} = 1.4rf{\left( {\frac{{{U_0}\eta B}}{T}} \right)^{\frac{2}{3}}} $ | (3) |
式中,f为浸渍系数(熔融浸渍所用纤维束的f值为0.5),η为熔体黏度,T为纤维束预紧张力。
一般楔形区入口高度h1近似于流道间隙Δh。斜齿形模具楔形区Ⅱ区的出口高度即为楔形区Ⅰ区的入口高度,楔形区Ⅱ区的入口高度h2则根据实际结构参数,通过式(4)求解。
| $ {h_2} = a + \left( {\frac{{2{a^2}}}{{{a^2} + {b^2}}}} \right)\Delta h $ | (4) |
弯曲流道式模具内的熔体压力根据袁满等[12]对雷诺方程的积分求解,得到楔形区的平均压力P为
| $ \overline p = \frac{{5\eta {U_0}L\left[ {{\rm{ln}}\frac{{{h_1}}}{{{h_0}}} - \frac{{2\left( {{h_1} - {h_0}} \right)}}{{{h_1} + {h_0}}}} \right]}}{{{{\left( {{h_1} - {h_0}} \right)}^2}\left[ {1 + g{{\left( {\frac{L}{B}} \right)}^2}} \right]}} $ | (5) |
式中,g为模具结构系数。波浪形模具和斜齿形模具每个楔形区Ⅰ区的平均压力可通过式(5)求解。在计算斜齿形模具楔形区Ⅱ区熔体的平均压力时,将h0、h1分别替换为h1、h2。
在弯曲流道式浸渍模具中每个楔形区只对纤维束的单面浸渍,所以模具中纤维束的上下表面为交替浸渍,浸渍过程中上下表面的浸渍深度需要单独计算。联立式(1)~(5)可得纤维束经过N次单侧浸渍的浸渍深度ZN为
| $ {Z_N} = \sum\limits_{i = 1}^N {\sqrt {\frac{{2{K_i}{{\overline P }_i}{L_i}}}{{\eta {U_0}}}} } $ | (6) |
式中,P i为第i个楔形区的熔体平均压力,Li为第i个楔形区的长度。
根据纤维束横截面为矩形的假设,可以通过计算得到纤维束厚度H,计算公式同袁满等[12]对纤维束厚度的计算方法,则浸渍时的KC方程中纤维渗透孔隙率ϕi按纤维束单侧浸渍的计算公式为
| $ {\phi _i} = {\phi _0}\left( {1 - \frac{{{Z_{\left( {i - 1} \right)}}}}{H}} \right) $ | (7) |
式中,ϕ0为纤维初始孔隙率(一般取0.5),Z(i-1)为第i个楔形区前的单侧纤维束浸渍深度。
弯曲流道式浸渍模具的楔形区一般以成对设计出现,则纤维束的上下两侧浸渍的楔形区个数相同且浸渍程度相同,所以最终纤维束的整体浸渍深度为2Z(i-1),则浸渍完成的理论纤维束孔隙率ϕ为
| $ {\phi _i} = {\phi _0}\left( {1 - \frac{{{Z_{\left( {i - 1} \right)}}}}{{\frac{H}{2}}}} \right) $ | (8) |
在模型的计算过程中,当ϕ≤0时,纤维束浸渍完成,渗透率K=0。纤维的理论浸渍程度D为
| $ D = 1 - {\phi _0}\left( {1 - \frac{{{Z_{\left( {i - 1} \right)}}}}{{\frac{H}{2}}}} \right) $ | (9) |
采用三参数的Carreau模型对树脂熔体黏度η进行表征[18],黏度变化规律如式(10)所示。
| $ \eta = {\eta _0}{\left[ {1 + {{\left( {\lambda \dot \gamma } \right)}^2}} \right]^{\frac{{n - 1}}{2}}} $ | (10) |
式中,η0为零剪切黏度,Pa ·s;λ为松弛时间,s;
为了降低黏度计算过程的复杂性,整个楔形区内的熔体可以取楔形区中点处的剪切速率进行计算,则一般楔形区的熔体剪切速率为
| $ \dot \gamma = \frac{{2{U_0}}}{{{h_1} + {h_0}}} $ | (11) |
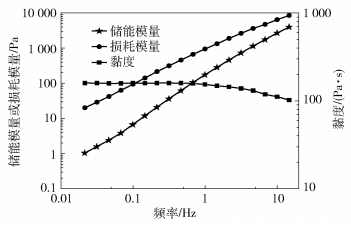
采用旋转流变仪(HAAKE MARS型,德国赛默飞世尔科技有限公司)测量BX3920聚丙烯树脂在230 ℃下的流变性能,得到树脂熔体的黏度变化曲线,如图 7所示。采用Carreau模型对流变曲线进行拟合,得到树脂的流变参数,如表 2所示。
|
图 7 树脂黏度特性曲线 Fig.7 Viscosity characteristic curves of the resin |
| 下载CSV 表 2 树脂熔体的流变参数 Table 2 Rheological parameters of the resin melts |
纤维浸渍模型中针对熔融浸渍过程提出的基本假设也适用于纤维断裂模型,同时为了简化计算做出以下假设:1)纤维单丝所受的黏性拖曳力只沿纤维轴向方向;2)纤维断裂只存在于预分散装置与浸渍模具中,且断裂的纤维不会停留在模具内。
本实验中纤维在预浸带熔融浸渍过程中的断裂过程分为两个阶段:第一阶段为纤维经过预分散装置时受机械辊作用发生断裂;第二阶段为纤维在浸渍模具内受树脂熔体和浸渍模具结构作用产生的断裂。
在预分散过程中,仅考虑纤维束在分散辊表面上的弯曲应力。在模具内浸渍过程中,只考虑纤维上下两侧受到树脂熔体的黏性拖曳力和纤维在弯曲流道壁面上的弯曲应力。
单侧每个楔形区中最外层纤维受到的黏性拖曳力F由黏性剪切应力τzx积分得到。
| $ F = \int_0^L {{\tau _{zx}}Bdx = \frac{{\eta {U_0}BL}}{{{h_1} - {h_0}}}\ln } \frac{{{h_1}}}{{{h_0}}} $ | (12) |
拖曳应力σ1为
| $ {\sigma _1} = \frac{{2NF}}{{{N_c}\frac{{\pi d_{\rm{f}}^2}}{4}}} $ | (13) |
式中,Nc为纤维束分散后的单层纤维单丝根数,N为单侧主楔形区个数,df为纤维单丝直径。
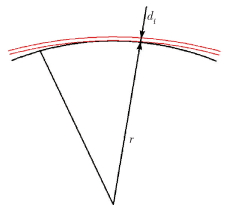
预分散辊半径为r1,浸渍模具流道圆角半径为r2,由于df≪r2 < r1,且熔体膜厚度h0≪r2 < r1,分析弯曲过程时h0可以忽略[19]。纤维的弯曲过程如图 8所示。
|
图 8 纤维弯曲示意图 Fig.8 Schematic diagram of fiber bending |
预分散装置处纤维弯曲应变ε2为
| $ {\varepsilon _2} = \frac{{\left( {{r_1} + {d_{\rm{f}}}} \right){\theta _1} - \left( {{r_1} + 0.5{d_{\rm{f}}}} \right){\theta _1}}}{{\left( {{r_1} + 0.5{d_{\rm{f}}}} \right){\theta _1}}} = \frac{{{d_{\rm{f}}}}}{{2{r_1} + {d_{\rm{f}}}}} \approx \frac{{{d_{\rm{f}}}}}{{2{r_1}}} $ | (14) |
式中,θ1为单个分散辊处的纤维包覆角。
弯曲应力σ2为
| $ {\sigma _2} = E{\varepsilon _2} $ | (15) |
式中,E为弹性模量,Pa。
则浸渍模具处纤维弯曲应变ε3为
| $ {\varepsilon _3} \approx \frac{{{d_{\rm{f}}}}}{{2{r_2}}} $ | (16) |
弯曲应力σ3为
| $ {\sigma _3} = E{\varepsilon _3} $ | (17) |
用Weibull分布函数来描述纤维的断裂过程,二参数的Weibull分布函数为[19]
| $ {P_\sigma } = 1 - {{\rm{e}}^{ - {{\left( {\frac{\sigma }{{{\sigma _0}}}} \right)}^m}}} $ | (18) |
式中,Pσ为纤维断裂概率;e为自然常数;σ为纤维所受应力,Pa;σ0为Weibull分布函数的尺度参数;m为Weibull分布函数的形状参数。
纤维束的外侧纤维受到黏性拖曳力和弯曲应力的作用,内层纤维只受弯曲应力的作用,因此纤维束经过浸渍模具浸渍后,纤维断裂概率Pσ由内侧纤维断裂概率Pσ1和外侧纤维断裂概率Pσ2组成,其计算公式如式(19)所示。
| $ \begin{array}{l} \;\;\;\;\;\;{P_\sigma } = {P_{\sigma 1}} + {P_{\sigma 2}} = \frac{{2{N_{\rm{e}}}}}{{{N_{\rm{f}}}}}[1 - {{\rm{e}}^{ - {{\left( {\frac{{{\sigma _1} + {\sigma _2} + {\sigma _3}}}{{{\sigma _0}}}} \right)}^m}}}] + \\ \frac{{\left( {{N_{\rm{f}}} - 2{N_{\rm{c}}}} \right)}}{{{N_{\rm{f}}}}}[1 - {{\rm{e}}^{ - {{\left( {\frac{{{\sigma _2} + {\sigma _3}}}{{{\sigma _0}}}} \right)}^m}}}] \end{array} $ | (19) |
式中,Nf为纤维束中的纤维单丝总根数。
将浸渍模具的结构数据及工艺参数代入理论模型中计算,即得出理论纤维浸渍程度和理论纤维断裂率。
2 实验部分 2.1 实验材料聚丙烯,BX3920,SK股份有限公司;玻璃纤维,SE4849,欧文斯科宁(中国)投资有限公司。
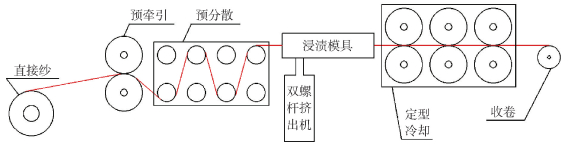
2.2 实验设备及工艺参数预浸带制备设备采用实验室自行设计的预浸带生产线,如图 9所示。
|
图 9 预浸带生产线示意图 Fig.9 Schematic diagram of the prepreg tape production line |
工艺参数和辊系浸渍模具结构参数对浸渍程度存在交互影响,李莹[20]研究发现牵引速度、温度与辊个数和辊半径的交互影响显著,辊系与齿系结构浸渍模具的浸渍原理相似,因此在研究浸渍模具结构参数对浸渍效果的影响时,两模具制备预浸带时采用相同的工艺参数,以使研究分析结果更为准确可靠。
主要工艺参数为:加工温度230 ℃,牵引速度6 m/min,预分散包覆角440°,螺杆转速180 r/min。通过调整两种熔融浸渍模具上下模板的间隙,分别制备得到5组纤维质量分数为50%的预浸带样品,并对预浸带样品进行测试表征。受实验设备和模具自身结构的限制,波浪形模具和斜齿形模具各自可连续制备预浸带的最小模具间隙不同,因此实验中两结构的起始模具间隙不一。
2.3 测试与表征 2.3.1 预浸带孔隙率采用孔隙率来表征预浸带的浸渍程度。预浸带中孔隙所占的表观体积分数即孔隙率,浸渍程度越好,预浸带的孔隙率越低。按照ASTM D273 4- 09[21],采用密度测试仪(PMM D- A型,北京冠测精电仪器设备有限公司)测试孔隙率,计算公式为[18]
| $ \varphi = \frac{{{\rho _{\rm{T}}} - {\rho _{\rm{M}}}}}{{{\rho _{\rm{T}}}}} \times 100\% $ | (20) |
其中,
| $ {\rho _{\rm{T}}} = \frac{m}{{\left( {{m_{\rm{r}}}/{\rho _{\rm{r}}}} \right) + \left( {{m_{\rm{f}}}/{\rho _{\rm{f}}}} \right)}} $ | (21) |
| $ {\rho _{\rm{M}}} = \frac{m}{V} $ | (22) |
式中,ϕ为孔隙率,ρT为预浸带理论密度,ρM为预浸带表观密度,ρr为树脂密度,ρf为纤维密度,m为预浸带质量,mr为预浸带中树脂质量,mf为预浸带中纤维质量,V为预浸带表观体积。
2.3.2 纤维断裂率纤维经过浸渍模具浸渍后纤维断裂根数占纤维束纤维总根数的比值即纤维断裂率,可通过计算纤维束浸渍前后的线密度损失来表征[22]。每组取5个样品,测量长度后放入马弗炉(SX 2- 4- 10型,武汉亚华电炉有限公司)煅烧(550 ℃,4 h),记录预浸带样品在煅烧后的纤维总质量,并把对应值代入式(23)中计算纤维断裂率[18]。
| $ {P_{\rm{f}}} = \frac{{{T_0} - {T_1}}}{{{T_0}}}100\% $ | (23) |
其中,
| $ {T_1} = \frac{{{M_{{\rm{ef}}}}}}{L} $ | (24) |
式中,Pf为纤维断裂率,T0为理论初始线密度,T1为预浸带中剩余纤维线密度,Mef为预浸带中剩余纤维质量,L为5个预浸带样品的总长度。
2.3.3 界面形貌取长度为10 mm的单向预浸带样品,沿纤维轴向撕开表层部分纤维和树脂,制得试样,在试样表面喷金处理后,采用扫描电子显微镜(SEM)(4700型,日立(中国)有限公司)观察纤维表面形貌。
2.3.4 纤维分散均匀度纤维分散均匀度即预浸带中沿纤维径向纤维束的分散情况,可以通过测试预浸带中纤维束厚度的方差来表征。取5片试样,对预浸带截面进行打磨抛光,通过光学显微镜(Leica DM4P型,德国徕卡显微系统CMS有限公司)观察截面,并使用图像处理软件Image-Pro Plus测得均匀分布的10个点的纤维束厚度,如图 10所示。

|
图 10 均匀度测试示意图 Fig.10 Schematic diagram of the uniformity test |
试样的纤维分散均匀度Ef按照式(25)计算,并以5片试样结果的平均值表示。
| $ {E_{\rm{f}}} = \left( {1 - \frac{{{f_{\rm{E}}}}}{h}} \right) \times 100\% $ | (25) |
其中,
| $ {f_{\rm{E}}} = \sqrt {\frac{{\sum\limits_{i = 1}^{10} {{{\left( {{h_{{\rm{E}}i}} - h} \right)}^2}} }}{9}} $ | (26) |
式中,fE为试样的纤维束厚度标准差;hEi为纤维束样本中第i个点的厚度,mm;h为该批试样的平均厚度,mm。
2.3.5 力学性能连续纤维增强预浸带样条的拉伸性能按照ASTM D3039/D3039 M- 14[23]测定。将预浸带模压(保压温度190 ℃,保压时间10 min,保压压力1 MPa)成型,拉伸样条尺寸为250 mm×15 mm×1 mm。采用力学测试仪(RG M- 100A型,瑞格尔仪器有限公司)测试。
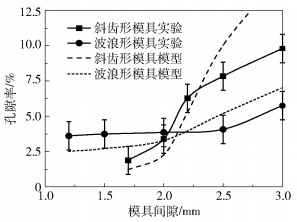
3 结果与讨论 3.1 孔隙率和断裂率图 11和图 12分别为孔隙率和断裂率随模具间隙的变化关系。由结果可知,孔隙率随着模具间隙的增大而增大,纤维断裂率随着模具间隙的增大而减小。模型计算结果与实验结果的变化趋势基本一致,且在大部分模具间隙下二者差距不大,表明本文建立的理论模型可以较好地预测模具的孔隙率和断裂率。
|
图 11 预浸带孔隙率随模具间隙的变化 Fig.11 Variation in prepreg tape porosity with mold gap |
|
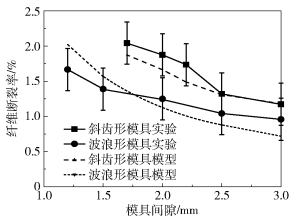
图 12 纤维断裂率随模具间隙的变化 Fig.12 Variation in prepreg tape fracture rate with mold gap |
由图 11可知,当模具间隙小于2 mm时,斜齿形模具制备的预浸带孔隙率比波浪形模具制备的预浸带孔隙率小,这是因为斜齿形模具的楔形结构个数较多,增加了浸渍时间,从而浸渍程度较好。当模具间隙大于2 mm时,波浪形模具制备的预浸带孔隙率更小。当模具间隙大于2.5 mm时,斜齿形模具制备的预浸带的理论孔隙率与实际孔隙率相差很大,主要原因是斜齿形模具的楔形区单元高度较小,可调整的模具间隙较小。当模具间隙大于单元高度时,浸渍楔形区出口高度变得极大,不再为熔体膜状态,使得浸渍压力变化幅度较大,从而理论孔隙率大幅上升。而实验中预浸带在冷却定型过程中由于其孔隙较多,压辊定型造成了纤维内部树脂的二次浸渍,使得实际孔隙率与理论孔隙率有所差距。由图 12可知,斜齿形模具比波浪形模具制备的预浸带纤维断裂率高,其原因是斜齿形模具的流道圆角较小,楔形区个数较多,导致纤维所受应力增大。
3.2 微观形貌分析图 13为两种模具在不同模具间隙下制备的预浸带界面SEM图像。由图可知,波浪形模具制备的预浸带纤维上包覆的树脂量随着模具间隙的变大而减少,在模具间隙为3 mm时纤维基本无明显树脂包覆。斜齿形模具制备的预浸带纤维上包覆的树脂量也随着模具间隙的变大而减少,在间隙为2.5 mm时纤维表面基本无树脂包裹。微观形貌变化规律与前文的孔隙率变化规律基本一致,说明孔隙率的分析结果较准确。

|
图 13 两种模具在不同模具间隙下制备的预浸带界面SEM图 Fig.13 SEM images of the prepreg tapes prepared by the two molds under different mold gaps |
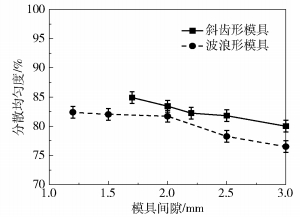
图 14为两种模具制备的单向预浸带的纤维分散均匀度随模具间隙的变化。两种模具下的纤维分散均匀度均随着模具间隙的增大而减小。两模具在各自的最小模具间隙下,斜齿形模具的预浸带有更好的纤维分散效果,波浪形模具的分散均匀度比斜齿形模具低3%左右。斜齿形模具结构的楔形区单元流道圆角结构与预分散机械辊的分散效果相似,可知模具结构中较多的楔形结构个数提高了纤维的分散均匀度。
|
图 14 分散均匀度随模具间隙的变化 Fig.14 Variation in dispersion uniformity of prepreg tape with mold gap |
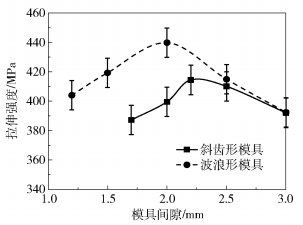
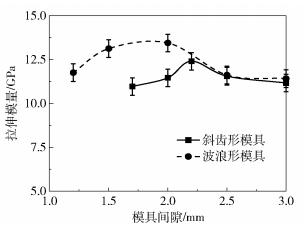
图 15和图 16分别为两种模具制备的单向预浸带的拉伸强度和拉伸模量随模具间隙的变化。从图中可以看出,波浪形模具制备的预浸带的拉伸强度和拉伸模量在模具间隙较小时明显高于斜齿形模具。当预浸带的拉伸性能最优时,斜齿形模具和波浪形模具的模具间隙分别为2.0~2.5 mm和1.5~2.5 mm。
|
图 15 预浸带拉伸强度随模具间隙的变化 Fig.15 Variation in tensile strength of prepreg tape with mold gap |
|
图 16 预浸带拉伸模量随模具间隙的变化 Fig.16 Variation in tensile modulus of prepreg tape with mold gap |
结合孔隙率和断裂率的结果分析,拉伸性能随着孔隙率的增大和断裂率的减小而先增大后减小。当预浸带的孔隙率增大到一定值时,结合SEM微观形貌图易知树脂与纤维之间的结合情况很差,树脂分布变得极不均匀,并且高模具间隙下纤维分散程度更低,则在拉伸过程中力学测试仪对预浸带样品施加拉力时,预浸带中树脂和纤维分布不均使得预浸带所受应力分布不均,导致测得的拉伸性能急剧下降,并且孔隙率较高时模具结构对拉伸性能的影响极小。
综合以上分析和理论模型中各参数的影响,为了制备低孔隙率、低断裂率、高拉伸性能的预浸带,可以结合波浪形模具结构中较大的流道圆角半径、较大的流道单元高度,以及斜齿形模具结构中较多的楔形结构个数来设计优化熔融浸渍模具。
4 结论(1) 孔隙率和断裂率测试结果表明,在大部分模具间隙下实验测试与理论模型计算的结果差距不大,因此本文建立的熔融浸渍模具的纤维浸渍模型和纤维断裂模型能较准确地预测连续纤维增强预浸带的孔隙率和断裂率。
(2) 理论模型计算及实验结果表明,斜齿形模具的楔形区个数较多,流道圆角半径较小,流道单元高度小,模具间隙的可调范围较小,使得其制备的预浸带纤维断裂率高,分散效果好,孔隙率低。波浪形模具的楔型结构个数少,楔形结构长度和流道圆角半径较大,使得其对纤维的分散效果和浸渍效果较差,但纤维断裂率较低,预浸带拉伸性能较高。本文下一步工作将两模具的优点相结合设计浸渍模具,以便制备更高质量的连续纤维增强预浸带。
| [1] |
朱文墨, 李刚, 杨小平, 等. 连续纤维增强树脂复合材料纵向压缩强度预测模型的发展及其影响因素[J]. 复合材料学报, 2020, 37(1): 1-15. ZHU W M, LI G, YANG X P, et al. Development of prediction model and influencing factors of longitudinal compressive strength for continuous fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica, 2020, 37(1): 1-15. (in Chinese) |
| [2] |
宋清华, 肖军, 文立伟, 等. 模压工艺对玻璃纤维增强聚丙烯复合材料层合板力学性能的影响[J]. 复合材料学报, 2016, 33(12): 2740-2748. SONG Q H, XIAO J, WEN L W, et al. Influence of molding press on mechanical properties of glass fiber reinforced polypropylene composite laminates[J]. Acta Materiae Compositae Sinica, 2016, 33(12): 2740-2748. (in Chinese) |
| [3] |
陈丁丁, 王曼漪, 新川和夫, 等. 纤维增强树脂基复合材料拼接结构拉伸性能[J]. 复合材料学报, 2017, 34(11): 2473-2478. CHEN D D, WANG M Y, ARAKAWA K, et al. Tensile properties of fiber reinforced epoxy resin composite with ply splice structures[J]. Acta Materiae Compositae Sinica, 2017, 34(11): 2473-2478. (in Chinese) |
| [4] |
韩振宇, 张鹏, 郑天宇, 等. 纤维增强树脂复合材料网格结构成型工艺研究进展[J]. 复合材料学报, 2020, 37(4): 845-858. HAN Z Y, ZHANG P, ZHENG T Y, et al. Research progress of forming process of fiber reinforced polymer composite grid structure[J]. Acta Materiae Compositae Sinica, 2020, 37(4): 845-858. (in Chinese) |
| [5] |
孙银宝, 李宏福, 张博明. 连续纤维增强热塑性复合材料研发与应用进展[J]. 航空科学技术, 2016, 27(5): 1-7. SUN Y B, LI H F, ZHANG B M. Progress in research and application of continuous fiber reinforced thermoplastic composites[J]. Aeronautical Science and Technology, 2016, 27(5): 1-7. (in Chinese) |
| [6] |
孙正, 刘力源, 刘德博, 等. 纳米改性连续纤维增强热塑性树脂复合材料及其力学性能研究进展[J]. 复合材料学报, 2019, 36(4): 771-783. SUN Z, LIU L Y, LIU D B, et al. Development and mechanical properties of nano-modified continuous fiber reinforced thermoplastic composites[J]. Acta Materiae Compositae Sinica, 2019, 36(4): 771-783. (in Chinese) |
| [7] |
黄达勇, 赵先琼.注塑成型纤维增强热塑性树脂复合材料刚度预测方法[J/OL].复合材料学报.[2021-04-01].https://doi.org/10.13801/j.cnki.fhclxb.20200811.001. HUANG D Y, ZHAO X Q. Stiffness prediction forinjection molded fiber reinforced thermoplastics[J/OL]. Acta Materiae Compositae Sinica.[2021-04-01]. https://doi.org/10.13801/j.cnki.fhclxb.20200811.001. (in Chinese) |
| [8] |
MA Y, JIN S S, UEDA M, et al. Higher performance carbon fiber reinforced thermoplastic composites from thermoplastic prepreg technique: heat and moisture effect[J]. Composites Part B: Engineering, 2018, 154: 90-98. DOI:10.1016/j.compositesb.2018.07.060 |
| [9] |
郝晓霞. LFT浸渍模具及纤维预处理装置的开发及性能研究[D].北京: 北京化工大学, 2018. HAO X X. Design and performance study of LFT impregnation die and fiber pretreatment device[D]. Beijing: Beijing University of Chemical Technology, 2018. (in Chinese) |
| [10] |
孙立坤.连续/长玻璃纤维增强塑性复合材料生产工艺的研究[D].北京: 北京化工大学, 2014. SUN L K. Study on production technology of continuous/long glass fiber reinforced thermoplastic polymer composites[D]. Beijing: Beijing University of Chemical Technology, 2014. (in Chinese) |
| [11] |
孙海青.连续/长纤维增强IPC复合材料的研究[D].淄博: 山东理工大学, 2012. SUN H Q. Study on composites of continuous/long fiber reinforced IPC[D]. Zibo: Shandong University of Technology, 2012. (in Chinese) |
| [12] |
袁满, 何亚东, 李锐, 等. 连续纤维增强热塑性复合材料熔融浸渍模型[J]. 塑料科技, 2019, 47(7): 12-17. YUAN M, HE Y D, LI R, et al. Melt impregnation model of continuous fiber reinforced thermoplastic composites[J]. Plastics Science and Technology, 2019, 47(7): 12-17. (in Chinese) |
| [13] |
KOBAYASHI S, TSUKADA T, MORIMOTO T. Resin impregnation behavior in carbon fiber reinforced polyamide 6 composite: effects of yarn thickness, fabric lamination and sizing agent[J]. Composites Part A: Applied Science and Manufacturing, 2017, 101: 283-289. DOI:10.1016/j.compositesa.2017.06.030 |
| [14] |
STEGGALL-MURPHY C, SIMACEK P, ADVANI S G, et al. A model for thermoplastic melt impregnation of fiber bundles during consolidation of powder-impregnated continuous fiber composites[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41: 93-100. DOI:10.1016/j.compositesa.2009.09.026 |
| [15] |
ǺSTRÖM B T, PIPES R B, ADVANI S G. On flow through aligned fiber beds and its application to composites processing[J]. Journal of Composite Materials, 1992, 26(9): 1351-1373. DOI:10.1177/002199839202600907 |
| [16] |
YAZDCHI K, SRIVASTAVA S, LUDING S. Microstructural effects on the permeability of periodic fibrous porous media[J]. International Journal of Multiphase Flow, 2011, 37(8): 956-966. |
| [17] |
BATES P J, KENDALL J, TAYLOR D, et al. Pressure build-up during melt impregnation[J]. Composites Science and Technology, 2002, 62(3): 379-384. DOI:10.1016/S0266-3538(01)00216-0 |
| [18] |
李莹, 信春玲, 曹敏华, 等. 连续玻纤增强聚丙烯预浸带熔融预浸过程研究[J]. 复合材料学报, 2018, 35(5): 1080-1086. LI Y, XIN C L, CAO M H, et al. Pre-impregnation of continuous glass fiber reinforced polypropylene prepreg[J]. Acta Materiae Compositae Sinica, 2018, 35(5): 1080-1086. (in Chinese) |
| [19] |
张聪.纤维增强热塑性复合材料复合过程中纤维断裂研究[D].北京: 北京化工大学, 2015. ZHANG C. Research on fiber fracture mechanism in the process of continuous fiber reinforced thermoplastic composite[D]. Beijing: Beijing University of Chemical Technology, 2015. (in Chinese) |
| [20] |
李莹.连续玻纤增强聚丙烯预浸带材制备及性能研究[D].北京: 北京化工大学, 2018. LI Y. Research on preparation and properties of continuous glass fiber reinforced polypropylene prepreg tape[D]. Beijing: Beijing University of Chemical Technology, 2018. (in Chinese) |
| [21] |
ASTM International. Standard test methods for void content of reinforced plastics: ASTM D2734-09[S]. West Conshohocken: ASTM International, 2009.
|
| [22] |
张聪, 信春玲, 唐可, 等. 热塑性树脂连续浸渍过程的纤维断裂机制及实验[J]. 复合材料学报, 2015, 32(4): 983-988. ZHANG C, XIN C L, TANG K, et al. Fiber fracture mechanism in process of thermoplastic resincontinuous impregnation and experiments[J]. Acta Materiae Compositae Sinica, 2015, 32(4): 983-988. (in Chinese) |
| [23] |
ASTM International. Standard test method for tensile properties of polymer matrix composite materials: D3039/D3039M-14[S]. West Conshohocken, USA: ASTM International, 2015.
|








