非线性薛定谔方程(NLSE)是一类重要的非线性演化方程,在非线性光学、量子力学、等离子体理论等领域具有广泛的应用,因此研究该类方程的精确解具有重要的理论意义。近年来,人们提出许多求解NLSE精确解的有效方法,如齐次平衡法[1]、tanh函数展开法及其扩展[2]、正弦- 余弦法[2]、exp-函数法[2]、试验函数法及其扩展[3]、扩展辅助方程法[4]、改进的Fan-子方程法[5]、(G′/G)-展开法[6]、exp(-ϕ(ξ))-展开法[6]等。众所周知,经典的NLSE描述了脉冲宽度在100 fs以上的光脉冲在光纤中的传播[7]。随着脉冲宽度逐渐变窄,如接近50 fs甚至低于10 fs时,系统必须考虑非线性项和高阶色散(如三阶和四阶色散)。
本文考虑描述超短光脉冲在光纤中传播的具有高阶色散和立方-五次非线性项的NLSE[8]
| $ \begin{array}{l} \ \ \ \ \ \ \ E_{z}=-\mathrm{i} \frac{\beta_{2}}{2} E_{t t}+\mathrm{i} \gamma_{1}|E|^{2} E+\frac{\beta_{3}}{6} E_{t t t}+\mathrm{i} \frac{\beta_{4}}{24} E_{t t t t}- \\ \mathrm{i} \gamma_{2}|E|^{4} E \end{array} $ | (1) |
式中,E为电场中关于变量z和t的慢变包络,β2=
利用动力系统的分岔理论不仅能够得到方程局部解的表达式,而且还可以探查方程解的整体结构[10-11],因此本文先利用代入法将方程(1)转化为动力系统,再运用分岔理论来分析系统的动力特性。通过分析相图的有界轨道不仅得到了方程有界行波解的显式表达式,而且还可直接获知行波解的分类结构。
1 动力系统分岔分析对方程(1)采用行波变换E(z, t)=φ(ξ)eiη,其中ξ=v0z-vt, η=ω0z-ωt,并分离实部、虚部可得
| $ \begin{array}{l} \left\{\begin{array}{l} l_{3} \varphi^{\prime \prime \prime}(\xi)+l_{1} \varphi^{\prime}(\xi)=0 \\ l_{4} \varphi^{(4)}(\xi)+l_{2} \varphi^{\prime \prime}(\xi)+l_{0} \varphi(\xi)+ \end{array}\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \gamma_{1} \varphi^{3}(\xi)-\gamma_{2} \varphi^{5}(\xi)=0 \end{array} $ | (2) |
式中,
| $ \begin{aligned} &l_{0}=\frac{1}{2} \omega^{2}\left(\beta_{2}+\frac{1}{3} \beta_{3} \omega+\frac{1}{12} \beta_{4} \omega^{2}\right)-\omega_{0} \\ &l_{1}=\omega v\left(\beta_{2}+\frac{1}{2} \beta_{3} \omega+\frac{1}{6} \beta_{4} \omega^{2}\right)-v_{0} \\ &l_{2}=-\frac{1}{2} v^{2}\left(\beta_{2}+\beta_{3} \omega+\frac{1}{2} \beta_{4} \omega^{2}\right) \\ &l_{3}=-\frac{1}{6} v^{3}\left(\beta_{3}+\beta_{4} \omega\right) \\ &l_{4}=\frac{1}{24} \beta_{4} \omega^{4} \end{aligned} $ |
当l1=l3=0时文献[5]采用改进的Fan-子方程法获得对应的行波解;当θ=l2l3-l1l4≠0时将式(2)一式微分并代入式(2)二式中得
| $ \varphi^{\prime \prime}(\xi)=c_{2} \varphi(\xi)+2 c_{4} \varphi^{3}(\xi)+3 c_{6} \varphi^{5}(\xi) $ | (3) |
式中,c2=-l0l3/θ, 2c4=-γ1l3/θ, 3c6=γ2l3/θ。式(3)等价于如下所示的二维自治系统
| $ \left\{\begin{array}{l} \frac{\mathrm{d} \varphi}{\mathrm{d} \xi}=y \\ \frac{\mathrm{d} y}{\mathrm{~d} \xi}=c_{2} \varphi+2 c_{4} \varphi^{3}+3 c_{6} \varphi^{5} \end{array}\right. $ | (4) |
这是一个具有Hamilton函数
| $ H(\varphi, y)=y^{2}-c_{2} \varphi^{2}-c_{4} \varphi^{4}-c_{6} \varphi^{6}=h $ |
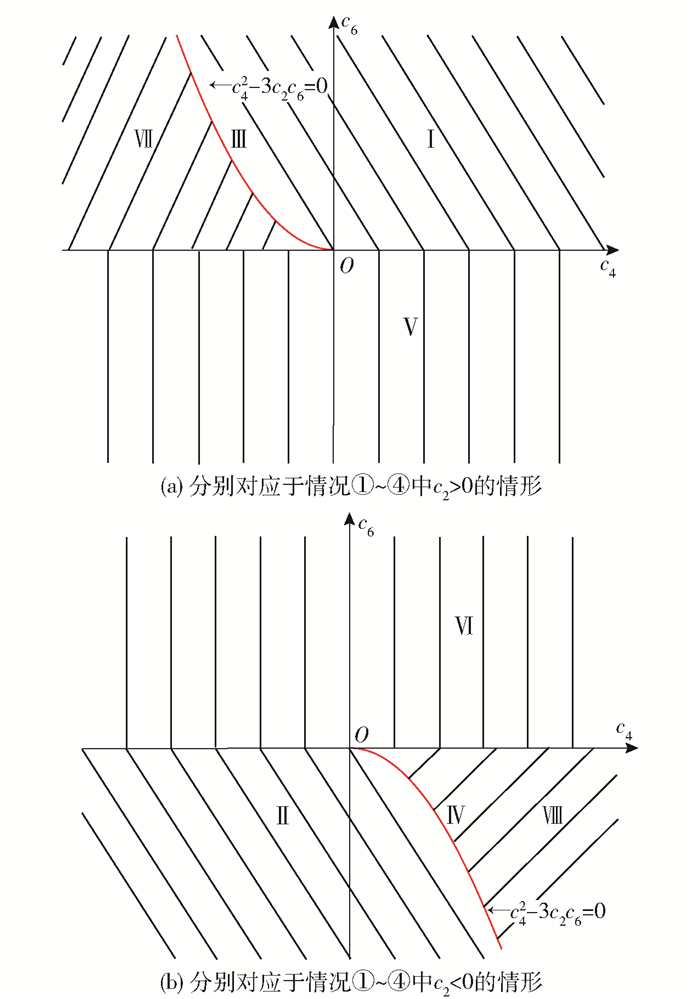
的可积系统。根据Δ=c42-3c2c6以及各系数的正、负平衡点的个数及类型可分为区域Ⅰ~Ⅷ 8种情况,如图 1所示。下面将c2>0和c2 < 0合并到一起,共分为4类情况进行介绍。
|
图 1 平衡点个数及其类型的分布区域 Fig.1 The distribution regions of the number and type of equilibrium points |
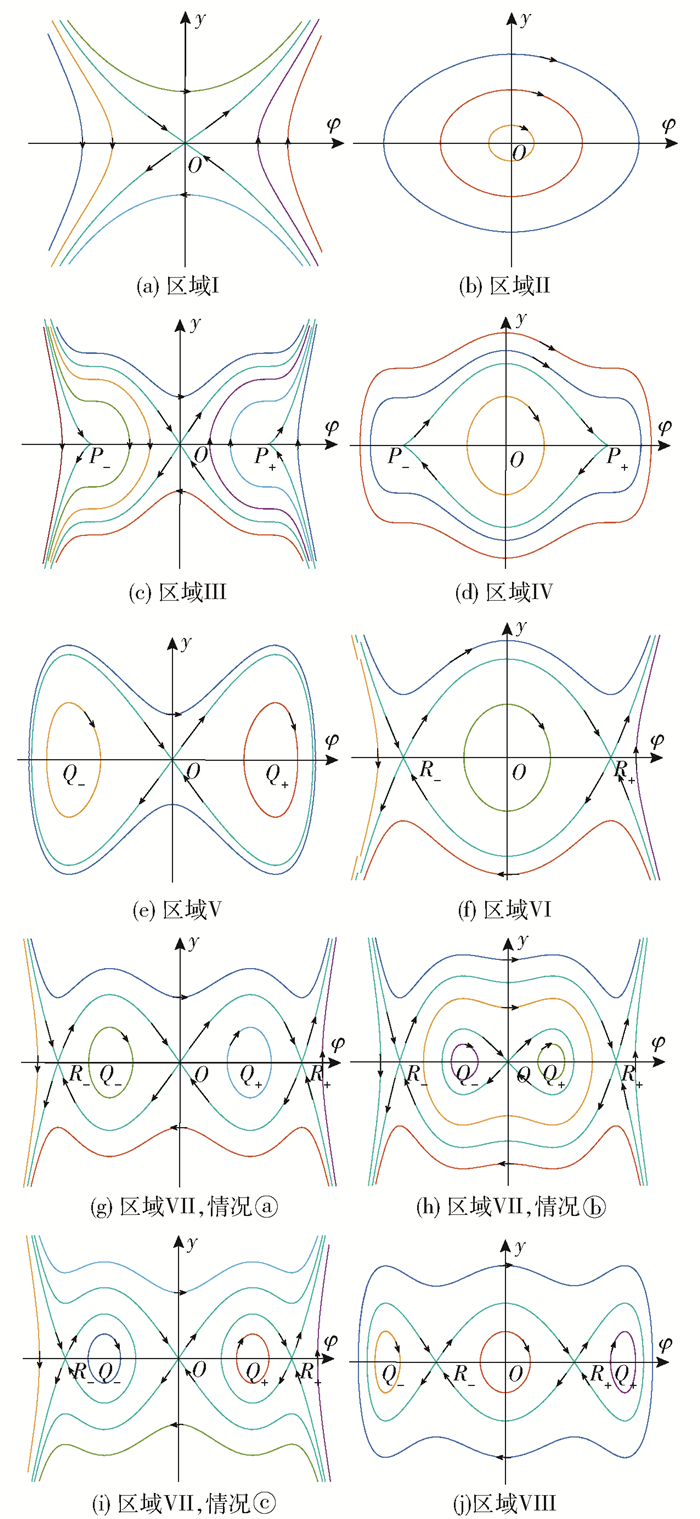
① 当c42 < 3c2c6,或当c42≥3c2c6且c4c6>0时,系统(4)只有1个平衡点O(0, 0)。c2、c4、c6均为正时(区域Ⅰ)O是鞍点(图 2(a));c2、c4、c6均为负时(区域Ⅱ)O是中心点(图 2(b))。
|
图 2 不同区域所对应的相图 Fig.2 Phase diagrams for different regions |
② 当c42=3c2c6, c4c6 < 0时,系统(4)有3个平衡点,即O(0, 0),
③ 当c2c6 < 0时,系统(4)有3个平衡点,即O(0, 0),Q±(φ1±, 0)或R±(φ2±, 0)。c2>0时(区域Ⅴ)O是鞍点,Q±是中心点(图 2(e));c2 < 0时(区域Ⅵ)O是中心点,R±是鞍点(图 2(f))。其中,
④ 当c42>3c2c6>0, c4c6 < 0时,系统(4)有5个平衡点,即O(0, 0)、Q±(φ1±, 0)和R±(φ2±, 0)。当c2>0时(区域Ⅶ)O、R±是鞍点,Q±是中心点,此时分为3种情况:ⓐ在c42=4c2c6时,有H(Q±) < H(R±)=H(O)(图 2(g));ⓑ在c42>4c2c6时,有H(Q±) < H(O) < H(R±)(图 2(h));ⓒ在c42 < 4c2c6时,有H(Q±) < H(R±) < H(O)(图 2(i))。当c2 < 0时(区域Ⅷ)O、Q±是中心点,R±是鞍点(图 2(j))。
2 NLSE的精确解对于一个固定的h∈R,曲线
| $ C_{h}=\{(\varphi, y) \in R \times R: H(\varphi, y)=h\} $ |
被称为具有h能量水平的能量曲线[12]。显然,H(φ, y)=h的每个轨道都是一条能量曲线,因此可以研究其有界轨道与能量水平h之间的关系。设
| $ F_{h}(\varphi)=h+c_{2} \varphi^{2}+c_{4} \varphi^{4}+c_{6} \varphi^{6} $ |
显然能量曲线Ch相当于y2=Fh(φ)所定义的曲线,标记H(Q±)=h1=-F0(φ1±),H(R±)=h2= -F0(φ2±)。下面将通过分析情况③~④所对应能量h的变化来得到系统精确解的分类及分布。
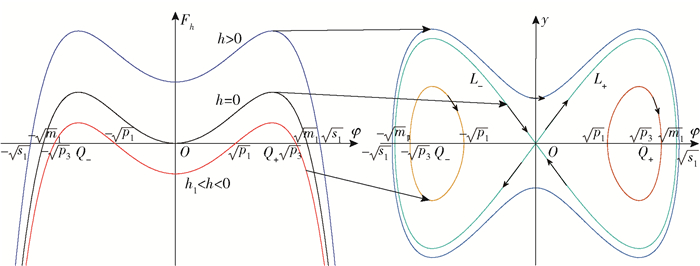
2.1 区域Ⅴ对应系统的精确解此时c42>3c2c6, c2>0, c6 < 0且h1 < 0,能量曲线与相图中各有界轨道的对应关系如图 3所示。
|
图 3 c42>3c2c6, c2>0, c6 < 0时能量曲线与相图的对应关系 Fig.3 Correspondence between the energy curve and phase diagram at c42>3c2c6, c2>0, c6 < 0 |
根据能量水平h范围的不同,分为如下3种情况。
1) h=0时,这是一条连接鞍点O的稳定流形和不稳定流形的同宿轨
| $ y=\pm \sqrt{-c_{6} \varphi^{2}\left(m_{1}-\varphi^{2}\right)\left(\varphi^{2}-m_{2}\right)} $ |
式中,
| $ \begin{array}{l} \ \ \ \ \ \ \ \ E_{1 \pm}(z, t)= \\ \pm\left[\frac{-m_{1} m_{2}}{\left(m_{1}-m_{2}\right) \sinh ^{2} \sqrt{c_{6} m_{1} m_{2} }\xi-m_{2}}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i\eta}} \end{array} $ | (5) |
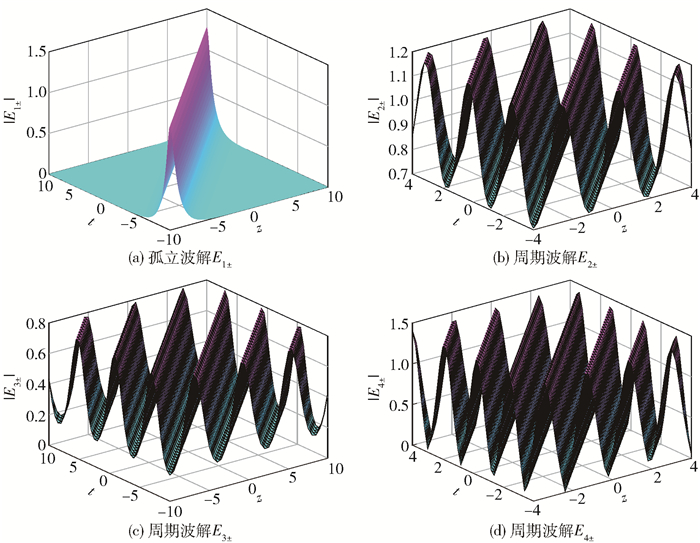
其分别对应于左半平面的同宿轨道族L-(O, O)和右半平面的同宿轨道族L+(O, O),波形图如图 4(a)所示。
|
图 4 孤立波解E1±和周期波解E2±、E3±、E4±的三维波形图 Fig.4 The three-dimensional waveform of the solitary wave solution E1± and periodic wave solutions E2±, E3±, E4± |
2) h∈(h1, 0)时,这是位于同宿轨内部,分别围绕中心点Q±的两个周期轨
| $ y=\pm \sqrt{-c_{6}\left(\varphi^{2}-p_{1}\right)\left(\varphi^{2}-p_{2}\right)\left(p_{3}-\varphi^{2}\right)} $ |
式中,0 < p1 < φ1±2,
| $ E_{2 \pm}(z, t)=\pm\left[\frac{p_{1} p_{3}}{p_{1}+\left(p_{3}-p_{1}\right) \operatorname{cn}^{2}\left(d_{1} \xi, k_{1}\right)}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (6) |
式中,
3) h>0时,这是位于同宿轨外部,包围平衡点O和Q±在内的一个周期轨。当m1 < s1 < (-c4-2
| $ E_{3 \pm}(z, t)=\pm\left[\frac{s_{2} s_{3}}{s_{2}+\left(s_{3}-s_{2}\right) \operatorname{sn}^{2}\left(d_{2} \xi, k_{2}\right)}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (7) |
式中,
当s1>(-c4-2
| $ E_{4 \pm}(z, t)=\pm\left[\frac{s_{1} \sqrt{s_{5}} \operatorname{cn}\left(2 d_{3} \xi, k_{3}\right)+s_{1} \sqrt{s_{5}}}{e_{1}+e_{2} \operatorname{cn}\left(2 d_{3} \xi, k_{3}\right)}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (8) |
式中,s4=s1+c4/c6,s5=s12+c4s1/c6+c2/c6,e1, 2=
此时c42>3c2c6, c2 < 0, c6>0且h2>0,能量曲线与相图中各轨道的对应关系如图 5所示。
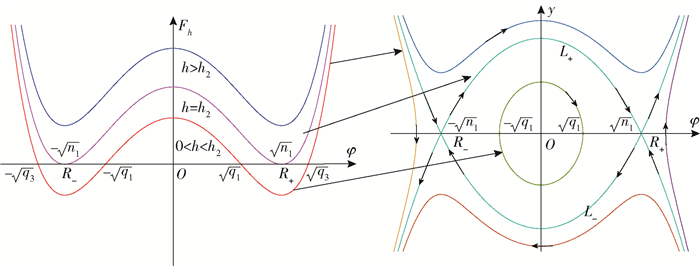
|
图 5 c42-3c2c6>0, c2 < 0, c6>0时能量曲线与相图对应关系 Fig.5 Correspondence between the energy curve and phase diagram at c42-3c2c6>0, c2 < 0, c6>0 |
根据能量水平h范围的不同,分为如下两种情况。
1) h=h2时,这是一条连接鞍点R±的稳定流形和不稳定流形的异宿轨
| $ y=\pm \sqrt{c_{6}\left(n_{1}-\varphi^{2}\right)^{2}\left(\varphi^{2}-n_{2}\right)} $ |
式中,
| $ \begin{array}{l} \ \ \ \ \ \ \ \ E_{5 \pm}(z, t)= \\ \pm\left[\frac{-n_{1} n_{2} \sinh ^{2}\left(\xi \sqrt{c_{6} n_{1}\left(n_{1}-n_{2}\right)}\right)}{n_{1}-n_{2} \cosh ^{2}\left(\xi \sqrt{c_{6} n_{1}\left(n_{1}-n_{2}\right)}\right)}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} \end{array} $ | (9) |
分别对应于异宿轨道族L-(R+, R-)和L+(R-, R+),波形图如图 6(a)所示。
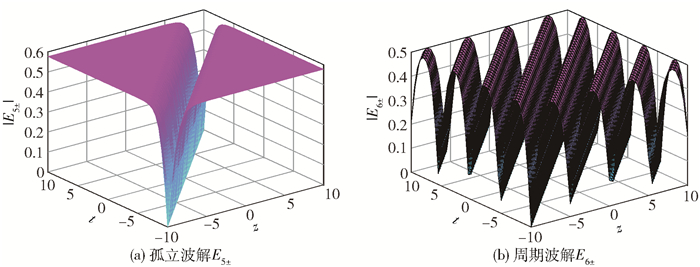
|
图 6 孤立波解E5±和周期波解E6±的三维波形图 Fig.6 The three-dimensional waveforms of the solitary wave solution E5±and periodic wave solution E6± |
2) h∈(0, h2)时,这是位于异宿轨内部,包围中心点O的一个周期轨
| $ y=\pm \sqrt{c_{6}\left(q_{1}-\varphi^{2}\right)\left(\varphi^{2}-q_{2}\right)\left(q_{3}-\varphi^{2}\right)} $ |
式中,0 < q1 < n1,
| $ E_{6 \pm}(z, t)=\pm\left[\frac{-q_{1} q_{2} \operatorname{sn}^{2}\left(d_{4} \xi, k_{4}\right)}{q_{1} c n^{2}\left(d_{4} \xi, k_{4}\right)-q_{2}}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (10) |
式中,
此时c2>0, c4 < 0, c6>0, c42=4c2c6且h1 < h2=0,能量曲线与相图中各轨道的对应关系如图 7所示。
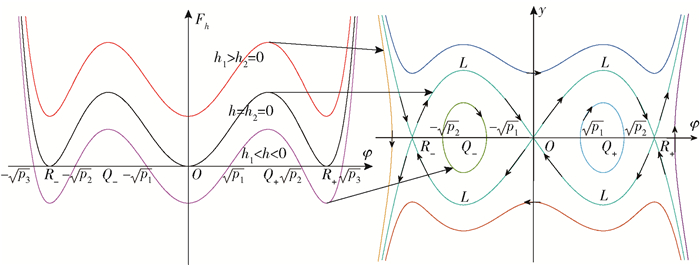
|
图 7 c2>0, c4 < 0, c6>0, c42=4c2c6时能量曲线与相图对应关系 Fig.7 Correspondence between the energy curve and phase diagram at c2>0, c4 < 0, c6>0, c42=4c2c6 |
根据能量水平h范围的不同,分为如下两种情况。
1) h=h2=0时,这是一条连接鞍点O和R±的稳定流形和不稳定流形的异宿轨
| $ y=\pm \sqrt{c_{6} \varphi^{2}\left(\varphi^{2}+\frac{c_{4}}{2 c_{6}}\right)^{2}} $ |
因此得到扭结波解为
| $ E_{7{\pm}}(z, t)=\pm\left\{-\frac{c_{4}}{4 c_{6}}\left[1 \pm \tanh \left(\xi \sqrt{c_{2}}\right)\right]\right\}^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (11) |
分别对应于异宿轨道族L(O→R+→O)和L(O→R-→O),波形图如图 8所示。
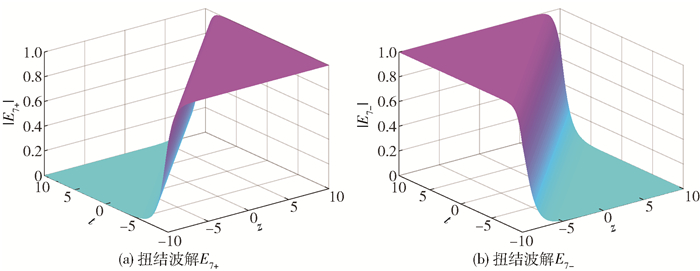
|
图 8 扭结波解E7±的三维波形图 Fig.8 The three-dimensional waveform of the kink wave solution E7± |
2) h∈(h1, 0)时,这是位于同宿轨内部分别围绕中心点Q±的两个周期轨。因此周期波解为
| $ E_{8 \pm}(z, t)=\pm\left[\frac{p_{1} p_{2}}{p_{1}+\left(p_{2}-p_{1}\right) \operatorname{cn}^{2}\left(d_{5} \xi, k_{5}\right)}\right]^{\frac{1}{2}} \mathrm{e}^{\mathrm{i} \eta} $ | (12) |
式中,
本文对图 2中区域Ⅶ的情况ⓑ、ⓒ及区域Ⅷ分别对应的3个相图也进行了与前面类似的讨论,得到对应的周期波解和孤立波解,并且发现其对应的波形无太大差别,在此不再赘述。
3 结论本文研究了描述超短光脉冲在光纤中传播的具有高阶色散和立方- 五次非线性项的薛定谔方程的精确解。采用代入法和动力系统的分岔理论得到方程的10个相图,对其中比较典型的3个相图进行理论分析,找到了系统的孤立波解、扭结波解和周期波解等精确解,并进行了数值验证,给出了波形的三维图。孤立波解的存在意味着非线性和色散之间的完美平衡,我们给出了孤立波解的存在条件,从而也证实了该系统所描述的光纤在一定条件下能够稳定地进行长时传播。同时本文对系统动态分析的结果体现了行波结构的多样性和完整性。
| [1] |
TAGHIZADEH N, MIRZAZADEH M, MAHMOODIRAD A. Application of Kudryashov method for high-order nonlinear Schrödinger equation[J]. Indian Journal of Physics, 2013, 87(8): 781-785. DOI:10.1007/s12648-013-0296-2 |
| [2] |
MOGHADDAM M Y, ASGARI A, YAZDANI H. Exact travelling wave solutions for the generalized nonlinear Schrödinger (GNLS) equation with a source by extended tanh-coth, sine-cosine and exp-function methods[J]. Applied Mathematics and Computation, 2009, 210(2): 422-435. DOI:10.1016/j.amc.2009.01.002 |
| [3] |
CAO R, ZHANG J. Trial function method and exact solutions to the generalized nonlinear Schrödinger equation with time-dependent coefficient[J]. Chinese Physics B, 2013, 22(10): 100507. DOI:10.1088/1674-1056/22/10/100507 |
| [4] |
AZZOUZI F, TRIKI H, MEZGHICHE K, et al. Solitary wave solutions for high dispersive cubic-quintic nonlinear Schrödinger equation[J]. Chaos, Solitons and Fractals, 2009, 39(3): 1304-1307. DOI:10.1016/j.chaos.2007.06.024 |
| [5] |
XIE Y A, TANG S Q. New exact solutions for high dispersive cubic-quintic nonlinear Schrödinger equation[J]. Journal of Applied Mathematics, 2014, 2014: 826746. |
| [6] |
ZAYED E M E, AMER Y A, SHOHIB R M A. The (G'/G)-expansion method and the exp(-φ(ξ))-expansion method with applications to a higher order dispersive nonlinear Schrödinger equation[J]. Scientific Research and Essays, 2015, 10(6): 218-231. DOI:10.5897/SRE2015.6196 |
| [7] |
ILHAN O A, ESEN A, BULUT H, et al. Singular solitons in the pseudo-parabolic model arising in nonlinear surface waves[J]. Results in Physics, 2019, 12: 1712-1715. DOI:10.1016/j.rinp.2019.01.059 |
| [8] |
HASEGAWA A, TAPPERT F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. Ⅰ. anomalous dispersion[J]. Applied Physics Letters, 1973, 23(3): 142-144. DOI:10.1063/1.1654836 |
| [9] |
TANEV S, PUSHKAROV D I. Solitary wave propagation and bistability in the normal dispersion region of highly nonlinear optical fibres and waveguides[J]. Optics Communications, 1997, 141(5/6): 322-328. |
| [10] |
LI Y, SHAN W R, SHUAI T P, et al. Bifurcation analysis and solutions of a higher-order nonlinear Schrödinger equation[J]. Mathematical Problems in Engineering, 2015, 2015: 408586. |
| [11] |
DU L X, SUN Y H, WU D S. Bifurcations and solutions for the generalized nonlinear Schrödinger equation[J]. Physics Letters A, 2019, 383(36): 126028. DOI:10.1016/j.physleta.2019.126028 |
| [12] |
LI J B, DAI H H. On the study of singular nonlinear traveling wave equations: dynamical system approach[M]. Beijing: Science Press, 2007: 21-23.
|








