引言

线性混合效应模型是处理纵向数据最主要的模型之一，Diggle等^[1]首次基于线性混合模型详细地研究了针对纵向数据的统计分析方法。随着纵向数据研究的不断发展，线性混合模型在生物、医学、卫生、心理学、农学和经济学等各个领域都有了非常广泛的应用。

影响分析作为统计建模中非常重要的一部分，主要被应用于识别数据中的强影响点和异常值点。近年来，关于线性混合模型的影响分析问题已经成为了研究热点之一。例如，当总体误差服从正态分布时，Pan等^[2]基于似然函数及其导出的Q函数研究了线性混合模型在不同的随机效应协方差结构下的影响诊断问题；当模型误差服从指数族分布时，Xu等^[3]基于数据删除模型对广义线性混合效应模型进行影响分析，基于似然函数关于随机效应的条件期望构造了Q函数，进而建立了广义Cook距离和似然距离等；Pinho等^[4]考虑了广义线性混合模型不同参数的影响分析问题，并且基于固定效应和随机效应估计的联合影响构建了广义Cook距离。此外，孙慧慧等^[5]与Tang等^[6]还分别研究了线性混合模型和部分线性混合模型的局部影响分析问题。然而，在很多情况下纵向数据模型的误差可能服从非正态分布或者非对称分布，此时一般的估计精度很容易受到影响^[4]。分位数回归估计作为一种稳健的估计方法，不仅可以克服上述问题，并且能够获得数据的总体分布信息，尤其是当回归误差项服从重尾分布或其分布受到污染时，分位数回归估计具有更高的稳健性。

Koenker^[7]最早对混合效应模型的分位数估计方法进行了研究，他利用加权分位数和对随机效应进行L1惩罚的方式，给出了模型的损失函数，获得了模型系数和随机效应的分位数估计。Geraci等^[8]利用Monte Carlo expectation maximization(MCEM)算法消除了随机效应的影响，并求解了线性混合模型系数的分位数估计。尽管分位数回归估计具有稳健性，但是Narula等^[9]的研究表明，在分位数τ较大或者较小的情况下，估计结果也会受到极端异常点的影响，此外他们的数值模拟结果和实际数据分析也说明了针对最小绝对偏差(least absolute deviation，LAD)回归进行影响分析等的统计诊断技术对异常数据的检测是非常重要的。尽管目前已经有很多关于影响分析的研究，但由于计算及统计推断的复杂性，针对线性混合效应模型分位数估计的影响分析的文献还很少见到，因此基于线性混合效应模型分位数估计对强影响点的诊断度量和异常值的检测进行研究是十分必要的。

本文利用线性混合效应模型的分位数估计处理服从非对称、非正态，尤其是重尾或轻尾分布的纵向数据模型的影响分析问题。为了检验强影响点并减少计算量，通过对分位数回归的光滑逼近得到了数据删除模型参数的一步近似估计，并构造了检验强影响点的损失函数距离和Cook距离。在识别异常值时，首先证明了数据删除模型和均值漂移模型参数估计的等价性，然后基于参数等价性给出计算Wald统计量的方法，并利用Bootstrap方法得到异常值检验的拒绝域。

1 实验数据描述及线性混合模型 1.1 数据描述

为了对氨基羟基脲(HSC)水溶液及硝酸水溶液在γ射线作用下的辐解产物进定量分析，考察不同辐解剂量、HSC初始浓度以及硝酸浓度条件下主要辐解产物的生成量，分别配制浓度为0.1、0.2、0.4、0.6、0.8、1.0 mol/L的HSC溶液和浓度为0.2、0.4、0.6、0.8、1.0、1.5 mol/L的硝酸溶液，两两组合得到36种不同浓度配比的溶液，委托中国原子能科学研究院辐照中心，采用实验型钴源装置(⁶⁰Co源装置)，分别置于辐解剂量为1×10³、2×10³、4×10³、6×10³、8×10³、10×10³ Gy的条件下，进行三因素下的无重复实验，总共得到216个样品。

为了考察不同条件下辐解剂量(10³ Gy)、HSC初始浓度(mol/L)以及硝酸浓度(mol/L)对铵根离子浓度(mmol/L)变化情况的影响，首先对数据进行初步的相关分析和散点图对比，结果表明辐解剂量与铵根离子浓度大体呈线性关系，而单独的HSC初始浓度和硝酸浓度对铵根离子浓度的影响则无明显的趋势变化规律。因此，本文将辐解剂量作为重要的解释变量，而将硝酸浓度和HSC浓度的联合影响作为铵根离子浓度的随机影响因素，建立线性混合效应模型，分别考察两个因素的影响大小。

1.2 线性混合模型及其分位数估计

设y_ij为第i组实验第j次观测记录的铵根离子浓度，i=1, 2，…, n代表HSC初始浓度和硝酸浓度的不同取值的组合，j=1, 2，…, n_i代表在这些不同取值组合下的观测数，总样本数$N=\sum\limits_{i=1}^{n} n_{i}$。假设y_ij服从如式(1)所示的一类线性混合效应模型

$ y_{i j}=\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}+b_{i}+{\varepsilon}_{i j} $

(1)

式中，x_ij=(x_ij1, x_ij2, …, x_ijp)^T是p×1维的与固定效应相关的重要回归变量，β是p×1维的固定效应向量，b_i~N(0, σ_b²I)是不可观测的随机效应，ε_ij~N(0, σ_ε²I)是相互独立的均值为零的随机误差，σ_b²I和σ_ε²I分别是协方差，并且ε_ij与b_i相互独立。混合效应模型假定模型扰动项由两部分组成，一部分随观测时间同时也随个体而变化，另一部分只随个体而不随观测时间变化。引入随机效应可以使个体观测数据之间具有一定的相关性。由于随机效应b_i是彼此相互独立的，因此当将随机效应和模型误差合在一起看作是模型的扰动时，二者共同刻画了纵向数据的组间独立性和组内相关性。

由于很多化学实验数据通常服从非对称、非正态的概率分布，为了克服误差分布的影响，采用稳健的分位数估计方法。根据Koenker^[7]的定义，在τ分位数下的线性混合模型具有如下形式

$ \begin{array}{l} \ \ \ \ \ \ \ \ Q_{y_{i j}}\left(\tau \mid \boldsymbol{x}_{i j}\right)=\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}(\boldsymbol{\tau})+b_{i}, i=1,2, \cdots, n, j=1,2, \\ \cdots, n_{i} \end{array} $

(2)

式中，Q_yij(·)=F^－1_yij(·)是y_ij的条件累积分布函数的逆，分位数τ∈(0，1)，β(τ)是τ分位数下模型的固定效应，b_i是不依赖分位数τ的随机效应。

为了解决估计随机效应时可能会面临的维数较高的问题，Koenker^[7]提出一种基于随机效应的L1惩罚方法，通过加权多个分位数下的信息来获取参数与随机效应的联合估计，其损失函数定义如下

$ \begin{array}{l} \ \ \ \ \ \ \ \ L(\boldsymbol{\beta}, \boldsymbol{b})=\sum\limits_{k=1}^{q} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n_{i}} w_{h} \rho_{\tau_{k}}\left(y_{i j}-b_{i}-\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}\left(\tau_{k}\right)\right)+ \\ \lambda \sum\limits_{i=1}^{n}\left|b_{i}\right| \end{array} $

(3)

式中，ρ_τ(r)=rτI(r>0)+r(τ－1)I(r < 0)，q是分位数个数，w_k是第k个分位数的权重，λ是惩罚因子。Koenker^[7]建议将惩罚因子λ设置为λ=σ_ε/σ_b，其中σ_ε和σ_b可通过计算软件进行求解，具体选取过程详见第3节。

由文献[7]可知，由于随机效应服从零均值的正态分布，为了保证固定效应的估计量具有较好的统计性质，要求固定效应中必须包含截距项。通过极小化损失函数(式(3))获得的参数估计记为$\mathit{\boldsymbol{\widehat \eta }} = {\left({\mathit{\boldsymbol{\widehat \beta }}, \mathit{\boldsymbol{\widehat b}}} \right)^{\rm{T}}}$。为求解损失函数的极小化解，以往的学者们提出了不同的求解思想和算法。其中，Koenker^[7]将问题转化为线性规划问题，然后利用单纯形法或内点法等优化算法进行计算。针对式(3)的损失函数，R语言提供了regression quantiles for panel data (RQPD)程序包用于求解纵向数据的分位数估计。

2 线性混合效应模型分位数估计的影响分析

实际数据中常常会存在一些异常数据，通常将对回归估计影响过大的数据点称为强影响点，而将偏离回归直线较远的点称为异常值点。有时强影响点也很有可能同时是异常值点。影响分析正是为了识别出这些数据点而发展起来的一个统计分支，影响分析中常用的诊断模型包括数据删除模型(case deletion model，CDM)和均值漂移模型(mean shift outlier model，MSOM)。

2.1 数据删除模型的影响分析 2.1.1 数据删除模型

数据删除模型主要通过依次删除每个数据点来求解参数，之后再对比各个参数估计，若数据中存在较强的影响点，那么当删除该点时，模型的参数估计相对于原估计就会有较大的变化。

假定删去第(i₁, j₁)个观测值时得到的模型为

$ \begin{array}{l} \ \ \ \ \ \ \ \ y_{i j}=\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}+b_{i}+\varepsilon_{i j}, i=1,2 \cdots n, j=1,2, \cdots, n_{i}, ( i ,\\ j) \neq\left(i_{1}, j_{1}\right) \end{array} $

(4)

则模型(4)的参数估计记为${\mathit{\boldsymbol{\widehat \eta }}_{\left[{{i_1}{j_1}} \right]}} = {\left({{{\mathit{\boldsymbol{\widehat \beta }}}_{\left[{{i_1}{j_1}} \right]}}, {{\mathit{\boldsymbol{\widehat b}}}_{\left[{{i_1}{j_1}} \right]}}} \right)^{\rm{T}}}$。

2.1.2 参数一步(光滑)近似估计

模型(4)相较原模型(1)只是减少了1个数据，所以参数估计的方法及计算复杂度与原模型基本相同，但是当数据量很大时，由于需要逐一检验每个数据点，将会产生很大的计算负担。针对线性模型，Cook等^[10]提出了利用似然函数的Taylor展开式构造参数近似估计的思想。

为了能够对不可导的损失函数(3)进行光滑逼近，以建立数据删除模型参数的一步近似估计，本文结合一般分位数参数估计的minorize-maximization(MM)算法^[11]和绝对值函数的光滑方法^[12]，构造如下目标函数

$ \begin{array}{l} \ \ \ \ \ \ \ \ M(\boldsymbol{r}, \boldsymbol{b} \mid \hat{\boldsymbol{r}})=\sum\limits_{k=1}^{q} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n_{i}} w_{k} \frac{1}{4}\left(\frac{r_{k i j}^{2}}{\delta+\left|\hat{r}_{k i j}\right|}+\left(4 \tau_{k}-\right.\right. \\ \left.2) r_{k i j}+C_{k}\right)+\lambda \sum\limits_{i=1}^{n} \mu \ln \left(\mathrm{e}^{\frac{b_{i}}{\mu}}+\mathrm{e}^{\frac{-b_{i}}{\mu}}\right) \end{array} $

(5)

式中，r_kij=y_ij－x_ij^Tβ(τ_k)－b_i，δ>0、μ>0是接近零的正常数，C_k是常数。对数据删除模型目标函数在$\mathit{\boldsymbol{\widehat \eta }} = {\left({\mathit{\boldsymbol{\widehat \beta }}, \mathit{\boldsymbol{\widehat b}}} \right)^{\rm{T}}}$处进行Taylor展开得

$ \begin{array}{l} \ \ \ \ \ \ \ \ M_{\left[i_{1} j_{1}\right]}\left(\boldsymbol{\eta}_{\left[i_{1}j_{1}\right]} \mid \hat{\boldsymbol{r}}_{\left[i_{1}j_{1}\right]}\right)=M_{\left[i_{1} j_{1}\right]}\left(\hat{\boldsymbol{\eta}} \mid \hat{\boldsymbol{r}}_{\left[i_{1} j_{1}\right]}\right)+ \\ \left(\boldsymbol{\eta}_{\left[i_{1}j_{1}\right]}-\hat{\boldsymbol{\eta}}\right)^{\mathrm{T}} M_{\left[i_{1} j_{1}\right]}^{\prime}\left(\hat{\boldsymbol{\eta}} \mid \hat{\boldsymbol{r}}_{\left[i_{1} j_{1}\right]}\right)+\left(\boldsymbol{\eta}_{\left[i_{1} j_{1}\right]}-\hat{\boldsymbol{\eta}}\right)^{\mathrm{T}} \\ \frac{M_{\left[i_{1} j_{1}\right]}^{\prime \prime}\left(\hat{\boldsymbol{\eta}} \mid \hat{\boldsymbol{r}}_{\left[i_{1} j_{1}\right]}\right)}{2}\left(\boldsymbol{\eta}_{\left[i_{1} j_{1}\right]}-\hat{\boldsymbol{\eta}}\right)+o(1) \end{array} $

(6)

对式(6)两端关于${\mathit{\boldsymbol{\eta }}_{\left[{{i_1}{j_1}} \right]}}$求导可得^[10]

$ \begin{array}{l} \ \ \ \ \ \ \ \ \hat{\boldsymbol{\eta}}_{\left[i_{1} j_{1}\right]} \approx \hat{\boldsymbol{\eta}}-\left[M_{\left[i_{1} j_{1}\right]}^{\prime \prime}\left(\hat{\boldsymbol{\eta}} \mid \hat{r}_{\left[i_{1} j_{1}\right]}\right)\right]^{-1} M_{\left[i_{1}{1}_{1}\right]}^{\prime}(\hat{\boldsymbol{\eta}} \mid \\ \left.\hat{r}_{\left[i_{1} j_{1}\right]}\right) \end{array} $

(7)

2.1.3 诊断度量

通常情况下，参数估计都是多维向量，不便于直接比较，所以需要通过构建诊断度量来衡量参数变化的大小。在普通的回归模型中，常用的诊断度量有似然距离和Cook距离等，本文将似然距离推广到基于损失函数的距离。

1) 根据损失函数(3)，构建基于损失函数的距离

$ L_{\mathrm{D}}=2\left[L(\hat{\boldsymbol{\beta}}, \hat{\boldsymbol{b}})-L_{\left[i_{1} j_{1}\right]}\left(\hat{\boldsymbol{\beta}}_{\left[i_{1}j_{1}\right]}, \hat{\boldsymbol{b}}_{\left[i_{1} j_{1}\right]}\right)\right] $

(8)

式中，L_[i1j1]$\left({{{\mathit{\boldsymbol{\widehat \beta }}}_{\left[{{i_1}{j_1}} \right]}}, {{\mathit{\boldsymbol{\widehat b}}}_{\left[{{i_1}{j_1}} \right]}}} \right)$是删去第(i₁, j₁)个观测值的数据删除模型的损失函数。该距离类似于似然距离，但是使用的目标函数不同。另外针对损失函数(3)中的权重选取，可以利用损失函数距离(8)分别研究数据在不同分位数下的情况。

2) Cook距离定义为^[10]

$ L_{\mathrm{CD}}=\left(\hat{\boldsymbol{\eta}}_{\left[i_{1}j_{1}\right]}-\hat{\boldsymbol{\eta}}\right)^{\mathrm{T}}[\operatorname{Var}(\hat{\boldsymbol{\eta}})]^{-1}\left(\hat{\boldsymbol{\eta}}_{\left[i_{1}{j}_{1}\right]}-\hat{\boldsymbol{\eta}}\right) / p $

(9)

式中p为参数η的维数。由于没有对模型(2)的误差项作任何的分布假定，所以在中小样本的情况下很难求得Cook距离中的Var($\mathit{\boldsymbol{\widehat \eta }}$)。为了解决此问题，本文在中小样本条件下采用Bootstrap方法来近似计算样本方差Var($\mathit{\boldsymbol{\widehat \eta }}$)。文献[7]中介绍了在τ分位数下构建Bootstrap样本的抽样方法，但是由于本文采用的加权分位数可以同时用于多个分位数下的参数估计，因此本文抽样误差需要从τ=0.5时的分位数下产生，具体操作步骤如下。

1) 利用容量为N的原始样本求解分位数参数估计$\mathit{\boldsymbol{\widehat \eta }} = {\left({\mathit{\boldsymbol{\widehat \beta }}, \mathit{\boldsymbol{\widehat b}}} \right)^{\rm{T}}}$。假设共有q个分位数，则记$\mathit{\boldsymbol{\widehat \beta }}\left({{\tau _{q/2}}} \right)$为τ=0.5分位数下的参数估计，利用${\widehat \varepsilon _{ij}} = {y_{ij}} - \mathit{\boldsymbol{x}}_{ij}^{\rm{T}}\mathit{\boldsymbol{\widehat \beta }}\left({{\tau _{q/2}}} \right) - {{\hat b}_i}$生成残差集合{${\widehat \varepsilon _{ij}}$}。

2) 从残差集合{${\widehat \varepsilon _{ij}}$}中有放回地随机抽取一个容量为N的Bootstrap残差集合{$\widehat \varepsilon _{ij}^*$}。

3)利用$y_{i j}^{*}=\boldsymbol{x}_{i j}^{\mathrm{T}} \hat{\boldsymbol{\beta}}\left(\tau_{q / 2}\right)+\hat{b}_{i}+\hat{\varepsilon}_{i j}^{*}$生成Bootstrap样本(x, y^*)_ij。

4) 利用Bootstrap样本(x, y^*)_ij求解多个分位数下的参数估计$\mathit{\boldsymbol{\widehat \eta }}_{{\tau _k}ij}^*$。

5) 重复步骤2)至步骤4)共M次，记τ_k分位数下的参数估计$\hat{\boldsymbol{\eta}}_{\tau_{k^{m}}}^{*}=\left(\hat{\boldsymbol{\eta}}_{\tau_{k} 1}^{*}, \hat{\boldsymbol{\eta}}_{\tau_{k}^{2}}, \cdots, \hat{\boldsymbol{\eta}}_{\tau_{k} M}^{*}\right)$。

6) 计算τ_k分位数下参数的样本协方差阵

$ \operatorname{Var}\left(\hat{\boldsymbol{\eta}}_{\tau_{k}}\right) \approx \frac{\sum\limits_{m=1}^{M}\left(\hat{\boldsymbol{\eta}}_{\tau_{k^{m}}}^{*}-\overline{\boldsymbol{\eta}}_{\tau_{k}}\right)\left(\hat{\boldsymbol{\eta}}_{\tau_{k^{m}}}^{*}-\overline{\boldsymbol{\eta}}_{\tau_{k}}\right)^{\mathrm{T}}}{M-1} $

式中，${\mathit{\boldsymbol{\overline \eta }} _{{\tau _k}}} = \frac{{\sum\limits_{m = 1}^M {\mathit{\boldsymbol{\widehat \eta }}_{{\tau _k}m}^*} }}{M}$为τ_k分位数下的样本均值。

2.2 均值漂移模型的影响分析 2.2.1 均值漂移模型

对(i₁, j₁)个观测值添加漂移项

$ \left\{\begin{array}{l} y_{i j}=\boldsymbol{x}_{ij}^{\mathrm{T}} \boldsymbol{\beta}+b_{i}+\varepsilon_{i j}, \text { 且 }(i, j) \neq\left(i_{1}, j_{1}\right) \\ y_{i_{1} j_{1}}=\boldsymbol{x}_{i_{1}j_{1}}^{\mathrm{T}} \boldsymbol{\beta}+b_{i_{1}}+\gamma_{i_{1}j_{1}}+\varepsilon_{i_{1}j_{1}}, \text { 当 }(i, j)=\left(i_{1}, j_{1}\right) \text { 时 } \end{array}\right. $

(10)

式中γ_i1j1是一个漂移项。记模型(10)的参数估计为${\mathit{\boldsymbol{\widehat \eta }}_{\{ {i_1}{j_1}\} }} = {\left({{{\mathit{\boldsymbol{\widehat \beta }}}_{\{ {i_1}{j_1}\} }}, {{\mathit{\boldsymbol{\widehat b}}}_{\{ {i_1}{j_1}\} }}, {{\hat \gamma }_{{i_1}{j_1}}}} \right)^{\rm{T}}}$。此时均值漂移模型在分位数τ_k(k=1, 2，…, q)下的加权损失函数为

$ \begin{array}{l} \ \ \ \ \ \ L_{\left\{i_{1} j_{1}\right\}}=\sum\limits_{k=1}^{q} \sum\limits_{i \neq i_{1}}^{n} \sum\limits_{j=1}^{n_{i}} w_{k} \rho_{\tau_{k}}\left(y_{i j}-b_{i}-\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}\left({\tau}_{k}\right)\right)+ \\ \sum\limits_{k=1}^{q} \sum\limits_{i=i_{1}} \sum\limits_{j \neq j_{1}}^{n_{i}} w_{k} \rho_{\tau_{k}}\left(y_{i_{1} j}-b_{i_{1}}-\boldsymbol{x}_{i_{1}j}^{\mathrm{T}} \boldsymbol{\beta}\left(\boldsymbol{\tau}_{k}\right)\right)+\lambda \sum\limits_{i=1}^{n}\left|b_{i}\right|+ \\ \sum\limits_{k=1}^{q} w_{h} \boldsymbol{\rho}_{\tau_{k}}\left(y_{i_{1} j_{1}}-b_{i_{1}}-\boldsymbol{x}_{i_{1} j_{1}}^{\mathrm{T}} \boldsymbol{\beta}\left({\tau}_{k}\right)-\gamma_{i_{1} j_{1} k}\right) \end{array} $

(11)

式中γ_i1j1k是分位数τ_k下的漂移项。均值漂移模型主要用来对每个数据点下的漂移项逐一进行假设检验：H_0k ∶γ_i1j1k=0或H_1k ∶γ_i1j1k≠0，其中k=1, 2，…, q。若拒绝H_0k，则说明在τ_k分位点下该数据点为异常值点。

2.2.2 γ_i1j1k的估计及数据删除模型和均值漂移模型系数估计的等价性

在分位数τ_k下，对式(11)关于γ_i1j1k进行极小化，可得

$ \rho_{\tau_{k}}\left(y_{i_{1} j_{1}}-\boldsymbol{x}_{i_{1} j_{1}}^{\mathrm{T}} \hat{\boldsymbol{\beta}}_{\left\{i_{1} j_{1}\right\}}\left(\tau_{k}\right)-\hat{b}_{\left\{i_{1} j_{1}\right\} i_{1} j_{1}}-\hat{\gamma}_{i_{1} j_{1} k}\right)=0 $

(12)

其中${\widehat {b}_{\{ {i_1}{j_1}\} {i_1}{j_1}}}$表示均值漂移模型中随机效应向量的估计值${{{\mathit{\boldsymbol{\widehat b}}}_{\{ {i_1}{j_1}\} }}}$的第i₁j₁个分量，由于ρ_τ(r)=0当且仅当r=0，因此可得

$ \hat{\gamma}_{i_{1} j_{1} k}=y_{i_{1} j_{1}}-\boldsymbol{x}_{i_{1} j_{1}}^{\mathrm{T}} \hat{\boldsymbol{\beta}}_{\left\{i_{1} j_{1}\right\}}\left(\tau_{k}\right)-\hat{b}_{\left\{i_{1} j_{1}\right\} i_{1} j_{1}} $

(13)

根据式(3)和式(11)可以看出数据删除模型和均值漂移模型的系数β的估计是等价的，由此可得

$ \hat{\gamma}_{i_{1} j_{1} k}=y_{i_{1} j_{1}}-\boldsymbol{x}_{i_{1} j_{1}}^{\mathrm{T}} \hat{\boldsymbol{\beta}}_{\left[i_{1} j_{1}\right]}\left(\tau_{k}\right)-\hat{b}_{\left[i_{1} j_{1}\right] i_{1} j_{1}} $

(14)

式中，${{{\mathit{\boldsymbol{\widehat \beta }}}_{\left[{{i_1}{j_1}} \right]}}}$(τ_k)和${\widehat {b}_{\left[{{i_1}{j_1}} \right]{i_1}{j_1}}}$是数据删除模型的参数估计。因此，可以利用式(14)构造出原假设H_0k的检验统计量。

2.2.3 诊断统计量

为了得到统计量的抽样分布，韦博成等^[13]在小样本中针对线性回归模型的异常值检验问题，采用方差分析的方法构造出检验统计量；曾林蕊等^[14]在误差的正态分布假设下，针对大样本的半参数广义线性模型，利用惩罚对数似然函数构建了Score检验统计量，给出了上述问题的拒绝域。本文在中小样本和非正态或非对称的模型误差假定下，构造了原假设H_0k下的Wald统计量

$ W=\left.\frac{\gamma \cdot \gamma}{\operatorname{Var}(\gamma)}\right|_{\gamma=\hat{\gamma}_{i_{1}j_{1} k}} $

(15)

式中，Var(γ)是漂移项的方差。统计量(15)在大样本下近似服从卡方分布，但是在中小样本下其分布难以确定。因此，本文采取Bootstrap法来构造上述统计量的拒绝域，过程可以分为两步：首先对统计量中的Var($\hat{\gamma}_{i_{1} j_{1} k}$)进行近似计算；其次利用统计量的Bootstrap样本构造假设检验的拒绝域。具体步骤如下所述。

1) 计算Var($\hat{\gamma}_{i_{1} j_{1} k}$)。与2.1.3节类似，首先利用原样本在τ=0.5下的参数估计生成残差集合{ε_ij}，然后在抽样中锁定残差集合的第(i₁, j₁)个样本不动，对其余的N－1个样本进行有放回地抽样，再合在一起生成容量为N的Bootstrap残差集合{${\widetilde \varepsilon _{ij}}$}，最后根据$\tilde{y}_{i j}=\boldsymbol{x}_{i j}^{\mathrm{T}} \hat{\boldsymbol{\beta}}\left({\tau}_{q / 2}\right)+\hat{b}_{i}+\widetilde{\varepsilon}_{i j}$生成Bootstrap样本(x, ${\mathit{\boldsymbol{\tilde y}}}$)_i1j1，其中β(τ_q/2)是分位数τ=0.5下的系数估计，并基于式(14)求解漂移项的估计，计算估计$\hat{\gamma}_{i_{1} j_{1} k}$的Bootstrap方差，记为Var($\tilde{\gamma}_{i_{1} j_{1} k}$)。

2)利用初始样本(x, y)求得$\hat{\gamma}_{i_{1} j_{1} k}$，结合步骤1)中的Var($\tilde{\gamma}_{i_{1} j_{1} k}$)，根据式(15)计算检验统计量^[15]，记为T₀。

3) 对初始样本在τ=0.5分位数下的误差项{ε_ij}进行M次有放回地抽样，生成Bootstrap误差项{ε_ij^*}，利用$y_{i j}^{*}=\boldsymbol{x}_{i j}^{\mathrm{T}} \hat{\boldsymbol{\beta}}\left(\tau_{q / 2}\right)+\hat{b}_{i}+\varepsilon_{i j}^{*}$获得Bootstrap样本(x, y^*)_i1j1，再将该样本漂移项的估计结果代入式(15)，得到检验统计量T^*_τkm, m=1, 2，…, M，k=1, 2, …, q。

4) 将分位数τ_k下的M个统计量从小到大重新排序，设定检验水平α，则T^*_τkm上的α分位点为第[M(1－α)]+1个，记为T^*_τkα，其中[A]表示对实数A向下取整。由此可以构造H_0k下的拒绝域为{T₀>T^*_τkα}。

3 数值模拟

在模拟中y_ij代表第i个个体的第j个观测值，根据如下模型生成数据。

$ y_{i j}=\boldsymbol{x}_{i j}^{\mathrm{T}} \boldsymbol{\beta}+b_{i}+\boldsymbol{\varepsilon}_{i j} $

(16)

假设$\boldsymbol{x}_{i j}=\left(1, \tilde{\boldsymbol{x}}_{i j}\right)^{\mathrm{T}}, \tilde{\boldsymbol{x}}_{i j}$服从标准正态分布N(0, 1)，随机效应b_i~N(0, 2)，参数β=(1, 2)^T，模型误差ε_ij~Exp(0.5)－2，其中Exp(λ)是参数为λ的指数分布，数学期望为$\frac{1}{\lambda }$。共20组数据，每组10个观测值。分位数取(0.1, 0.3, 0.5, 0.7, 0.9)。

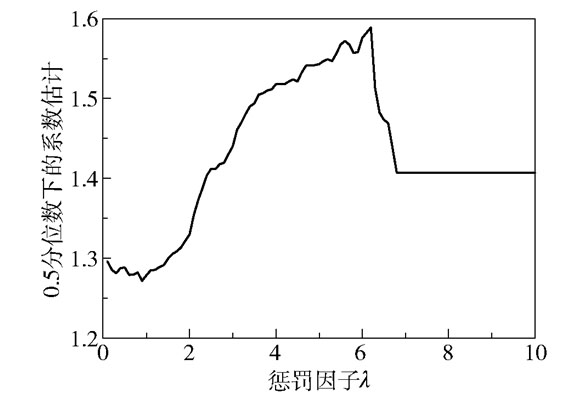
图 1是0.5分位数下模型的系数估计随惩罚因子λ的变化曲线，在λ大于7时系数不再发生变化，说明此时惩罚因子过大，导致随机效应不再起作用。针对线性混合模型(16)，利用R语言lme4包对其随机效应方差和误差方差进行估计，然后根据Koenker^[7]建议的方法，并结合图 1，在模拟中经过多次实验，最终选取λ=2。

为了验证本文提出的数据删除模型参数的一步近似估计的准确性，表 1给出了不同分位数下参数近似估计和直接计算的参数估计的对比情况，其中实验1~5分别为删去不同数据点所做的5次验证，评价指标设定为参数估计的相对偏差：bias(η)=$\frac{\left\|\hat{\boldsymbol{\eta}}_{0}-\hat{\boldsymbol{\eta}}_{1}\right\|_{1}}{\left\|\hat{\boldsymbol{\eta}}_{0}\right\|_{1}}$，其中${{{\mathit{\boldsymbol{\widehat \eta }}}_0}}$是采用R语言RQPD包直接逐一计算出的参数估计，作为真实估计，${{{\mathit{\boldsymbol{\widehat \eta }}}_1}}$是利用式(7)计算的CDM参数的近似估计结果，‖A‖₁表示向量A的一范数。可以看出CDM参数的近似估计结果与真实结果相接近，在样本量较大时，使用参数的近似估计可以减少计算时间。

3.1 针对单个点的影响分析

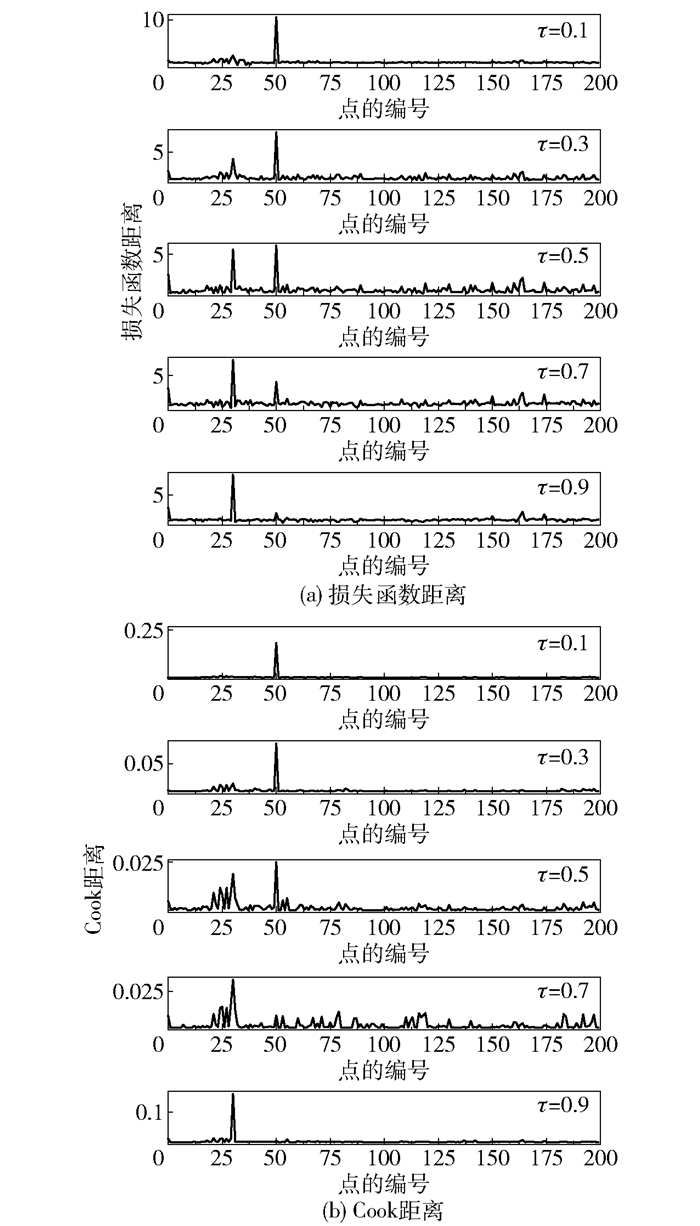
首先对单个数据中是否是强影响点或异常值点进行验证，实验可以分为两部分：针对单个数据是否为强影响点的诊断，和是否为异常值点的诊断。针对由模型(16)所生成的模拟数据，对第30个点和第50个点增加扰动，分别为y₃₀=y₃₀+6和y₅₀=y₅₀－6，然后采用本文提出的基于损失函数的距离和Cook距离来检测强影响点。强影响点检验结果如图 2所示。图 2(a)从上到下分别为分位数等于0.1、0.3、0.5、0.7、0.9时的损失函数距离。可以看出损失函数距离可以很好地检验出第30个和第50个点为强影响点，并且在不同分位数下不同位置的强影响点的表现不同：低分位数利于检验位于数据下方的强影响点，高分位数则对位于数据上方的强影响点敏感。图 2(b)是Cook距离的诊断结果，尽管结果的波动幅度与图 2(a)不同，但是结论相同，可以相互验证，避免出现方法不准确的问题。

基于相同的模拟数据，对其进行异常值点检验，结果展示在图 3中。图 3中虚线上方是Wald统计量的拒绝域，可以明显看出，图 3(a)中第30个和第50个点位于拒绝域，图 3(b)中第50个点是异常值点，同时结合图 2结果可知，异常值点与强影响点的检验结果相同，但是对比图 3(a)和(b)可以看出，低分位数下的结果对位于数据上方的异常值点更敏感。

3.2 针对同一个体一组点的影响分析

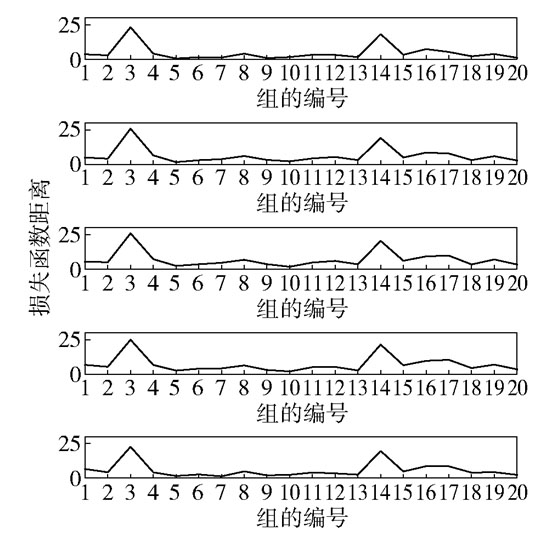
对属于同一个体的一组数据是否为强影响点或异常值点的情形进行检验，类似于3.1节实验，分为针对强影响点的诊断和针对异常值点的诊断。对初始模拟数据的第3组数据和第14组数据进行扰动：y_3·=y_3·+6和y_14·=y_14·－6。篇幅所限，图 4仅展示一组强影响点的损失函数距离的检验结果。从图 4可以看出第3组和第14组数据的损失函数距离明显大于其他组，因此为强影响点，说明即使是在同一个体的一组数据都是强影响点的情况下，本文所提方法也具有良好的检验能力。

4 实验验证与分析

实验数据共包含216个观测值，其中辐解剂量有1、2、4、6、8、10(10³ Gy)共6个水平，硝酸浓度也有0.2、0.4、0.6、0.8、1.0、1.5 mol/L共6个水平，HSC浓度为0.1、0.2、0.4、0.6、0.8、1.0 mol/L共6个水平。根据1.1节数据描述的结果，以辐解剂量作为解释变量X_ij，硝酸浓度和HSC浓度的联合影响作为随机效应μ_i，共有36个取值。响应变量c_ij表示为不同实验条件下生成的铵根离子浓度(mmol/L)。为了对响应变量进行影响因素分析，可建立如下线性混合效应模型

$ c_{i j}=\beta_{0}+\beta_{1} \boldsymbol{X}_{i j}+\mu_{i}+\varepsilon_{i j} $

(17)

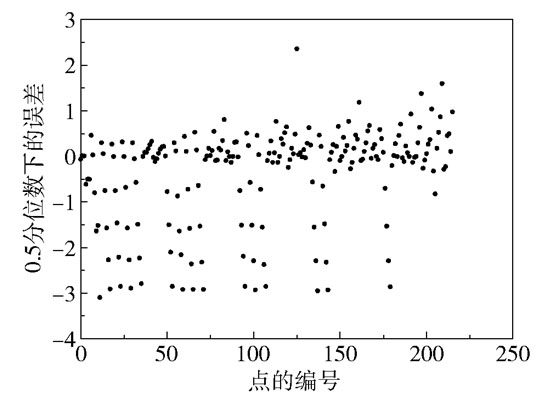
式中，i=1, …, 36，j=1, …, 6。基于模型(17)在0.5分位数下的参数估计作误差散点图，如图 5所示，可以看出误差在零点上下波动，但是在上侧波动小而密集，在下侧波动大而疏松，可以明显得出数据总体上既不是对称分布，也不是正态分布，因此选择采用本文方法对其进行影响分析。

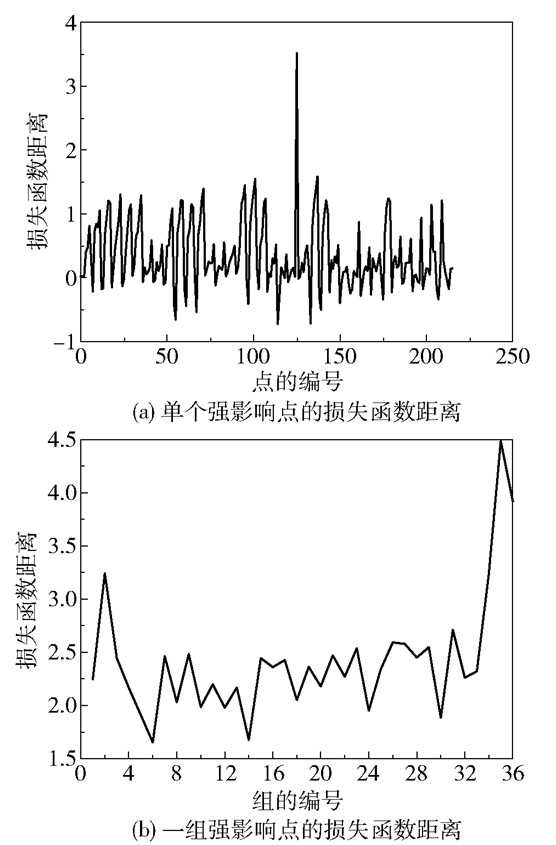
由于在低分位数下检验结果不存在明显的强影响点，所以图 6仅展示了τ=0.9时的检验结果。从图 6可以看出，在0.9的分位数下，第125个数据点和第35组数据相较于其他数据明显突出，结合图 5可知二者均是位于数据上方的强影响点。

5 结束语

本文针对服从非对称、非正态，尤其是重尾或轻尾分布的纵向数据的影响分析问题，在中等样本下利用线性混合模型的分位数估计，分别构建检测强影响点的基于损失函数的距离和Cook距离，以及识别异常值点的Wald统计量。此外，为了减少计算量，给出数据删除模型参数的一步近似估计，并且利用Bootstrap方法求得统计量的拒绝域。模拟结果表明，本文所提的诊断度量和诊断统计量都可以很好地检验出数据中的强影响点和异常值点，实证分析结果也进一步证明了本文方法的实用性。