2. 常熟理工学院 材料工程学院, 常熟 215500
2. School of Materials Engineering, Changshu Institute of Technology, Changshu 215500, China
硝酸胍(GN)是一种新型的精细化工产品,外观多为白色结晶粉末或颗粒,是医药、农药、染料、炸药等化工原料的重要中间体[1],同时也是汽车安全气囊的新型气体发生剂,其广泛应用于医药合成、消毒剂、油漆工业、火箭推进剂等众多领域。
硝酸胍因具有强氧化性,被认定属于危险品5.1范畴[2],遇明火、摩擦、碰撞、打击等可发生爆炸,高温下易发生分解、燃烧和爆炸,生成有毒的氮氧化物等物质。硝酸胍的分子式为CH6N4O3,含有硝基活性基团,性质极不稳定,可以在不需要外界氧的参与下自发分解[3],增大了其在生产、储运和使用过程中的危险性。例如2012年2月28日,河北克尔化工有限公司发生的重大火灾爆炸事故[4],就是由于硝酸胍和未反应完的硝酸铵局部受热,二者急剧分解发生爆炸,又引爆堆放在反应釜附近的硝酸胍,发生二次爆炸,事故造成25人死亡、4人失踪、46人受伤,爆炸所释放的能量相当于6.05吨三硝基甲苯(TNT)。因此,研究硝酸胍的热解行为具有重要的实际意义。Sankaranarayanan等[5]通过热重-红外-质谱联用(T G- F T- I R- MS)分析硝酸胍的热分解行为,指出其主要分解产物为NH3、N2O、NO2、H2O和CO2。王学志[3]通过差示扫描量热法(DSC)测定硝酸胍的热流曲线,结果表明硝酸胍的分解存在吸放热耦合现象,符合自催化反应特征。王凯[6]指出对于存在耦合现象的物质,通过热重数据进行热动力学计算,能在一定程度上避免或减弱熔融吸热和分解放热之间的影响。硝酸胍具有较大的热危险性,但目前对其热动力学分析的研究较少,对热安全应用参数的研究尚未展开。因此,本文采用热重分析法,通过不同的线性升温速率来探究硝酸胍的热分解过程,利用Flyn n- Wal l- Ozawa(FWO)和Kissinger Akahira and Sunose(KAS)法估算其表观活化能,采用Coat s- Redfern(CR)法探究最适反应机理函数,并计算其热安全性参数,研究结果可以为硝酸胍的生产、储运及使用过程中的安全应用提供理论参考。
1 实验部分 1.1 实验原料硝酸胍,分析纯,阿拉丁试剂(上海)有限公司。
1.2 实验方法采用STA449F5型同步热分析仪(德国NETZSCH仪器制造有限公司)进行热重法分析。取约7 mg硝酸胍于氧化铝坩埚中进行热分析测试,温度范围为450~700 K,升温速率为5、10、15、20 K/min,吹扫气和保护气均为氮气,气体流量为50 mL/min。
采用DSC 250型差示扫描量热仪(美国TA仪器公司)进行DSC信号测试。由于蓝宝石是单晶氧化铝(α-Al2O3),其物化性质稳定,可提高比热容实验的准确性,故采用蓝宝石法测定比热容,并在开始和结束段各设5 min的等温段,以补偿温度漂移,即303.15 K时恒温5 min,然后以10 K/min的升温速率升至373.15 K,再恒温5 min。
上述实验均在相对密闭的空间中进行,以减小热量损失。
2 结果与讨论 2.1 硝酸胍热分解过程图 1为硝酸胍在5、10、15、20 K/min的升温速率下的TG和微商热重(DTG)曲线,表 1为硝酸胍的热分解参数。由结果可知,硝酸胍在450~700 K的温度范围内呈一步失重,TG的平均外推起始温度为580.28 K,平均外推终止温度为607.78 K,该阶段为硝酸胍的主要分解阶段,反应速率较大,700 K时平均质量残留率为18.74%。不同升温速率并未改变硝酸胍的热分解过程,但随着升温速率的增大,硝酸胍的分解过程存在滞后效应,即分解的外推起始温度、峰值温度和外推终止温度均向高温方向推移,且最大热解速率增大。
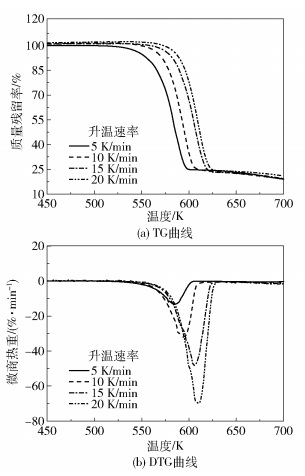
|
图 1 不同升温速率下硝酸胍的热分解曲线 Fig.1 Thermal decomposition curves of guanidine nitrate at different heating rates |
| 下载CSV 表 1 硝酸胍的热分解参数 Table 1 Thermal decomposition parameters of guanidine nitrate |
根据热动力学理论,在非等温非均相体系中,动力学方程可表示为[7]
| $ \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \left( {\frac{1}{\beta }} \right)k\left( T \right)f\left( \alpha \right) $ | (1) |
式中,α为转化率;T为热力学温度,K;β为升温速率,K/min;k(T)为反应速率常数;f(α)为微分机理函数。其中,转化率α可表示为[7]
| $ \alpha = \frac{{{m_0} - {m_t}}}{{{m_t} - {m_\infty }}} $ | (2) |
式中,m0为起始质量,g;mt为任意时刻t的质量,g;m∞为最终质量,g。
根据Arrhenius方程,反应速率常数k(T)和热力学温度T的关系可表示为[7]
| $ k\left( T \right) = A{\rm{exp}}\left( { - \frac{{{E_\alpha }}}{{RT}}} \right) $ | (3) |
式中,A为指前因子;Eα为表观活化能,kJ/mol;R为摩尔气体常数,8.314 J/(mol ·K)。
联立式(1)和(3),热动力学方程可写为
| $ \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \left( {\frac{A}{\beta }} \right){\rm{exp}}\left( { - \frac{{{E_\alpha }}}{{RT}}} \right)f\left( \alpha \right) $ | (4) |
其中,积分和微分的关系式可表示为[7]
| $ g\left( \alpha \right) = \int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_{{T_0}}^T {{\rm{esp}}\left( { - \frac{{{E_\alpha }}}{{RT}}} \right)} {\rm{d}}T $ | (5) |
式中,g(α)为积分机理函数。
2.2.1 无模型拟合法无模型拟合法,又称等转化率法,是指在不假定反应机理函数的情况下直接求取表观活化能Eα的方法,避免了因假设不同的反应机理而导致的误差[8-9],其广泛应用于热动力学分析。常用的无模型拟合法有FWO法、KAS法和Friedman法等。
本文对450~700 K的温度范围内硝酸胍的分解过程进行热动力学分析,采用FWO法和KAS法对转化率在0.1~0.9内的曲线数据进行线性拟合。
FWO法中,热动力学方程可表示为[7]
| $ {\rm{lg}}\beta = {\rm{lg}}\frac{{A{E_\alpha }}}{{Rg\left( \alpha \right)}} - 2.315 - 0.4567\frac{{{E_\alpha }}}{{RT}} $ | (6) |
KAS法中,热动力学方程可表示为[7]
| $ {\rm{ln}}\left( {\frac{\beta }{{{T^2}}}} \right) = {\rm{ln}}\frac{{A{E_\alpha }}}{{Rg\left( \alpha \right)}} - \frac{{{E_\alpha }}}{{RT}} $ | (7) |
图 2和图 3分别为不同转化率下FWO和KAS法的拟合曲线,拟合参数(Eα和相关系数r)见表 2。从表 2可以看出,FWO和KAS法得到的r值均较高,说明线性拟合较好。FWO法得到的表观活化能范围为110.80~155.65 kJ/mol,平均值为140.43 kJ/mol;KAS法得到的表观活化能范围为107.01~153.57 kJ/mol,平均值为137.82 kJ/mol。两种方法得到的表观活化能相差较小,且表观活化能都具有随转化率的升高而增大的趋势,说明反应难度随反应程度的加大而增加。

|
图 2 不同转化率下FWO法的拟合曲线 Fig.2 Fitting curves of the FWO method for different conversion rates |
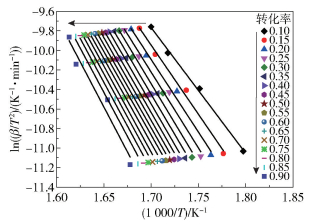
|
图 3 不同转化率下KAS法的拟合曲线 Fig.3 Fitting curves of the KAS method for different conversion rates |
| 下载CSV 表 2 不同转化率α下FWO和KAS法的拟合参数 Table 2 Fitting parameters of FWO and KAS methods for different conversion rates |
由FWO和KAS法求得的表观活化能均小于180 kJ/mol,根据固体物质活化能指标自燃倾向性分级标准[10-11],硝酸胍的自燃倾向等级为Ⅰ级,自燃倾向性大,热危险性大。
图 4为FWO和KAS法中转化率α与表观活化能Eα的关系曲线。由图中可以看出,FWO和KAS法中转化率与表观活化能的拟合曲线近似平行,规律呈现一致性。FWO和KAS法曲线拟合的关系式可分别表示为式(8)和式(9),决定系数(R2)均为0.993。
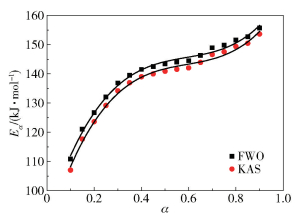
|
图 4 FWO和KAS法中转化率与表观活化能的关系曲线 Fig.4 Relation between conversion rate and apparent activation energy in the FWO and KAS methods |
| $ {E_\alpha } = 90.68 + 250.68\alpha - 400.33{\alpha ^2} + 225.63{\alpha ^3} $ | (8) |
| $ {E_\alpha } = 86.03 + 261.45\alpha - 418.05{\alpha ^2} + 235.59{\alpha ^3} $ | (9) |
模型拟合法涉及反应机理函数,因此可同时求算活化能与指前因子[12]。本文选取20 K/min升温速率下的热分解曲线,采用CR法进行拟合,其热动力学方程可表示为[7]
| $ {\rm{ln}}\left( {\frac{{g\left( \alpha \right)}}{{{T^2}}}} \right) = \ln \frac{{AR}}{{\beta {E_\alpha }}} - \frac{{{E_\alpha }}}{{RT}} $ | (10) |
表 3为常见的13种固体热解反应机理[7],通过CR法求得其表观活化能,探究硝酸胍的最适机理函数,拟合曲线见图 5,计算结果见表 4。由表 4可以看出,由Avram i- Erofeev(A2)得出的表观活化能为140.55 kJ/mol,最接近由FWO和KAS法计算的平均表观活化能140.43 kJ/mol和137.82 kJ/mol,表明Avram i- Erofeev(A2),即二维随机成核及增长模型最能反映硝酸胍的分解机理,其反应机理函数可表示为
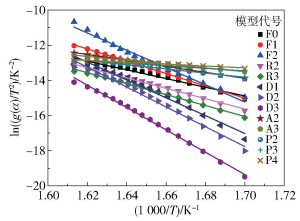
|
图 5 CR法中反应机理函数拟合曲线 Fig.5 Fitting curves of the reaction mechanism function by the CR method |
| 下载CSV 表 4 CR法估算表观活化能 Table 4 Apparent activation energies obtained using the CR method |
| $ \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \frac{{9.58 \times {{10}^8}}}{\beta }{{\rm{e}}^{\frac{{ - 1.41 \times {{10}^5}}}{{RT}}}} \times 2\left( {1 - \alpha } \right){\left[ { - {\rm{ln}}\left( {1 - \alpha } \right)} \right]^{\frac{1}{2}}} $ | (11) |
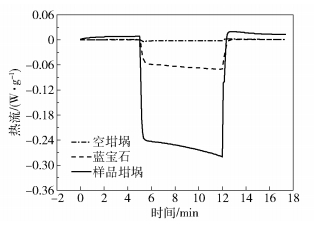
采用蓝宝石法,以等温-动态-等温的模式,分别对空坩埚、蓝宝石和样品坩埚进行DSC信号测试,结果见图 6。通过公式(12)得到不同温度下硝酸胍的比热容[13],结果如表 5所示。
|
图 6 空坩埚、蓝宝石和样品坩埚的DSC信号曲线 Fig.6 DSC signal curves of the empty crucible, sapphire and sample crucible |
| 下载CSV 表 5 不同温度下硝酸胍的比热容 Table 5 Specific heat capacities of guanidine nitrate at different temperatures |
| $ {c_p} = \frac{{\left( {{\mathit{\Phi }_{{\rm{meas}}}} - {\mathit{\Phi }_{{\rm{sap}}}}} \right){m_{{\rm{sap}}}}}}{{\left( {{\mathit{\Phi }_{{\rm{sap}}}} - {\mathit{\Phi }_{{\rm{bl}}}}} \right){{\rm{m}}_{{\rm{eas}}}}}}{c_{p\left( {{\rm{sap}}} \right)}} $ | (12) |
式中,cp为样品的比热容,J/(g ·K);Φmeas为样品的DSC信号,mW;Φsap为蓝宝石的DSC信号,mW;Φbl为空坩埚的DSC信号,mW;msap为蓝宝石的质量,g;mmeas为样品的质量,g;cp(sap)为蓝宝石的比热容,J/(g ·K)。
由表 5可知,在310~370 K的温度范围内,硝酸胍的比热容随温度的升高而逐渐增大,平均值为3.148 J/(g ·K)。
2.3.2 自加速分解温度自发火温度(Tbe0)是指物质自加热着火的最低环境温度,是物质热安全性的参数之一。自加速分解温度(TSADT)是指反应性化学物质在7日内发生自加速分解的最低环境温度[14],是评价物质热危险性的重要指标。
根据GJB 772A—1997[15],由不同升温速率下DTG的外推起始温度Te,按式(13)进行线性回归计算,可得升温速率β趋于0时的外推起始温度(Te0),由Te0=TSADT,可得硝酸胍的自加速分解温度[16-17]。由热力学关系式(14),代入Te0,可得到Tbe0。
| $ {T_{{\rm{e}}i}} = {T_{{\rm{e0}}}} + b{\beta _i} + c\beta _i^2 + d\beta _i^3, i = 1, 2, 3, 4 $ | (13) |
| $ {T_{{\rm{be0}}}} = \frac{{{E_\alpha } - \sqrt {E_\alpha ^2 - 4{E_\alpha }R{T_{{\rm{e0}}}}} }}{{2R}} $ | (14) |
式中,Tei为升温速率βi时的外推起始温度,K;b、c、d为方程的系数;Eα取FWO和KAS法的平均值[18-19]。
经计算,硝酸胍的自加速分解温度为530.15 K,自发火温度为548.10 K。通过实验研究和理论计算可知,硝酸胍在生产、储运及使用过程中,应严格控制周围环境温度,不得高于530.15 K,以避免热量累积及热失控事件的发生。
2.3.3 活化参数活化熵(ΔS≠)、活化焓(ΔH≠)和活化自由能(ΔG≠)是评价物质热安全性的重要参数,其中,ΔS≠表示体系的混乱程度,熵值越小,体系越有序;ΔH≠表示反应的总能耗,焓值越小,越有利于形成活化络合物;ΔG≠表示形成活化络合物系统的总能量的增加量[20-21]。根据过渡态理论,结合公式(15)~(17),分别计算Te和Tp下的活化参数,结果见表 6。
| $ k\left( T \right) = A{\rm{exp}}\left( { - \frac{{{E_\alpha }}}{{RT}}} \right) = {K_{\rm{B}}}\frac{T}{h}{\rm{exp}}\left( { - \frac{{\Delta {G^ \ne }}}{{RT}}} \right) $ | (15) |
| $ \Delta {H^ \ne } = {E_\alpha } - RT $ | (16) |
| $ \Delta {G^ \ne } = \Delta {H^ \ne } - T\Delta {S^ \ne } $ | (17) |
式中,KB为玻耳兹曼常量,1.380 7×10-23 J/K;h为普朗克常数,6.626×10-34 J/s。
由表 6可知,ΔS≠和ΔH≠随升温速率的增大而减小,表明升温速率增大,体系的有序性增加,且有利于活化络合物的形成;ΔG≠和k(T)随升温速率的增大而增大,其中,ΔG≠正值较高,表明活化络合物很不稳定,在外界作用下易向正反应方向进行[22-23],k(T)的增加,表明反应速率加快,这与图 1的DTG曲线趋势相一致。
| 下载CSV 表 6 硝酸胍的活化参数 Table 6 Activation parameters of guanidine nitrate |
(1) 硝酸胍在5、10、15、20 K/min的升温速率下,在450~700 K的温度范围内呈一步失重,热重法的平均外推起始温度为580.28 K,700 K时平均质量残留率为18.74%。不同升温速率并未改变硝酸胍的热分解过程,但随着升温速率的增大,硝酸胍的分解存在滞后效应。
(2) 采用FWO和KAS法对转化率在0.1~0.9内的曲线数据进行线性拟合,得到表观活化能的平均值分别为140.43 kJ/mol和137.82 kJ/mol,自燃倾向等级为Ⅰ级。表观活化能随转化率的升高而增大,说明反应难度随反应程度的加大而增加。通过CR法可知,Avram i- Erofeev(A2)模型最能反映硝酸胍的分解机理。
(3) 在310~370 K的温度范围内,硝酸胍的比热容随温度的升高而逐渐增大,比热容的平均值为3.148 J/(g ·K)。自加速分解温度(TSADT)和自发火温度(Tbe0)分别为530.15 K和548.10 K。活化熵和活化焓随升温速率的增大而减小,活化自由能和反应速率常数随升温速率的增大而增大。
| [1] |
柏薇薇, 姚旭明, 苏建国. 硝酸胍生产方法与用途[J]. 辽宁化工, 2012, 41(12): 1240-1241. BAI W W, YAO X M, SU J G. Production and application of guanidine nitrate[J]. Liaoning Chemical Industry, 2012, 41(12): 1240-1241. (in Chinese) DOI:10.3969/j.issn.1004-0935.2012.12.004 |
| [2] |
中华人民共和国国家技术监督局.常用危险化学品的分类及标志: GB 13690—1992[S].北京: 中国标准出版社, 1992. The State Bureau of Quality and Technical Supervision of the People's Republic of China. Classification and labeling of commonly used hazardous chemicals: GB 13690—1992[S]. Beijing: Standards Press of China, 1992. (in Chinese) |
| [3] |
王学志.硝酸胍热失控机理研究[D].青岛: 中国石油大学(华东), 2017. WANG X Z. Study on thermal runaway mechanism of guanidine nitrate[D]. Qingdao: China University of Petroleum (East China), 2017. (in Chinese) |
| [4] |
赵丹. 河北克尔化工"2·28"特大爆炸事故[J]. 现代班组, 2015(8): 24-25. ZHAO D. "2·28" extraordinary explosion accident in Hebei Kerr chemical Co., Ltd[J]. Xian Dai Ban Zu, 2015(5): 24-25. (in Chinese) |
| [5] |
SANKARANARAYANAN A, MALLICK L, KUMBHAKARNA N R. A numerical and experimental study of the decomposition pathways of guanidinium nitrate[J]. Journal of Thermal Analysis and Calorimetry, 2018, 131: 427-441. DOI:10.1007/s10973-017-6707-4 |
| [6] |
王凯.含能材料自催化分解特性与热安全性研究[D].南京: 南京理工大学, 2016. WANG K. Research on the thermal autocatalytic decomposition characteristics and thermal safety of energetic materials[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese) |
| [7] |
胡荣祖, 史启祯. 热分析动力学[M]. 2版.. 北京: 科学出版社, 2008. HU R Z, SHI Q Z. Thermal analysis kinetics[M]. 2nd ed.. Beijing: Science Press, 2008. (in Chinese) |
| [8] |
MAMLEEV V, BOURBIGOT S, LE BRAS M, et al. Model-free method for evaluation of activation energies in modulated thermogravimetry and analysis of cellulose decomposition[J]. Chemical Engineering Science, 2006, 61(4): 1276-1292. DOI:10.1016/j.ces.2005.07.040 |
| [9] |
JORAID A A, ALAMRI S N, ABU-SEHLY A A. Model-free method for analysis of non-isothermal kinetics of a bulk sample of selenium[J]. Journal of Non-Crystalline Solids, 2008, 354(28): 3380-3387. DOI:10.1016/j.jnoncrysol.2008.02.002 |
| [10] |
阳富强, 吴超. 硫化矿自燃预测预报理论与技术[M]. 北京: 冶金工业出版社, 2011. YANG F Q, WU C. Prediction and forecast of spontaneous combustion of sulfide minerals-theory and technology[M]. Beijing: Metallurgical Industry Press, 2011. (in Chinese) |
| [11] |
张淑娟, 江美丽, 彭孟春, 等. 连二亚硫酸钠热分解特性动力学及危险性评价[J]. 安全与环境学报, 2014, 14(5): 39-44. ZHANG S J, JIANG M L, PENG M C, et al. Thermal decomposition kinetics behavior and the hazard assessment of sodium dithionite[J]. Journal of Safety and Environment, 2014, 14(5): 39-44. (in Chinese) |
| [12] |
孙琦.不同加热条件下硝酸铵的热危险性及氧化铜的影响[D].合肥: 中国科学技术大学, 2019. SUN Q. Thermal hazards of ammonium nitrate and effect of copper oxide under different heating experiments[D]. Hefei: University of Science and Technology of China, 2019. (in Chinese) |
| [13] |
俞进阳.烟花爆竹用烟火药剂的热危险性研究[D].南京: 南京理工大学, 2013. YU J Y. Research on the thermal hazard of the pyrotechnics for fireworks and crakers[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese) |
| [14] |
United Nations Organization. Recommendations on the transport of dangerous goods: model regulations[M]. New York: United Nations, 2010.
|
| [15] |
国防科学技术工业委员会.炸药试验方法: GJB 772A—1997[S].北京: 国防科工委军标出版社, 1997. Commission of Science, Technology and Industry for National Defense. Explosive test method: GJB 772A—1997[S]. Beijing: Military Standard Press of Commission of Science, Technology and Industry for National Defense, 1997. (in Chinese) |
| [16] |
仪建华, 徐司雨, 马晓东, 等. 太根发射药的非等温热分解反应动力学[J]. 火炸药学报, 2007, 30(4): 76-80. YI J H, XU S Y, MA X D, et al. Non-isothermal thermal decomposition reaction kinetics of TEGDN gun propellant[J]. Chinese Journal of Explosives & Propellants, 2007, 30(4): 76-80. (in Chinese) |
| [17] |
杜旭杰, 李晓东, 邹美帅, 等. 含能三唑硝酸盐的热动力学行为及其热抵抗力[J]. 北京理工大学学报, 2015, 35(12): 1315-1320. DU X J, LI X D, ZOU M S, et al. Thermokinetic behavior and heat-resistance stabilities of energetic triazole nitrates[J]. Transactions of Beijing Institute of Technology, 2015, 35(12): 1315-1320. (in Chinese) |
| [18] |
方将来, 齐敏, 华敏, 等. 杂质对过氧化苯甲酰的热分解危险性研究[J]. 化学工程, 2017, 45(9): 58-61, 78. FANG J L, QI M, HUA M, et al. Risk of impurities on thermal decomposition of benzoyl peroxide[J]. Chemical Engineering, 2017, 45(9): 58-61, 78. (in Chinese) |
| [19] |
高杰, 罗一鸣, 王浩, 等. 杂质对DNTF的热分解危险性研究[J]. 火工品, 2019(3): 47-50. GAO J, LUO Y M, WANG H, et al. Risk of impurities on thermal decomposition of DNTF[J]. Initiators & Pyrotechnics, 2019(3): 47-50. (in Chinese) |
| [20] |
HE Y Y, CHANG C, LI P, et al. Thermal decomposition and kinetics of coal and fermented cornstalk using thermogravimetric analysis[J]. Bioresource Technology, 2018, 259: 294-303. DOI:10.1016/j.biortech.2018.03.043 |
| [21] |
张天民. 可逆反应的自发性能用ΔG判断吗[J]. 化学教育, 2017, 38(9): 63-65. ZHANG T M. Whether the spontaneity of reversible reaction can be judged by its Gibbs free energy change[J]. Chinese Journal of Chemical Education, 2017, 38(9): 63-65. (in Chinese) |
| [22] |
ACEMIOGLU B, ALMA M H. Kinetics of wood phenolysis in the presence of HCl as catalyst[J]. Journal of Applied Polymer Science, 2002, 85(5): 1098-1103. |
| [23] |
周宇, 韩望, 袁大伟, 等. 沙柳材液化的反应动力学研究[J]. 山东农业大学学报(自然科学版), 2017, 48(1): 36-40. ZHOU Y, HAN W, YUAN D W, et al. Study on the liquefaction kinetics of Salix psammophila[J]. Journal of Shandong Agricultural University (Natural Science), 2017, 48(1): 36-40. (in Chinese) |








