2. 北京化工大学 机电工程学院, 北京 100029;
3. 中国航发湖南动力机械研究所 中国航空发动机集团航空发动机振动技术重点实验室, 株洲 412002
2. College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029;
3. AECC Key Laboratory of Aero-engine Vibration Technology, AECC Hunan Aviation Powerplant Research Institute, Zhuzhou 412002, China
滚动轴承是机械设备中最常用,同时也是最易损坏的重要零部件之一,因其工作环境相对复杂,内圈、外圈、滚动体等任意一个部分发生损伤,都将会给设备的正常运行埋下安全隐患[1]。因此,滚动轴承的状态监测和故障诊断受到了广泛的关注。轴承发生故障冲击时,故障信号大多数表现为非平稳的脉冲信号,宽度较窄。随着设备复杂性的提高,在利用振动传感器采集振动信号时,常常会包含轴承之外的其他振源信号,在实际测量中,设备的工频以及其他振源信号往往会淹没故障冲击信号,对滚动轴承的故障诊断造成阻碍。因此,有必要在后续轴承故障诊断之前进行信号降噪[2]。
针对上述问题,已有许多学者作出了探索。Ha等[3]提出了一种基于自相关的时间同步平均方法,可作为行星齿轮箱故障诊断的一种改进的预处理技术。张丹等[4]将经验模态分解(EMD)和线性预测滤波相结合,结果表明该方法能准确地检测滚动轴承故障。张盈盈等[5]采用自适应噪声消除(ANC)技术作为信号预处理的工具,去掉轴承振动信号中的工频及谐波。张西宁等[6]提出一种局部倒频谱方法,可以成功提取复杂振动信号中的干扰成分,抑制其对微弱故障诊断的干扰。朱敏等[7]结合完整集成经验模态分解(CEEMDAN)与自适应滤波中的最小均方算法(LMS)有效实现了轴承信号的降噪。杨晓雨等[8]提出一种LMS算法降噪、Fast-Kurtogram选频和共振解调技术相结合的滚动轴承故障诊断方法,并验证了该方法在滚动轴承早期故障诊断中的适用性。
除了以LMS为代表的ANC算法,其余各算法均是利用噪源信号的周期性对其进行去除。在工程实际中,由于载荷波动、机械启动停止等因素影响,轴承的运行往往处于变转速状态[9],导致上述利用周期性进行去噪的算法失效,而且变转速工况复杂,比匀转速工况更容易引发故障。虽然变转速过程更能凸显故障特征,但其干扰和背景噪声更强,微弱故障特征更难提取。针对变转速下的降噪问题,Borghesani等[10]将循环平稳分析方法与阶次跟踪技术相结合以弥补变转速运行模式带来的干扰。而在角域中去除噪声及多次重采样、逆采样也必将影响混合信号中的轴承故障成分。然而阶次跟踪在重采样时间计算和重采样幅度估计上均存在误差,包络信号的变形会引起脉冲峰值的角度间隔发生变化,从而直接影响包络分析结果的准确性[11]。而对于ANC算法,虽然不受周期性限制,但其必须依靠在特定位置加装的振动传感器才能获取理想的参考信号。附加传感器位置将决定整个算法的效果,理论上要求传感器拾取得到的参考信号只与噪声或故障源相关,而实际上满足这一要求的附加传感器位置并不是在每个设备上都存在。因此,如何在变转速的工作模式下,不依赖辅助设备且尽量不影响目标轴承信号来进行去噪是当前研究面临的主要问题。
通过分数阶傅里叶变换(FrFT),信号在适当的分数阶傅里叶域内可产生最佳能量聚集性,基于此,本文提出了一种基于FrFT滤波和LMS的故障诊断方法。由于故障一倍频能量往往最高,通过峰值搜索FrFT找出故障一倍频对应的最佳阶次和分数阶域聚集位置,据此进行FrFT滤波,得到的滤波信号作为LMS算法中仅与故障源相关的参考信号再进行自适应滤波。该方法不需要额外添设参考传感器,且降噪过程不影响目标轴承信号,成功实现了在强噪声背景下变转速轴承的微弱故障诊断。
1 LMS和FrFT基础理论 1.1 最小均方算法LMS是一种自适应滤波算法,即当输入信号的统计特性未知或随时间变化时,可通过自适应算法改变滤波器的权值向量,以达到最佳滤波效果。LMS可以描述成一个由滤波环节和自适应环节组成的反馈环,并以均方差最小为滤波准则。其中,滤波环节通过构造横向滤波器计算输入信号的响应并得到相应的估计误差,而自适应环节则以估计误差为基础,利用算法对横向滤波器的权值向量进行自适调节以实现自适应滤波。LMS算法性能稳定、结构简单且易于实现,因而应用广泛,其基本原理是将被噪声污染的信号与参考信号进行抵消运算,从而消除信号中的噪声[12],滤波效果重点在于参数信号仅需要与噪声信号或轴承故障信号相关。
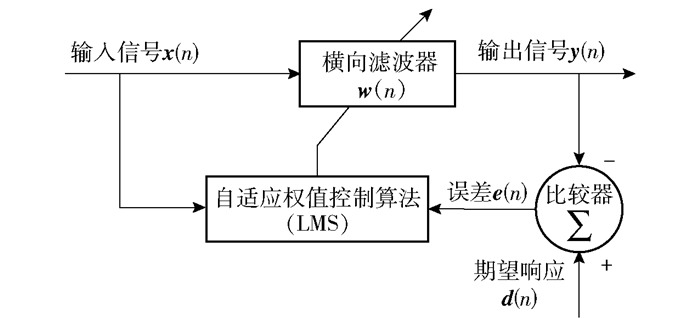
LMS结构分为横向滤波器、比较器和自适应权值控制算法,其算法框图如图 1所示。其中,x(n)为输入信号,d(n)为期望响应,w(n)为横向滤波器权值向量,y(n)为横向滤波器的输出信号,是对目标信号的估计值,可由输入信号向量与相应的权值矩阵乘积得到,e(n)为期望响应d(n)与滤波器输出之间的估计误差。LMS对应的算法如下。
| $ {\mathit{\boldsymbol{y}}(n) = {\mathit{\boldsymbol{w}}^{\rm{T}}}(n)\mathit{\boldsymbol{x}}(n)} $ | (1) |
| $ {\mathit{\boldsymbol{e}}(n) = \mathit{\boldsymbol{d}}(n) - \mathit{\boldsymbol{y}}(n)} $ | (2) |
| $ {\mathit{\boldsymbol{w}}(n + 1) = \mathit{\boldsymbol{w}}(n) + \mu \mathit{\boldsymbol{x}}(n)\mathit{\boldsymbol{e}}(n)} $ | (3) |
|
图 1 LMS算法框图 Fig.1 Schematic illustration of the LMS algorithm |
式中μ为步长因子,用于控制滤波器的收敛速度和稳定性。为了使系统稳定,步长因子的范围为0 < μ < 1/λmax,λmax为输入信号自相关矩阵的最大特征值。
一般地,自适应滤波算法会通过不断地调节权值向量以逼近维纳滤波最优解,而基于LMS的自适应滤波算法则是使滤波器输出信号与期望输出信号之间的估计误差的均方值最小,以达到对有用信号的最佳估计,其中估计误差的均方值如式(4)所示。
| $ E\left[ {{\mathit{\boldsymbol{e}}^2}(n)} \right] = E\left( {{{\left[ {\mathit{\boldsymbol{d}}(n) - {\mathit{\boldsymbol{w}}^{\rm{T}}}(n)\mathit{\boldsymbol{x}}(n)} \right]}^2}} \right) $ | (4) |
函数x(n)的p阶分数阶傅里叶变换可表示为Xp(u)或Fp[x(t)](u),其中Fp表示作用在x(n)上的算子[13-14],其基本定义为
| $ {\mathit{\boldsymbol{X}}_p}(u) = {{\rm{F}}^p}[\mathit{\boldsymbol{x}}(t)](u) = \int_{ - \infty }^{ + \infty } \mathit{\boldsymbol{x}} (t){K_p}(u, t){\rm{d}}t $ | (5) |
式中,FrFT的核函数Kp(u, t)计算如下。
| $ \begin{array}{l} {K_p}(u,t) = \\ \left\{ {\begin{array}{*{20}{l}} {{A_\alpha }{{\rm{e}}^{{\rm{j\pi }}\left( {{t^2}\cot \alpha + {u^2}\cot \alpha - 2tucsc\alpha } \right)}},}&{\alpha \ne n{\rm{\pi }}}\\ {{\rm{\delta }}(u - t),}&{\alpha = 2n{\rm{\pi }}}\\ {{\rm{\delta }}(u + t),}&{\alpha = (2n \pm 1){\rm{\pi }}} \end{array}} \right. \end{array} $ | (6) |
其中,p是FrFT的阶数,α=pπ/2是FrFT的旋转角度,
| $ \mathit{\boldsymbol{x}}(t) = \int_{ - \infty }^{ + \infty } {{\mathit{\boldsymbol{X}}_p}} (u){\mathit{\boldsymbol{K}}_{ - p}}(u, t){\rm{d}}u $ | (7) |
由式(6)可以看出α只出现在三角函数中,因此,只需考虑p∈(-2, 2]或α∈(-π, π]即可。当p=0时,X0(u)=x(t),信号x(t)的0阶分数阶傅里叶变换为其原始信号;当p=1时,X1(u)=
FrFT可以理解为chirp基分解,FrFT核函数实际上是一组调频率为cotα(α=pπ/2)的chirp信号,分数阶傅里叶域由该组完备正交基所表征,通过改变旋转角度α可以得到不同调频率的基。一旦所需要提取的线性调频(LFM)信号与某组基的调频率一致,则该信号必然在该组基中的某个基上形成一个函数,在别的基上则为0。这说明LFM信号在该分数阶傅里叶变换域上具有很好的时频聚集性。由于解调后的轴承急变速过程中振动信号非常接近多分量LFM信号,因此适合利用单阶FrFT滤波对其进行处理。
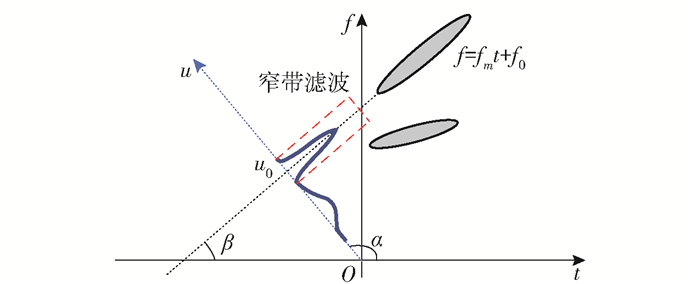
具有两个LFM分量的信号时频分布如图 2所示。其中一个分量(其斜率为fm,纵轴上的截距为f0)与时间轴之间的夹角为β,分数阶傅里叶变换可以解释为信号在时频平面内绕原点旋转任意角度后所构成的分数阶域上的表示, 即只要FrFT的旋转角度α与β正交,该LFM信号在分数阶傅里叶域上的投影就集中在u0一点。此时的α为FrFT变换最佳角度,p0=2α/π为最佳FrFT阶次。以u0为中心再对其进行滤波,经过-p0阶逆变换实现信号的提取,这样在多分量的情况下将LFM信号实现了信号分离。
|
图 2 双分量LFM信号单阶FrFT滤波 Fig.2 Single-order FrFT filtering of an LFM signal with two components |
采用单阶FrFT滤波提取LFM分量的关键在于准确确定最佳阶次p0和分数阶域聚集位置u0两个参数。当前在轴承故障诊断领域,确定FrFT滤波参数的常用方法是峰值搜索[15]。峰值搜索的方法是按照一定步长Δp对信号连续进行p∈[0, 2]的FrFT,如果信号具有LFM特性,就会在分数阶域坐标u和分数阶次p构成的(p, u)平面内出现峰值,在该平面内进行峰值二维搜索,就能确定该LFM信号的FrFT最佳阶次p0和相应分数阶域聚集位置u0。
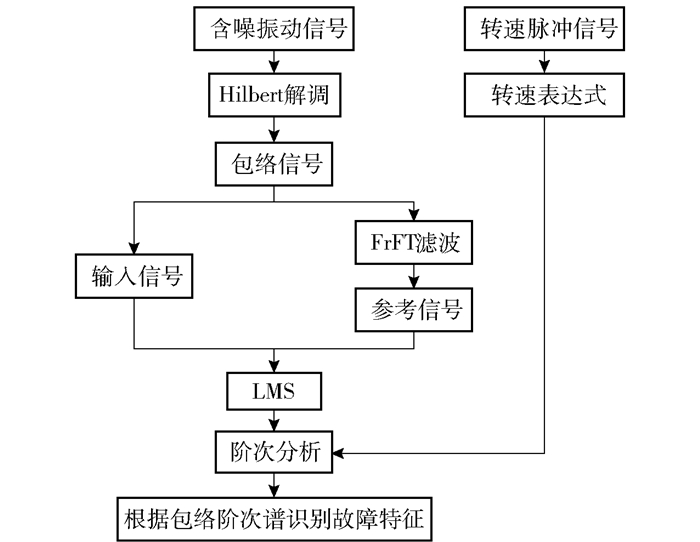
2 基于FrFT和LMS的故障诊断方法LMS自适应滤波的重点在于参考信号的选择,参考信号只在与噪声或故障源相关时才可实现良好的滤波效果。在目前已有的方法中,参考信号往往从噪声角度考虑,通过在特定位置加装振动传感器,收集噪声源信号或健康轴承振动信号作为参考信号进行自适应滤波。由于实际上满足这一要求的参考点并不是在每个机械设备上都存在,因此本文提出一种基于FrFT滤波和LMS降噪的故障诊断方法。由于故障一倍频能量往往最高,受干扰较小,通过峰值搜索FrFT在(p, u)平面找出的峰值往往对应于故障一倍频的最佳阶次p0和相应分数阶域聚集位置u0,因而据此进行FrFT滤波,将得到的滤波信号作为LMS算法中仅与故障源相关的参考信号,而不需要额外加装传感器采集参考信号。利用该方法的故障诊断流程如图 3所示,具体实现过程如下。
|
图 3 方法流程图 Fig.3 Flow chart of the proposed method |
1) 同步采集故障轴承振动信号和转速信号。将原始含噪振动信号Hilbert解调后得到的包络信号用于后续分析;对转速脉冲信号进行拟合得到同步转速表达式,用于阶次分析。
2) 对包络振动信号进行峰值搜索FrFT,将在(p, u)平面搜索得到的峰值设为故障一倍频对应的的最佳阶次p0和相应分数阶域聚集位置u0,进行单阶FrFT滤波。
3) 将FrFT滤波得到的信号,即故障一倍频,作为LMS中的参考信号,原始包络信号作为LMS中的输入信号,进行LMS自适应滤波,得到仅和故障相关的信号成分。
4) 依据步骤1)中由转速脉冲信号拟合得到的同步转速表达式,对LMS滤波后的信号等角度重采样后进行阶次分析,将包络阶次谱中的突出特征与已知轴承故障阶次对比,诊断故障类型。
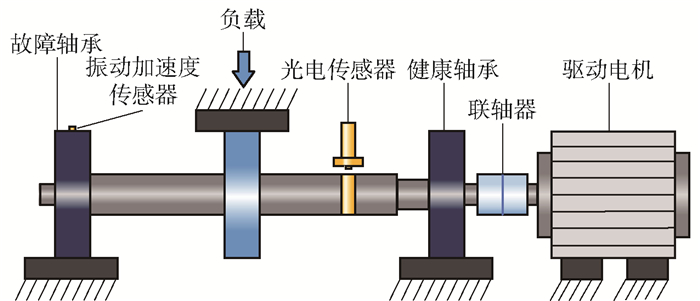
3 试验分析 3.1 试验设置为了验证所提方法的有效性,设计试验对故障滚动轴承进行测试,滚动轴承由电机驱动,同步采集轴承在设定变转速条件下的转速脉冲信号和振动加速度信号。试验台如图 4所示,加速度传感器安装在故障轴承轴承座上方,用于测量加速度信号;光电转速传感器安装在距附于轴上的反射片约100 mm处,用于测量转速脉冲信号。所用试验滚动轴承类型为NU205EM,通过线切割技术将健康滚动轴承人为植入微弱局部损伤。故障轴承的详细参数如表 1所示。
|
图 4 试验台 Fig.4 Test rig |
| 下载CSV 表 1 故障轴承参数 Table 1 Parameters of the fault bearing |
为了采集变转速条件下故障轴承的振动信号和速度信号,通过变频器使驱动电机匀变速运转,采集得到轴承在匀变速工况下运行的信号。试验采样频率为20 kHz。
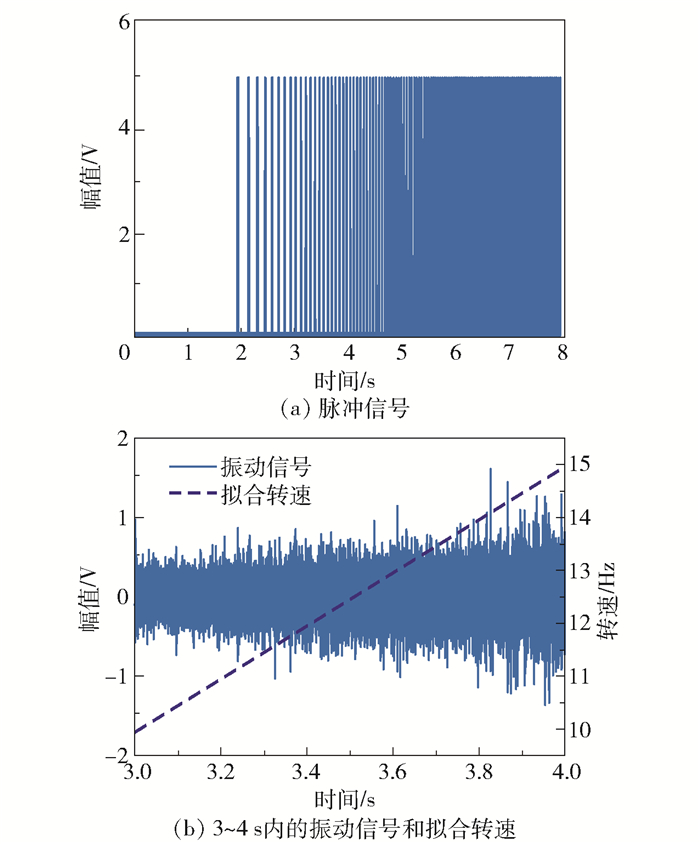
3.2 内圈故障信号分析通过线切割技术在健康滚动轴承内圈加工出深度0.15 mm、宽度0.2 mm的切痕,对该内圈故障轴承在变转速工况下的转速和振动信号进行同步采样,采集到的转速脉冲信号如图 5(a)所示。由转速脉冲信号进行转速曲线拟合,得到转速曲线和转速表达式。由于采集时间过长,以及信号采集过程中电机速度变化不完全稳定,选取速度变化相对稳定的时间范围内的信号进行分析。本文试验选择3~4 s时间段内的信号进行分析。图 5(b)展示了采集到的3~4 s内的含噪振动加速度信号,通过同步脉冲信号拟合得到的转速表达式为f(t)=5.016t-5.105。
|
图 5 内圈故障轴承采集信号 Fig.5 Collected signals from the inner race fault bearing |
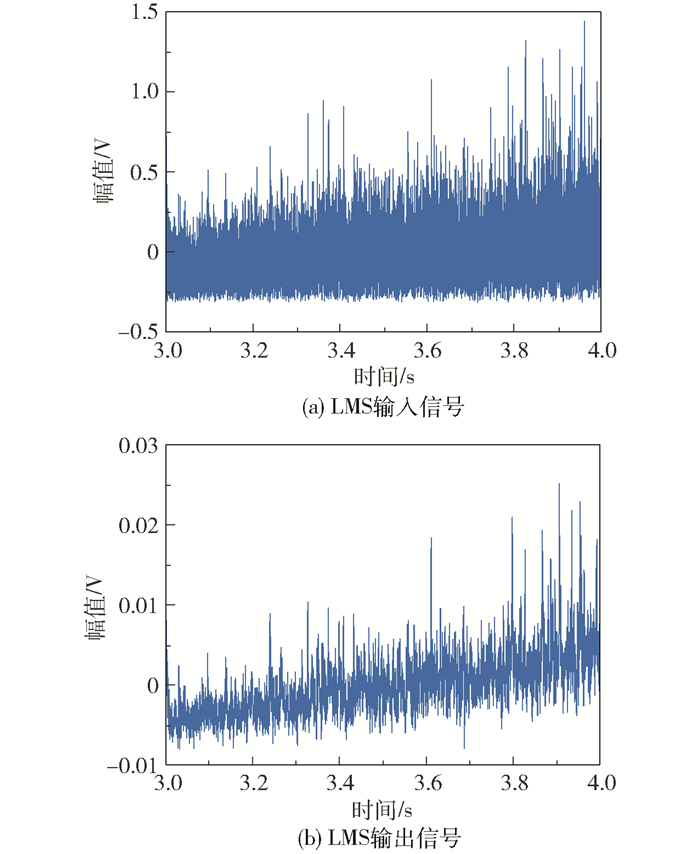
将含噪振动加速度信号经Hilbert解调得到包络信号。按照固定步长Δp=0.000 1对包络信号连续进行p∈[0, 2]的FrFT,在分数阶域坐标u和分数阶次p构成的(p, u)平面内进行峰值点的二维搜索,得到峰值点对应的最佳阶次p0和分数阶域聚集位置u0分别为p0=1.001 1和u0=10 088。在p0对应的分数阶域内以u0为滤波中心进行窄带滤波,再进行-p0阶的FrFT逆变换,得到FrFT滤波后的时域信号。以原始包络信号为LMS算法的输入信号,FrFT滤波后的信号为LMS算法的参考信号,进行自适应滤波,滤波结果如图 6所示,可看到明显的降噪效果。
|
图 6 内圈故障信号降噪前后对比 Fig.6 Comparison before and after noise reduction of the inner race fault bearing signal |
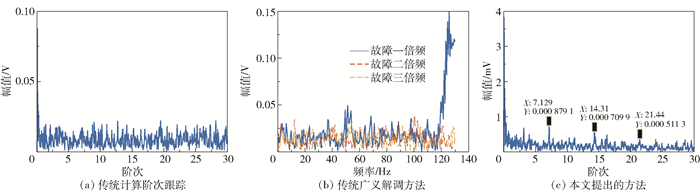
将LMS自适应滤波后的结果依据拟合得到的转速表达式进行重采样并作阶次分析,结果如图 7(c)所示,可清晰看到在阶次7.129、14.31和21.44处有明显峰值,符合预设内圈故障特征阶次7.15及其倍频。将其与常用的计算阶次跟踪方法和广义解调方法作对比,结果分别示于图 7(a)和图 7(b),其中广义解调方法内圈故障对应特征频率为36.5 Hz及其倍频,可以看出在图 7(a)和(b)中均找不到明显的故障特征。为了更直观地展示所提方法的优势,将3种方法分别对于故障前三倍频的提取精度误差er列于表 2,其计算公式如式(8)所示,其中vt为理论故障特征,vc为采集故障特征。可以看出所提方法实现了较高的诊断精度。对比结果表明所提出的故障诊断方法可以有效降噪,凸显故障特征,实现变转速下的轴承故障诊断。
| $ {e_{\rm{r}}} = \frac{{\left| {{v_{\rm{t}}} - {v_{\rm{c}}}} \right|}}{{{v_{\rm{t}}}}} \times 100\% $ | (8) |
|
图 7 内圈故障轴承信号处理结果对比 Fig.7 Comparison of the processing results for the inner ring fault bearing signal |
| 下载CSV 表 2 内圈故障前三倍频精度误差 Table 2 Accuracy errors for the first three harmonics of the inner fault characteristics |
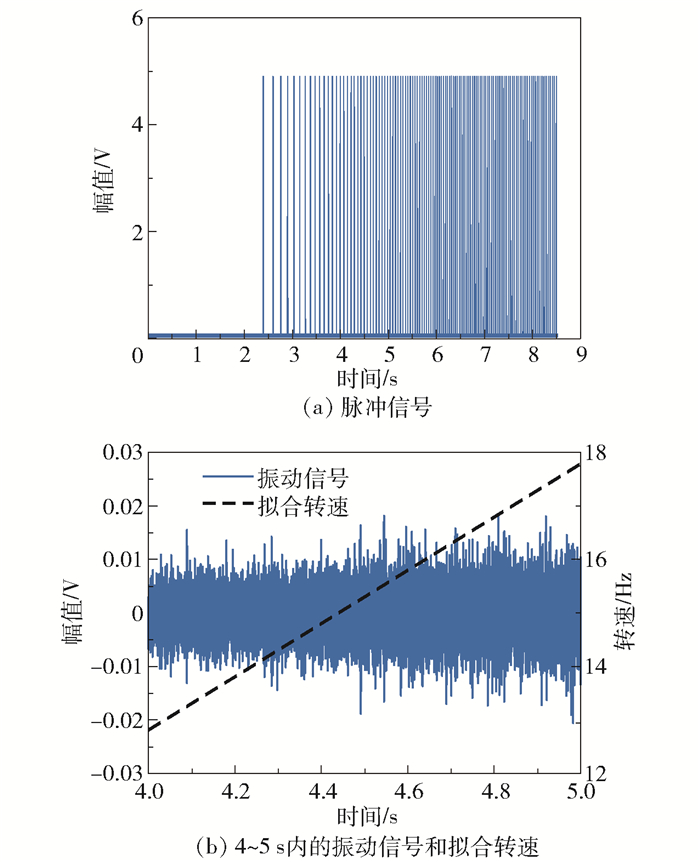
通过线切割技术在健康滚动轴承外圈加工出深度0.08 mm、宽度0.12 mm的切痕,对该外圈故障轴承在变转速工况下的转速和振动信号进行同步采样,采集到的转速脉冲信号如图 8(a)所示。由转速脉冲信号进行转速曲线拟合,得到转速曲线和转速表达式。选择4~5 s时间段内的信号进行分析,图 8(b)展示了采集到的4~5 s内的含噪振动加速度信号,通过同步脉冲信号拟合得到的转速表达式为f(t)=4.975t-7.09。由振动信号幅值可以看出该组数据对应的故障更微弱。
|
图 8 外圈故障轴承采集信号 Fig.8 Collected signals from the outer race fault bearing |
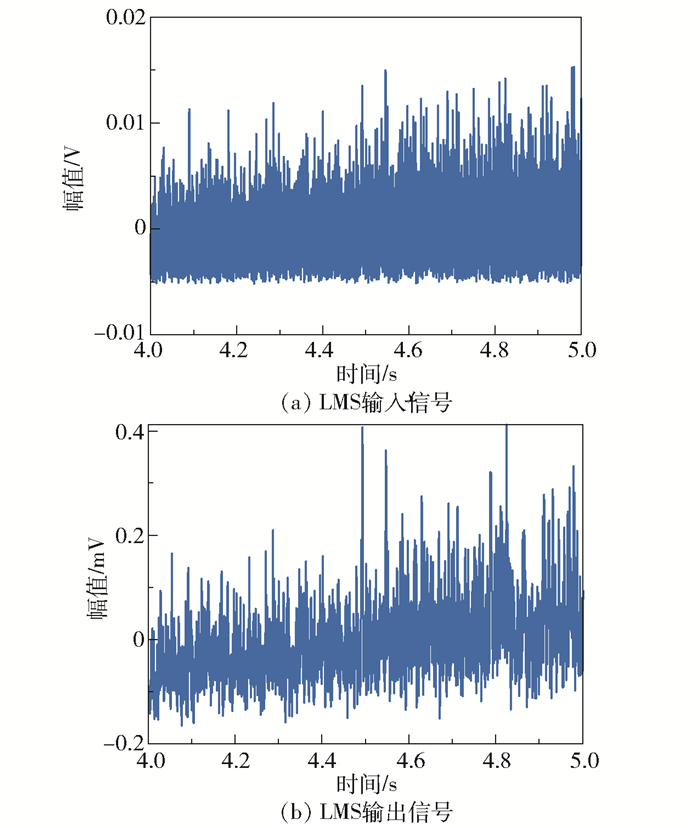
将含噪振动加速度信号经Hilbert解调得到包络信号。按照固定步长Δp=0.000 1对包络信号连续进行p∈[0, 2]的FrFT,在分数阶域坐标u和分数阶次p构成的(p, u)平面内进行峰值点的二维搜索,得到峰值点对应的最佳阶次p0和分数阶域聚集位置u0分别为p0=1.000 8和u0=10 074。在p0对应的分数阶域内以u0为滤波中心进行窄带滤波,再进行-p0阶的FrFT逆变换,得到FrFT滤波后的时域信号。以原始包络信号作为LMS算法的输入信号,FrFT滤波后的信号作为LMS算法的参考信号,进行自适应滤波,滤波结果如图 9所示,可以看到明显的降噪效果。
|
图 9 外圈故障信号降噪前后对比 Fig.9 Comparison before and after noise reduction of the outer race fault bearing signal |
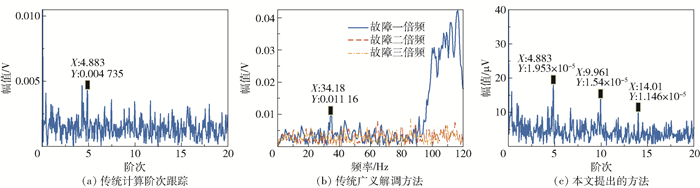
将LMS自适应滤波后的结果依据拟合得到的转速表达式进行重采样并作阶次分析,结果如图 10(c)所示,可清晰地看到在阶次4.883、9.961和14.01处有明显峰值,基本符合预设外圈故障特征阶次4.85及其倍频。将其与常用的计算阶次跟踪方法和广义解调方法进行对比,结果分别示于图 10(a)和(b),其中广义解调方法外圈故障对应特征频率为34.4 Hz及其倍频,可以看出图 10(a)中有较明显的故障一倍频,但其附近存在一些干扰,图 10(b)中同样可以找到微弱的故障一倍频,然而均无法找到更高的倍频。表 3展示了上述3种方法分别对于故障前三倍频的提取精度误差,可以看出本文所提方法可以有效提取故障前三倍频,精度误差在可接受范围内,相比于另外两种传统处理变速信号的方法具有更强的故障特征提取能力。
|
图 10 外圈故障轴承信号处理结果对比 Fig.10 Comparison of the processing results for the outer ring fault bearing signal |
| 下载CSV 表 3 外圈故障前三倍频精度误差 Table 3 Accuracy errors for the first three harmonics of the outer fault characteristics |
本文提出一种基于FrFT滤波和LMS降噪的故障诊断方法来对变转速工况下的滚动轴承振动信号进行降噪,进而提取非平稳故障特征。该方法通过分数阶傅里叶变换,利用信号在适当的分数阶傅里叶域内有最佳的能量聚集性,以及故障一倍频能量通常最大的特性,进行峰值搜索FrFT,按照搜索得到的最佳阶次和分数阶域聚集位置进行FrFT滤波,得到的滤波信号作为LMS算法中仅与故障源相关的参考信号,再进行LMS自适应滤波。该方法克服了LMS算法对辅助设备的依赖,使其具有更广的应用范围,且降噪过程不影响目标轴承故障冲击成分,能够实现变转速轴承信号的有效降噪,并成功提取非平稳故障特征。与变转速故障诊断领域常见的计算阶次跟踪和广义解调方法对比结果表明,本文所提方法可以成功提取故障前三倍频,具有明显的优势。
| [1] |
LI G Z, TANG G, LUO G G, et al. Underdetermined blind separation of bearing faults in hyperplane space with variational mode decomposition[J]. Mechanical Systems and Signal Processing, 2019, 120: 83-97. DOI:10.1016/j.ymssp.2018.10.016 |
| [2] |
QIN C R, WANG D D, XU Z, et al. Improved empirical wavelet transform for compound weak bearing fault diagnosis with acoustic signals[J]. Applied Sciences, 2020, 10(2): 682. DOI:10.3390/app10020682 |
| [3] |
HA J M, YOUN B D, OH H, et al. Autocorrelation-based time synchronous averaging for condition monitoring of planetary gearboxes in wind turbines[J]. Mechanical Systems and Signal Processing, 2016, 70-71: 161-175. DOI:10.1016/j.ymssp.2015.09.040 |
| [4] |
张丹, 崔善政, 隋文涛, 等. 基于IMF和预测滤波的轴承故障诊断方法[J]. 组合机床与自动化加工技术, 2016(8): 115-117, 136. ZHANG D, CUI S Z, SUI W T, et al. Diagnosis method for bearings based on IMF and prediction filtering[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(8): 115-117, 136. (in Chinese) |
| [5] |
张盈盈, 潘宏侠, 郑茂远. 自适应噪声抵消技术在轴承故障诊断中的应用[J]. 煤炭技术, 2010, 29(12): 21-23. ZHANG Y Y, PAN H X, ZHENG M Y. Application of adaptive noise cancellation technology in rolling bearing fault diagnosis[J]. Coal Technology, 2010, 29(12): 21-23. (in Chinese) |
| [6] |
张西宁, 周融通, 郭清林, 等. 局部倒频谱编辑方法及其在齿轮箱微弱轴承故障特征提取中的应用[J]. 西安交通大学学报, 2019, 53(12): 1-9. ZHANG X N, ZHOU R T, GUO Q L, et al. Local cepstral editing procedure with applications to slight gearbox bearing fault feature extraction[J]. Journal of Xi'an Jiaotong University, 2019, 53(12): 1-9. (in Chinese) |
| [7] |
朱敏, 段志善, 郭宝良, 等. CEEMDAN结合LMS算法在轴承信号降噪中的应用[J]. 噪声与振动控制, 2018, 38(2): 144-149. ZHU M, DUAN Z S, GUO B L, et al. Application of CEEMDAN combined with LMS algorithm in signal de-noising of bearings[J]. Noise and Vibration Control, 2018, 38(2): 144-149. (in Chinese) DOI:10.3969/j.issn.1006-1355.2018.02.028 |
| [8] |
杨晓雨, 荆双喜, 罗志鹏. 基于LMS和Fast-Kurtogram的滚动轴承早期故障诊断[J]. 噪声与振动控制, 2019, 39(1): 172-176. YANG X Y, JING S X, LUO Z P. Early fault diagnosis of rolling bearings based on LMS and Fast-Kurtogram[J]. Noise and Vibration Control, 2019, 39(1): 172-176. (in Chinese) |
| [9] |
TANG G, WANG Y T, HUANG Y J, et al. Compound bearing fault detection under varying speed conditions with virtual multi-channel signals in angle domain[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(8): 5535-5545. DOI:10.1109/TIM.2020.2965634 |
| [10] |
BORGHESANI P, RICCI R, CHATTERTON S, et al. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 23-35. DOI:10.1016/j.ymssp.2012.09.014 |
| [11] |
CHENG W D, GAO R X, WANG J J, et al. Envelope deformation in computed order tracking and error in order analysis[J]. Mechanical Systems and Signal Processing, 2014, 48(1/2): 92-102. |
| [12] |
张袁元, 李舜酩, 胡伊贤, 等. LMS方法的改进及联合EEMD在振动信号去噪中的应用[J]. 振动与冲击, 2013, 32(20): 61-66. ZHANG Y Y, LI S M, HU Y X, et al. Improvement of LMS method and its application combined with EEMD in vehicle vibration signal denoising[J]. Journal of Vibration and Shock, 2013, 32(20): 61-66. (in Chinese) |
| [13] |
ALMEIDA L B. The fractional Fourier transform and time-frequency representations[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3084-3091. |
| [14] |
LI X, MA Z Q, KANG D, et al. Fault diagnosis for rolling bearing based on VMD-FRFT[J]. Measurement, 2020, 155: 107554. |
| [15] |
ZHENG L Y, SHI D M. Maximum amplitude method for estimating compact fractional Fourier domain[J]. IEEE Signal Processing Letters, 2010, 17(3): 293-296. |








