2. 中国科学院 广州能源研究所 中国科学院天然气水合物重点实验室, 广州 510640;
3. 中国科学院 广州天然气水合物研究中心, 广州 510640;
4. 广东省新能源和可再生能 源研究开发与应用重点实验室, 广州 510640;
5. 中国科学院大学, 北京 100049
2. Key Laboratory of Gas Hydrate, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640;
3. Guangzhou Center for Gas Hydrate Research, Chinese Academy of Sciences, Guangzhou 510640;
4. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640;
5. University of Chinese Academy of Sciences, Beijing 100049, China
天然气水合物是以CH4、C2H6、CO2等气体分子为客体,以H2O分子为主体,在低温高压下形成的一种笼型晶体化合物,其中主体分子以氢键相互连接形成不同的笼型孔穴,客体分子占据孔穴。天然气水合物的晶体结构主要包括Ⅰ型(SⅠ)、Ⅱ型(SⅡ)和H型(SH)。Ⅰ型水合物晶胞是由2个512小孔穴和6个51262大孔穴总共46个H2O分子形成的体心立方结构;Ⅱ型水合物晶胞是面心立方结构,包含136个H2O分子,由8个51264大孔穴和16个512小孔穴组成;H型水合物晶胞是简单的立方结构,包含34个H2O分子,晶胞中有3种不同的孔穴,即3个512孔穴、2个435663孔穴和1个51268孔穴。在自然界中天然气水合物主要以SⅠ晶体结构存在,客体分子主要为CH4。由于具有储量大、热值高、无污染等优点,天然气水合物作为21世纪的一种新能源,其开采研究对于我国后续能源的可持续发展具有重要意义。目前,天然气水合物的开采方法主要有热激法、降压法和化学试剂法,各个方法均有一定的局限,因此开采方法的优化,以及新型开采方法的研发是天然气水合物开采技术研究的重点。CO2置换开采水合物方法是一种新型的开采方法,在从水合物中置换出天然气的同时注入CO2从而生成CO2水合物。该方法在开采出水合物资源的同时存储CO2,可有效地减少碳排放,降低温室效应[1]。同时,CO2水合物的形成可有效防止水合物分解引发的地质问题。因此,CO2置换开采天然气水合物技术被认为是可用于水合物开采和减少碳排放的具有巨大应用潜力的一种手段。
实验和理论研究表明,注入CO2置换天然气水合物中的CH4是可行的[2]。从热力学上看,CO2水合物体系的平衡条件要比CH4水合物体系的平衡条件温和[3]。从动力学上看,当温度为250 K时,CO2置换CH4水合物过程的吉布斯自由能ΔG是负值,这意味着置换反应是自发进行的[4]。Yuan等[5]利用三维反应器对CO2置换CH4水合物过程的有利条件进行研究,发现具有游离气的水合物储层适合置换开采。对CO2置换CH4水合物过程的微观分析和组分测量表明,置换主要发生在水合物相中[6],CO2水合物和CH4水合物同时存在于水合物中,置换过程不存在CH4水合物的解离[7]。有部分研究表明CH4水合物中只有51264笼中的CH4被置换,因此置换效率较低[8]。为提高置换效率,探究过程中的置换机理成为CO2置换CH4水合物技术研究的重点。目前,宏观实验和微观测试的研究能够获得置换过程的热力学和动力学特性,但还不足以解释置换机理。计算机模拟是在微观尺度上揭示置换机理的一种有效方法。近年来,研究者们将分子动力学(molecular dynamics,MD)模拟用于研究CO2置换CH4水合物过程的置换机理,模拟结果表明,置换过程可以分为3个步骤[9]: 首先打破水合物笼子,然后CH4分子跑出笼子,同时CO2分子进入空笼并占据笼子进行置换。Liu等[10]利用MD模拟发现置换出的CH4分子在形成气泡的过程中并没有出现漆膜,而且CO2分子的存在能够促使CH4分子形成气泡,防止CH4重新生成水合物,从分子角度阐述了CO2的置换机理。MD模拟能从分子尺度解析置换的动态过程,量子力学(quantum mechanics,QM)模拟则能从量子尺度,通过从头算(Ab initio calculation)以及密度泛函理论(density functional theory,DFT)的方法对水合物主客体分子间的电子效应进行分析,从量子层面解释置换机理[11]。Geng等[12]利用MD模拟和QM模拟对CH4、CO2以及CH4-CO2水合物的稳定性进行研究,通过分子尺度的径向分布函数、均方位移、扩散系数以及量子尺度的结合能的对比分析,发现CH4-CO2混合水合物的稳定性最高,此结果与Ota等[13]的实验结果相一致。Liu等[4]利用从头算方法对CO2取代CH4占据水合物笼子的结合能变化及热力学特性进行研究,发现CO2占据51262笼在热力学上的有利性。
由上述研究可知,水合物中主、客体分子对水合物的稳定性具有重要的影响。为更深入地阐述CO2置换CH4水合物过程的本质,本文采用DFT方法对水合物中主、客体双分子聚体之间的相互作用进行模拟,通过对称性匹配微扰理论(symmetry adapted perturbation theory,SAPT)进行能量分析,解析主、客体相互作用中静电、色散、诱导和交换4种相互作用各自的贡献。同时计算了波函数信息,分析了约化密度梯度函数(reduced density gradient,RDG)、独立梯度模型(independent gradient model,IGM)、静电势等参数,探讨主、客体对水合物笼子稳定性影响的作用机理,为深层次地阐述置换机理提供理论依据。
1 模型及计算方法本文利用DFT方法对水合物中主、客体分子聚体,即H2O-H2O、H2O-CH4、H2O-CO2双分子聚体进行研究,针对它们的几何结构、相互作用能量、相互作用方式进行计算模拟。模拟通过几何优化确定双分子聚体的最优结构,然后计算单点能,采用式(1)计算双分子聚体的相互作用能。
| $ \Delta {E_{{\rm{a}} - {\rm{b}}}} = {E_{{\rm{total }}}} - {E_{\rm{a}}} - {E_{\rm{b}}} $ | (1) |
式中,ΔEa-b表示双分子聚体中分子之间的相互作用能,a、b分别表示聚体中的分子;Etotal表示聚体的总能量;Ea和Eb分别表示双分子聚体中各个分子的能量。模拟结构优化及能量计算都在Gaussian16程序C.01版本[14]上进行。
在模拟中结构优化以二阶Møller-Plesset(MP2)在6-311+G(2d, 2p)基组下优化结构的结果为基准,该方法是水合物QM计算优化结构中较为精准的一种方法[15]。但该方法基于开发较早的理论进行计算,随着量子化学方法的发展,需要评估新的理论方法在双分子聚体计算中的优劣。因此,本文分别使用具有Grimme的DFT-D3(BJ)色散矫正的B3LYP泛函(B3LYP-D3)、DFT-D3色散矫正M062X泛函[16](M062X-D3)以及具有DFT-D2色散矫正的WB97XD[17] 和B97D[18]泛函在6-311+G(2d, 2p)基组下进行几何结构优化并计算频率,确保没有虚频。在金标准CCSD(T)/aug-CC-pVTZ计算水平下进行单点能计算,应用Boys等[19]的counterpoise (CP)技术进行基组叠加误差的矫正(BSSE)。由于aug-CC-pVTZ基组与CP矫正一起使用时,只需要50%的BSSE矫正能[20],因此我们在CCSD(T)/aug-CC-pVTZ水平下计算相互作用能时设E矫正=E原始+0.5×EBSSE。
本文首次采用高阶SAPT[21]对水合物中主、客体双分子聚体进行能量分解,评估双分子聚体相互作用中静电、色散、诱导和交换4种相互作用对主、客体相互作用的贡献,以及影响置换过程的最主要的相互作用方式。整个SAPT计算都在PSI4程序[22]上进行。同时在几何优化后的结构的基础上,使用Multiwfn程序[23]计算波函数信息。通过RDG分析(也称为non-covalent interaction,NCI分析)[24]进行弱相互作用的可视化研究。采用IGM[25]对弱相互作用的强度进行分析。通过静电势分析获得静电作用在CO2置换CH4水合物过程中的影响方式。
2 结果与讨论 2.1 主、客体双分子聚体结构优化和相互作用能水合物的晶体结构主要由主体分子和客体分子组成的笼子构建而成,其中主体分子与客体分子间的相互作用决定笼子的稳定性。在CO2置换CH4水合物过程中,水合物笼子的主体H2O分子、客体CH4分子和置换的CO2分子之间的相互作用影响着整个置换过程。本文采用不同的泛函在6-311+G(2d, 2p)基组下进行结构优化,然后采用CCSD(T)/aug-CC-pVTZ水平计算相互作用能。模拟优化得到的H2O-H2O、H2O-CH4、H2O-CO2双分子聚体的几何构型如图 1所示,双分子聚体相互作用能计算结果如表 1所示。从表 1中可以看出,经B3LYP-D3泛函优化后计算得到的双分子聚体的能量相比于M062X-D3、WB97XD、B97D这3个泛函的计算结果,更接近于基准MP2函数的计算结果,表明B3LYP-D3泛函更适合用于描述H2O-H2O、H2O-CH4、H2O-CO2之间的相互作用。由于基准MP2函数计算时间较长[26],因此在B3LYP-D3/6-311+G(2d, 2p)水平下进行CO2置换CH4水合物过程的几何结构优化。
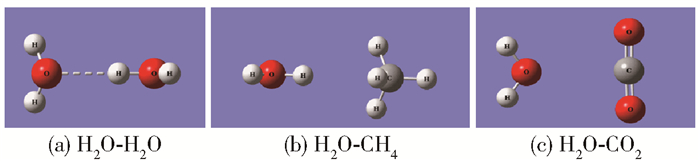
|
图 1 双分子聚体的优化结构 Fig.1 Optimized structures of dimers |
| 下载CSV 表 1 H2O-H2O、H2O-CH4、H2O-CO2双分子聚体相互作用能 Table 1 Interaction energies of H2O-H2O, H2O-CH4, H2O-CO2 dimers |
在B3LYP-D3/6-311+G(2d, 2p)水平下进行的3种双分子聚体结构优化的基础上,分别利用B3LYP、B3LYP-D3、M062X、M062X-D3、WB97XD、B97D、MP2等方法在6-311+G(2d, 2p)基组下进行双分子聚体相互作用能的计算,并与CCSD(T)/aug-CC-pVTZ水平下的计算结果进行对比,如表 2所示。从表 2可以看出,相比于其他计算水平,M062X/6-311+G(2d, 2p)水平下计算获得的分子间相互作用能与CCSD(T)/aug-CC-pVTZ水平下的计算结果最接近,表明其计算精度较其他方法的要高。CCSD(T)/aug-CC-pVTZ水平主要用于计算小分子单体,对于大分子体系计算较为困难[27],因此,M062X/6-311+G(2d, 2p)水平是CO2置换CH4水合物过程的QM研究的较优计算结合能参数。
| 下载CSV 表 2 不同计算水平下的双分子聚体相互作用能 Table 2 Interaction energies of dimers for different calculation levels |
从图 1、表 1和表 2可以看出,在H2O-H2O聚体中,不同H2O分子中的H原子与O原子由氢键连接形成相互作用,相互作用能为-21.05 kJ/mol。文献[28]对氢键进行了系统分类,指出弱氢键相互作用能小于-10.46 kJ/mol时,相互作用由静电和色散作用主导;“weak-to-medium”氢键相互作用能在-10.46~-58.60 kJ/mol时,相互作用由静电作用主导;中氢键相互作用能在-46.04~-62.79 kJ/mol之间时,相互作用由静电作用主导;强氢键相互作用能大于-62.79 kJ/mol时,相互作用由静电和感应作用主导。因此H2O分子中H原子与相邻的H2O分子中O原子间的相互作用介于弱氢键相互作用与中氢键相互作用之间。在H2O-CH4聚体中,H2O分子中的H与CH4中的C形成微弱的吸引作用,相互作用能为-4.06 kJ/mol。在H2O-CO2聚体中,H2O中的O原子与CO2中的C原子相互作用,相互作用能为-12.18 kJ/mol。可以看出H2O分子之间的相互作用明显高于H2O-CH4和H2O-CO2,因此在水合物中H2O分子与客体分子之间相互作用偏弱,更倾向于与其他H2O分子相互作用形成笼子。并且与H2O-CH4相比,H2O-CO2具有更高的相互作用能,当形成笼型水合物时,则更利于笼子的聚集,得到的CO2水合物较CH4水合物更加稳定[4]。
2.2 主、客体双分子聚体相互作用中各项相互作用的贡献在化学体系中,弱相互作用为分子间或分子内的非化学键作用,包括范德华作用、pi-pi堆积作用、氢键、二氢键、卤键等。SAPT利用片段间的微扰将弱相互作用分解为静电能(Eelst)、交换能(Eexch)、色散能(Edis)和诱导能(Eind)4部分,从而从能量角度更深入地理解弱相互作用的本质。本文通过SAPT对CO2置换CH4水合物过程中主、客体双分子聚体的能量进行分析,解析主、客体相互作用中静电、色散、诱导和交换4种相互作用的贡献。H2O-H2O、H2O-CH4、H2O-CO2双分子聚体在不同SAPT计算水平下的相互作用能列于表 3。将其与CCSD/aug-CC-pVTZ水平下的相互作用能比较发现,在SAPT下,计算级别的提升并不一定会伴随计算精度的提升,并且加入δMP2项来考虑诱导和色散间的高阶耦合作用,加入(CCD)项以优化色散项并不会使得相互作用能的计算值更接近CCSD/aug-CC-pVTZ水平下的计算值。通过对比分析发现SAPT2+/aug-CC-pVDZ、SAPT2+/jun-CC-pVTZ和SAPT2/aug-CC-pVTZ水平下计算的相互作用能更接近CCSD/aug-CC-pVTZ水平下的计算结果,具有较高的计算精度,因此它们在分析H2O-H2O、H2O-CH4、H2O-CO2双分子聚体相互作用时更具优势。在Parker等[21]有关于效率计算的研究中指出SAPT2+/jun-CC-pVTZ水平耗时是SAPT2+/aug-CC-pVDZ和SAPT2/aug-CC-pVTZ水平的5倍以上。当进行小分子聚体计算时,耗时差异较小,当进行水合物笼体的相关研究时,耗时差异则较大。而在实际的水合物笼体计算中,SAPT2/aug-CC-pVTZ水平计算过程的临时文件占用几T的硬盘储存空间,存在因硬盘空间不足而使得计算终止的问题。因此,考虑到计算精度与计算时长,水合物在SAPT分析中较适合采用SAPT2+/aug-CC-pVDZ水平计算,同时SAPT2+/aug-CC-pVDZ水平是文献[21]提出的SAPT计算中的“银”标准,能够进行精准的能量分解研究。
| 下载CSV 表 3 不同SAPT计算水平下双分子聚体相互作用能 Table 3 Interaction energies of dimers for different SAPT calculation levels |
在SAPT方法中,弱相互作用能可以被分解为具有不同物理意义的组分,即ΔE=Eelst+Eexch+Eind+ Edis。其中,Eelst主要反映主客体之间的经典静电相互作用;Eexch表示在主客体中由电子的费米子行为引起的单体波函数以及反对称的重叠交换排斥作用;Eind描绘了诱导作用,包括极化以及两种单体之间的电荷转移;Edis是由主客体的电子之间的库仑相关性引起的色散贡献。分子占据笼子时,主、客体相互作用能的差异明显,为了阐明水合物中主、客体相互作用的电子性质并探究影响主客体间稳定性的最主要的相互作用形式,我们对H2O-H2O、H2O-CH4、H2O-CO2双分子聚体在SAPT2+/aug-CC-pVDZ计算水平下进行SAPT分析,结果见表 4。从表 4中可以发现相互作用能的负值是由于静电、诱导、色散3项的总和大于交换排斥项的贡献产生的,因此总的相互作用主要为吸引作用。为了考察各吸引作用对总吸引作用的贡献,更直观深入地理解主客体相互作用的性质,将表 4中的数据转化为每个吸引项的贡献分数C,如式(2)所示。
| $ C = \left( {\frac{{{E_X}}}{{{E_{{\rm{elst }}}} + {E_{{\rm{ind }}}} + {E_{{\rm{dis }}}}}}} \right) \times 100\% $ | (2) |
| 下载CSV 表 4 SAPT2+/aug-CC-pVDZ水平下计算的双分子聚体相互作用能物理分量 Table 4 The physical components of the interaction energy of the dimers calculated at the SAPT2+/aug-CC-pVDZ level |
其中EX表示Eelst、Eind或Edis。SAPT衍生的各相互作用对总吸引作用的贡献分数如图 2所示。从图中可以看出,在H2O-H2O聚体中静电作用占比为64.25%,即吸引作用主要是由静电作用引起的,而诱导和色散作用的影响较小,占比分别为19.53%和16.21%。在H2O-CH4聚体中静电作用占比为36.00%,低于色散作用的45.20%,即吸引作用主要是由色散作用引起的,而诱导作用占比仅为18.80%,对总的吸引作用影响较小。在H2O-CO2聚体中色散作用占比为29.62%,相比于H2O-CH4聚体中高的色散贡献下降15.58%,静电作用占比为59.38%,较H2O-CH4聚体增加23.38%。由此发现在双分子聚体中,随着相互作用能的增加,静电作用有上升趋势,色散作用则表现为下降,即静电作用占比与相互作用能大小成正比,色散作用占比与相互作用能大小成反比。因此,可以推断客体分子CO2和CH4与主体H2O分子作用时静电和色散相互作用占比的差异导致了两种客体分子形成水合物时结构和能量的差别。
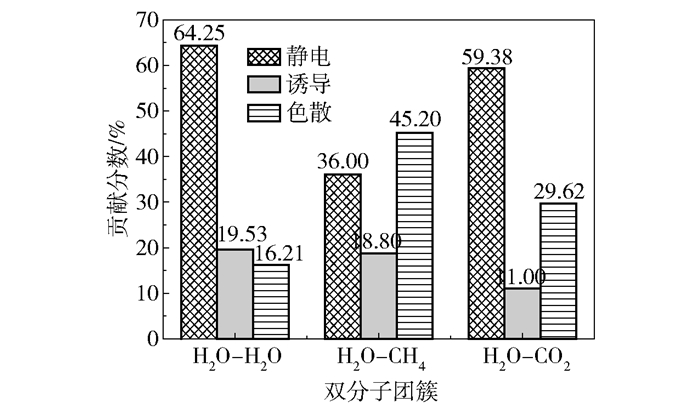
|
图 2 SAPT衍生的各相互作用对总吸引作用的贡献分数 Fig.2 The contribution percentage of each interaction derived from SAPT to the total attraction |
综上分析可知,在3种聚体的能量分解中H2O-H2O聚体的吸引作用主要由静电作用贡献,色散和诱导作用的影响较小。在H2O-CH4、H2O-CO2聚体的对比中发现,与H2O相互作用的分子由CH4转变为CO2时色散作用的影响减弱,静电作用的影响加强,表明了静电作用在CO2置换CH4中的重要地位。由此推断,增加静电作用是提升置换效率的有效方法,例如加入与H2O分子有较高静电作用的试剂分子,可以提高置换效率。
2.3 主、客体分子的静电势分析静电势V(r)(ESP)是由原子核和电子在周围空间每一点r处产生的分子间或分子内真实的物理特性,其值能够通过衍射实验以及计算的方法确定,计算公式为
| $ V(r) = \sum\limits_A {\frac{{{Z_A}}}{{{R_{A - r}}}}} - \int {\frac{{\rho (r){\rm{d}}{r^\prime }}}{{\left| {{r^\prime } - r} \right|}}} $ | (3) |
式中,ZA表示位于RA处原子核A所带的电荷数,ρ(r)表示分子的电子密度,r′表示距离r单位电子电荷增量距离。在任意点r上的V(r)反映了分子中每个核和每个电子在该点的贡献[29]。在任何给定的区域,V(r)是正还是负取决于原子核的正电荷或电子的负电荷在特定位置的主导性。V(r)是正的区域为亲核性,V(r)是负的区域为亲电性。计算过程中当电子密度为0.001 e/Bohr3(0.006 784 e/Å3)时,在分子表面绘制静电势等值面,如图 3所示。V(r)的最正值和最负值分别用Vmax和Vmin表示。图 3(a)为主体H2O分子的静电势等值面图,从图中可以看出H2O分子中H原子静电势的表面电位为正,且Vmax值为189.12 kJ/mol和189.20 kJ/mol,O原子静电势的表面电位为负, Vmin值为-140.44 kJ/mol。由此可以得出H2O-H2O聚体中H原子与O原子之间的静电势差达到329.64 kJ/mol。图 3(b)为客体CH4分子的静电势等值面图,可以看出H原子具有正的表面电荷,Vmax值为35.37 kJ/mol,Vmin点位于CH4的两个H原子之间。由图 3(a)和图 3(b)得出,H2O分子的Vmax与CH4分子的Vmin之差以及CH4分子的Vmax与H2O分子的Vmin之差分别为197.45 kJ/mol和175.81 kJ/mol,因此H2O分子的Vmax位点更利于同CH4分子的Vmin位点相互作用,即H2O分子中的H与CH4分子中的C形成相互作用,结果与图 1一致。图 3(c)为客体CO2分子的静电势等值面图,由图发现碳原子表面点位为正,Vmax值为118.08 kJ/mol,氧原子表面静电势为负,Vmin值为-48.14 kJ/mol。由图 3(a)和图 3(c)得出,在H2O-CO2聚体中H2O分子的Vmax与CO2分子的Vmin之差以及CO2分子的Vmax与H2O分子的Vmin之差分别为237.26 kJ/mol和258.52 kJ/mol,因此H2O分子的O原子更利于与CO2分子的C原子形成相互作用,这与图 1中的几何结构优化结果相同。在H2O-CO2聚体与H2O-CH4聚体的对比中,H2O-CO2聚体中两种分子的静电势差值(258.52 kJ/mol)高于H2O-CH4聚体的相应值(197.45 kJ/mol),但低于H2O-H2O聚体的329.64 kJ/mol,因此H2O与CO2相互作用的强度高于H2O与CH4分子,而低于H2O分子与H2O分子间的相互作用,这与相互作用能计算结果(表 1)的趋势相匹配。图 4为H2O-H2O、H2O-CH4、H2O-CO2双分子聚体的静电势表面穿透图,穿透位置与Vmax、Vmin的最大差值一致,对于H2O-H2O、H2O-CH4、H2O-CO2这3种聚体,其分子间静电势表面相互穿透距离分别为1.16 Å、0.45 Å、0.98 Å,相互作用强度与相互穿透距离的大小具有一致性,进一步验证了静电作用在H2O-H2O、H2O-CH4、H2O-CO2相互作用中的关键影响。
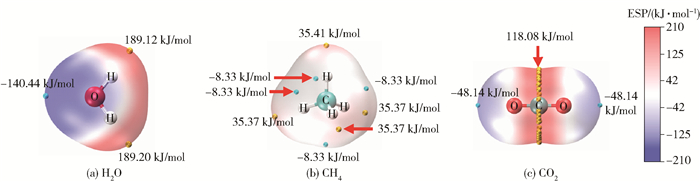
|
图 3 静电势等值面图 Fig.3 Isosurface diagrams of electrostatic potential |
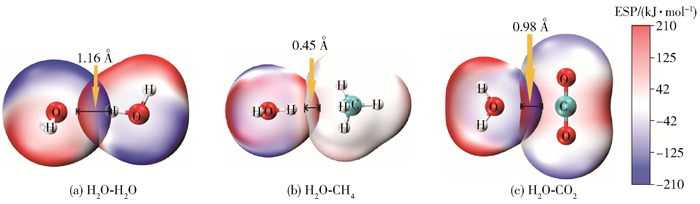
|
图 4 静电势表面穿透图 Fig.4 Surface penetration diagrams of electrostatic potential |
RDG分析基于电子密度及其降低的梯度,可定性鉴定和表征各种强度的弱相互作用。IGM理论则基于电子密度,能够识别和量化由于相互作用而导致的电子密度净梯度衰减,定义分子间相互作用的区域,从而直接表征分子间的相互作用。本文通过计算波函数信息,对主、客体分子进行RDG和IGM分析,定向研究主、客体分子对水合物笼子稳定性的影响机理。RDG分析是通过生成双分子聚体真实空间相应区域的梯度等值面来定位它们,通过这些区域的sign(λ2)ρ值来区分相互作用的种类,其中sign(λ2)函数是电子密度Hessian矩阵的第二大本征值λ2的符号,用以反映相互作用类型;弱相互作用临界点的ρ的数值和键的强度具有正相关性。sign(λ2)ρ值从0.05→0→-0.05逐渐减小,相互作用变化为强互斥作用(位阻作用)→范德华作用→强吸引作用(氢键、卤键等),在RDG图中表现为颜色从红色→绿色→蓝色的变化,如图 5所示。当sign(λ2)ρ>0时表现为互斥作用,sign(λ2)ρ<0时表现为吸引作用。从图 5中可以看出H2O-H2O聚体中H2O分子之间形成了较强的吸引作用,即氢键相互作用,而H2O-CH4、H2O-CO2聚体中分子间呈现出范德华相互作用。H2O-CO2聚体的范德华作用形成的sin(λ2)ρ峰值比H2O-CH4聚体的峰值更负,因此H2O分子与CO2分子之间的范德华作用高于H2O分子与CH4分子之间的范德华作用,这与客体分子和水合物笼子之间的相互作用趋势一致[30]。
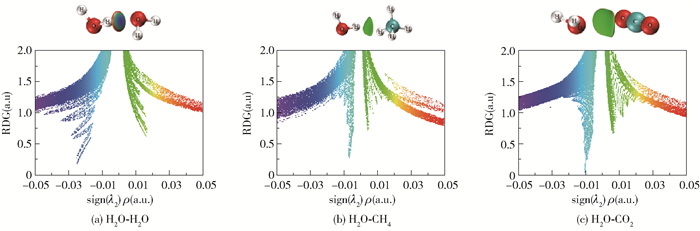
|
图 5 双分子聚体的RDG图 Fig.5 RDG diagrams of the dimers |
图 6为双分子聚体间的IGM图,图中的sign(λ2)ρ=0附近有左右两个峰,当sign (λ2)ρ < 0时,峰高表示吸引作用,当sign (λ2)ρ>0时,峰高则表示排斥作用。从图 6可以看出,吸引作用的峰尖比排斥作用的峰尖高,表明双分子聚体主要表现为吸引作用。由图 6(a)看出吸引作用的峰尖主要为蓝色,即H2O-H2O聚体是以氢键相互作用为主。由图 6(b)和图 6(c)看出吸引作用的峰尖主要为绿色,即H2O-CH4、H2O-CO2聚体中分子间呈现范德华力相互作用,该结果与RDG分析一致。在分子间相互作用区域,IGM方法定义的δg函数值与相互作用强度具有正相关性。对比3种双分子二聚体相互作用的δg值(图 6)发现δg, H2O-H2O>δg, H2O-CO2>δg, H2O-CH4。这与表 2中相互作用能的大小具有一致性,进一步验证了3种双分子二聚体相互作用间的差异。
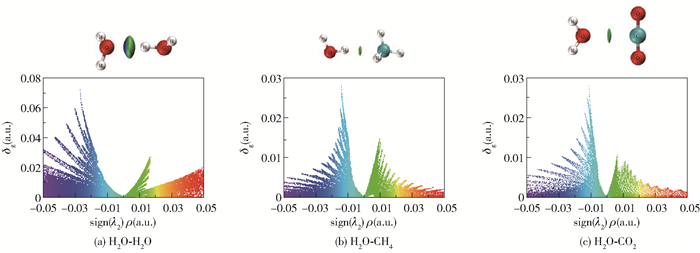
|
图 6 双分子聚体的IGM图 Fig.6 IGM diagrams of the dimers |
由上可知,RDG分析可表征主、客体分子之间的相互作用,IGM分析可获得主、客体分子之间的相互作用区域,判断相互作用大小,从而实现主、客体相互作用的定性及定量研究。本文研究从电子密度分析角度证实了H2O-H2O聚体是以氢键相互作用为主,H2O-CH4、H2O-CO2聚体中分子间是以范德华力相互作用为主。由此,主、客体双分子聚体分子间的相互作用是影响水合物笼子稳定性的关键因素。
3 结论(1) 对比不同DFT计算方法的精度,得到B3LYP-D3/6-311+G(2d, 2p)水平是CO2置换CH4水合物过程的QM研究的较优结构优化参数,M062X/6-311+G(2d, 2p)水平是CO2置换CH4水合物过程的QM研究的较优计算结合能参数。
(2) 结构优化与静电势分析结果表明,在CO2置换CH4水合物过程中,H2O分子的H原子与CH4分子的C原子形成相互作用,H2O分子的O原子与CO2分子的C原子形成相互作用;主体H2O分子与客体分子相互作用的强度低于H2O-H2O相互作用,因此主体H2O分子倾向于相互作用形成笼子;H2O-CO2相互作用的强度高于H2O-CH4相互作用,因此,当形成水合物笼子时,CO2水合物较CH4水合物更加稳定。
(3) 由静电、色散、诱导和交换4种相互作用的贡献分析得出,CO2置换CH4水合物过程中主、客体分子间的作用主要由静电作用贡献,色散和诱导作用的影响较小。置换过程中,客体分子由CH4转变为CO2时色散作用的影响减弱,静电作用的影响加强。
(4) RDG分析和IGM分析从电子密度角度证实了CO2置换CH4水合物过程中主体H2O分子之间以氢键相互作用为主,主、客体分子之间以范德华力相互作用为主。
由此,SPAT计算方法能较好地分析CO2置换CH4水合物过程中主、客体分子间的作用,研究结果表明静电作用是置换的关键因素,提高与H2O的静电作用是提升置换效率的有效方法。下一步我们将采用此QM方法用于天然气水合物分解机理的微观理论研究,与MD技术和微观实验结合分析CO2置换CH4水合物的动态过程,为天然气水合物技术的发展提供理论指导。
| [1] |
KOMATSU H, OTA M, JR SMITH R L, et al. Review of CO2-CH4 clathrate hydrate replacement reaction laboratory studies-properties and kinetics[J]. Journal of the Taiwan Institute of Chemical Engineers, 2013, 44(4): 517-537. DOI:10.1016/j.jtice.2013.03.010 |
| [2] |
GOEL N. In situ methane hydrate dissociation with carbon dioxide sequestration: current knowledge and issues[J]. Journal of Petroleum Science and Engineering, 2006, 51(3-4): 169-184. DOI:10.1016/j.petrol.2006.01.005 |
| [3] |
ANDERSON R, LLAMEDO M, TOHIDI B, et al. Experimental measurement of methane and carbon dioxide clathrate hydrate equilibria in mesoporous silica[J]. The Journal of Physical Chemistry B, 2003, 107(15): 3507-3514. DOI:10.1021/jp0263370 |
| [4] |
LIU J X, YAN Y J, XU J F, et al. Replacement micro-mechanism of CH4 hydrate by N2/CO2 mixture revealed by ab initio studies[J]. Computational Materials Science, 2016, 123: 106-110. DOI:10.1016/j.commatsci.2016.06.025 |
| [5] |
YUAN Q, SUN C Y, YANG X, et al. Recovery of methane from hydrate reservoir with gaseous carbon dioxide using a three-dimensional middle-size reactor[J]. Energy, 2012, 40(1): 47-58. DOI:10.1016/j.energy.2012.02.043 |
| [6] |
ZHOU X B, LIN F H, LIANG D Q. Multiscale analysis on CH4-CO2 swapping phenomenon occurred in hydrates[J]. The Journal of Physical Chemistry C, 2016, 120(45): 25668-25677. DOI:10.1021/acs.jpcc.6b07444 |
| [7] |
XU C G, YAN R, FU J, et al. Insight into micro-mechanism of hydrate-based methane recovery and carbon dioxide capture from methane-carbon dioxide gas mixtures with thermal characterization[J]. Applied Energy, 2019, 239: 57-69. DOI:10.1016/j.apenergy.2019.01.087 |
| [8] |
XU C G, CAI J, LIN F H, et al. Raman analysis on methane production from natural gas hydrate by carbon dioxide-methane replacement[J]. Energy, 2015, 79: 111-116. DOI:10.1016/j.energy.2014.10.068 |
| [9] |
QI Y X, OTA M, ZHANG H. Molecular dynamics simulation of replacement of CH4 in hydrate with CO2[J]. Energy Conversion and Management, 2011, 52(7): 2682-2687. DOI:10.1016/j.enconman.2011.01.020 |
| [10] |
LIU Y N, ZHAO L, DENG S, et al. Evolution of bubbles in decomposition and replacement process of methane hydrate[J]. Molecular Simulation, 2017, 43(13-16): 1061-1073. DOI:10.1080/08927022.2017.1359745 |
| [11] |
SHAO Y H, MOLNAR L F, JUNG Y, et al. Advances in methods and algorithms in a modern quantum chemistry program package[J]. Physical Chemistry Chemical Physics, 2006, 8(27): 3172-3191. DOI:10.1039/B517914A |
| [12] |
GENG C Y, WEN H, ZHOU H. Molecular simulation of the potential of methane reoccupation during the replacement of methane hydrate by CO2[J]. The Journal of Physical Chemistry A, 2009, 113(18): 5463-5469. DOI:10.1021/jp811474m |
| [13] |
OTA M, MOROHASHI K, ABE Y, et al. Replacement of CH4 in the hydrate by use of liquid CO2[J]. Energy Conversion and Management, 2005, 46(11/12): 1680-1691. |
| [14] |
FRISCH M, TRUCKS G, SCHLEGEL H, et al. Gaussian 16 Rev. C. 01[CP]. Wallingford: Gaussian Inc., CT., 2016.
|
| [15] |
THAKRE N, JANA A K. Physical and molecular insights to clathrate hydrate thermodynamics[J]. Renewable and Sustainable Energy Reviews, 2021, 135: 110150. DOI:10.1016/j.rser.2020.110150 |
| [16] |
ZHAO Y, TRUHLAR D G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals[J]. Theoretical Chemistry Accounts, 2008, 120(1): 215-241. |
| [17] |
CHAI J D, HEAD-GORDON M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections[J]. Physical Chemistry Chemical Physics, 2008, 10(44): 6615-6620. DOI:10.1039/b810189b |
| [18] |
GRIMME S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction[J]. Journal of Computational Chemistry, 2006, 27(15): 1787-1799. DOI:10.1002/jcc.20495 |
| [19] |
BOYS S F, BERNARDI F. The calculation of small molecular interactions by the differences of separate total energies[J]. Molecular Physics, 1970, 19(4): 553-566. DOI:10.1080/00268977000101561 |
| [20] |
BURNS L A, MARSHALL M S, SHERRILL C D. Comparing counterpoise-corrected, uncorrected, and averaged binding energies for benchmarking noncovalent interactions[J]. Journal of Chemical Theory and Computation, 2014, 10(1): 49-57. DOI:10.1021/ct400149j |
| [21] |
PARKER T M, BURNS L A, PARRISH R M, et al. Levels of symmetry adapted perturbation theory (SAPT). Ⅰ. Efficiency and performance for interaction energies[J]. The Journal of Chemical Physics, 2014, 149(9): 094106. |
| [22] |
PARRISH R M, BURNS L A, SMITH D G, et al. Psi41.1:an open-source electronic structure program emphasizing automation, advanced libraries, and interoperability[J]. Journal of Chemical Theory and Computation, 2017, 13(7): 3185-3197. DOI:10.1021/acs.jctc.7b00174 |
| [23] |
LU T, CHEN F W. Multiwfn: a multifunctional wavefunction analyzer[J]. Journal of Computational Chemistry, 2012, 33(5): 580-592. DOI:10.1002/jcc.22885 |
| [24] |
JOHNSON E R, KEINAN S, MORI-SÁNCHEZ P, et al. Revealing noncovalent interactions[J]. Journal of the American Chemical Society, 2010, 132(18): 6498-6506. DOI:10.1021/ja100936w |
| [25] |
LEFEBVRE C, RUBEZ G, KHARTABIL H, et al. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density[J]. Physical Chemistry Chemical Physics, 2017, 19(27): 17928-17936. DOI:10.1039/C7CP02110K |
| [26] |
AN T, ZHANG H, ZHANG Q, et al. Influence of CH4 and C3H8 molecules on stability of double-cage of sI clathrate hydrate[J]. Computational and Theoretical Chemistry, 2018, 1123: 128-134. DOI:10.1016/j.comptc.2017.11.019 |
| [27] |
RAGHAVACHARI K, TRUCKS G W, POPLE J A, et al. A fifth-order perturbation comparison of electron correlation theories[J]. Chemical Physics Letters, 1989, 157(6): 479-483. DOI:10.1016/S0009-2614(89)87395-6 |
| [28] |
EMAMIAN S, LU T, KRUSE H, et al. Exploring nature and predicting strength of hydrogen bonds: a correlation analysis between atoms-in-molecules descriptors, binding energies, and energy components of symmetry-adapted perturbation theory[J]. Journal of Computational Chemistry, 2019, 40(32): 2868-2881. DOI:10.1002/jcc.26068 |
| [29] |
MURRAY J S, POLITZER P. Molecular electrostatic potentials and noncovalent interactions[J]. WIREs Computational Molecular Science, 2017, 7(6): e1326. |
| [30] |
ROMÁN-PÉREZ G, MOAIED M, SOLER J M, et al. Stability, adsorption, and diffusion of CH4, CO2, and H2 in clathrate hydrates[J]. Physical Review Letters, 2010, 105(14): 145901. DOI:10.1103/PhysRevLett.105.145901 |








