氧化锆(ZrO₂)具有高熔点、高强度、耐腐蚀、低导热系数、强化学稳定性、宽禁带、高电阻率等特性^[1]，近年来，由于其卓越的机械和电气性能，以ZrO₂为基体的复合多功能材料成为研究热点，并已被用作气体传感器^[2]、固体燃料电池^[3]、高耐久性涂层^[4]、催化剂^[5]等方面。氧化锆的能带间隙E_g (~6 eV)和介电性能(相对介电常数ε_r约为25)表明其在栅极堆叠、动态存取存储器件和光学应用领域具有巨大的潜力，若叠加其高熔点、低导热、强稳定性、宽禁带并可与Si良好接触等性能^[6]，在金属氧化物半导体器件(MOS)领域中有完全取代绝缘栅SiO₂的可能性。

晶体ZrO₂具有单斜(m)、四方(t)和立方(c)相等多种晶型^[6]，其中富氧环境的m相是其低温稳定相，1 205 ℃开始转变成t相，2 065 ℃开始转变为高温c相，在高于2 300 ℃时转变为液相(L)。m相中Zr⁴⁺呈7个氧原子配位畸变；t相中Zr⁴⁺呈8个氧原子配位，但有两个不同的Zr—O键长；c相为与Zr—O键等长的Zr⁴⁺八配位的c萤石结构^[7]。在实验中常温下为了得到t相或c相ZrO₂，需要掺入稳定剂如CaO、Y₂O₃^[8]，通过掺杂阳离子，引入阴离子空穴来稳定t氧化锆(partial stable zirconia, PSZ)或c氧化锆(fully stabilized zirconia, FSZ)结构，在一般环境温度和压力下，Y₂O₃稳定ZrO₂(Y-stabilized zirconia, YSZ)在掺杂0~3%(摩尔分数，下同)Y₂O₃时以m相存在^[9]，掺杂2%~9%Y₂O₃时形成t相，掺杂4%~40%Y₂O₃时稳定于c相^[10]，Y₂O₃含量高于40%时发现生成具有化学计量Zr₃Y₄O₁₂的菱形δ-相，此时掺杂氧化锆(FSZ)结构主要表现为短程有序性^[11]。上述文献报道了ZrO₂及YSZ相关材料的性能及其改善(多数有关t相或c相ZrO₂的实验数据均是从YSZ中获取)，但对ZrO₂内部结构的稳定机理较少进行深入的理论分析，因此本文拟在前人工作的基础上，从第一性原理出发，运用密度泛函理论从原子尺寸角度对不同相的ZrO₂电子结构性质进行模拟计算，为新型多功能复合材料的设计与研制提供理论指导。

ZrO₂典型的m相空间群为P2₁/c，对称性为C2H-5(No.14)，α=γ=90°, β=100.054 8°；t相空间群为P4₂/mnc，对称性为D4H-15(No.137)，α=β=90°, γ=120°；c相空间群为Fm3m, 对称性为OH-5(No.225)，α=β=γ=90°。

计算主要采用Materials studio软件中的CASTEP模块^[12]完成，基于密度泛函理论(density functional theory，DFT)框架^[13]，分别以广义梯度近似(general gradient approximate, GGA)^[14]、GGA+U^[15]和杂化泛函(hybrid Becke three parameters hybrid exchange(B3)+ LYP correlation，hybrid B3LYP) ^[16] 3种方法计算，其中GGA的交换关联函数选择Perdew-Burke-Ernzerhof (PBE)函数^[17]，GGA+U方法中Zr的d电子U值(经验修正因电子相互作用引起的误差值)设置为2 eV；结构几何优化采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法^[18]，布里渊区积分采用以Γ点为中心的4×4×4 k点设置，计算中离子实(原子核+内层电子)与价电子之间的相互作用使用模守恒赝势(nom conserving)来描述，用于计算的Zr和O原子的价电子组态分别为Zr(4s² 4p⁶ 4d² 5s²)，O(2s² 2p⁴)，平面波截止能E_cut为750.0 eV；晶体优化自洽收敛标准设置为最大位移1.0×10^-3 nm, 最大内应力收敛标准0.05 GPa, 原子间的最大相互作用力0.03 eV/nm，结构的总体能量收敛小于1×10^-5 eV每原子。

按照设定的能量收敛参数，分别对三相晶胞结构进行优化，得到完全弛豫后的晶胞参数数据对比如表 1所示。

表 1(Table 1

表 1 不同相ZrO2的实验及优化前后晶胞参数 Table 1 Experimental and optimized parameters of polymorphs of ZrO2 晶相 晶格常数/Å 实验值/Å 分数坐标 晶胞体积/10-3 nm3 键长/Å 键布居值 m-ZrO2 a=5.233 6 b=5.268 4 c=5.418 4 Zr(0.275 9, 0.044 1, 0.210 2) O(0.061 0, 0.319 8, 0.354 6) O(0.452 9, 0.744 3, 0.978 0) 147.110 2.072, 2.101, 2.176， 2.190, 2.192, 2.267， 2.312 0.43, 0.32, 0.28， 0.22, 0.28, 0.26， 0.24 m-ZrO2a) a=5.197 9 b=5.236 2 c=5.394 8 5.15 5.21 5.32 Zr(0.275 1, 0.043 7, 0.210 5) O(0.062 5, 0.321 3, 0.345 6) O(0.452 2, 0.743 8, 0.973 5) 144.738 2.055, 2.082, 2.163， 2.165, 2.169, 2.278， 2.310 0.43, 0.32, 0.29， 0.27, 0.23, 0.25， 0.24 t-ZrO2 a=3.643 8 c=5.314 6 Zr(0.000 0, 0.000 0, 0.000 0) O(0.000 0, 0.500 0, 0.306 0) 141.127 2.093(4)b), 2.442(4)b) 0.67, 0.31 t-ZrO2a) a=3.618 3 c=5.283 1 3.60 5.18 Zr(0.000 0, 0.000 0, 0.000 0) O(0.000 0, 0.500 0, 0.308 0) 138.339 2.074(4)b), 2.433(4)b) 0.67, 0.30 c-ZrO2 a=5.149 9 Zr(0.000 0, 0.000 0, 0.000 0) O(0.250 0, 0.250 0, 0.250 0) 136.588 2.230(8)b) 1.00 c-ZrO2a) a=5.112 4 5.08 Zr(0.000 0, 0.000 0, 0.000 0) O(0.250 0, 0.250 0, 0.250 0) 133.625 2.214(8)b) 0.97 a—表示优化后; b—括号内数字表示相同键长的键的个数。

下载CSV 表 1 不同相ZrO2的实验及优化前后晶胞参数 Table 1 Experimental and optimized parameters of polymorphs of ZrO2

优化后的晶格常数与文献[11]中的实验值相比最大偏差均在2%以内，能够较好地吻合，从m相到t相再到c相的变化过程中，ZrO₂密度分别为5.65、6.10和6.27 g/cm³，即温度升高时，从m→t→c相变过程发生体积收缩，而冷却时，则发生体积膨胀，这与表 1中完全弛豫后的晶胞体积数据也相对应。

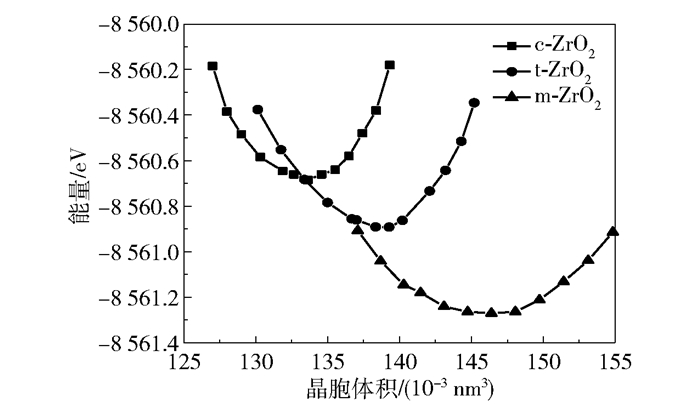
晶胞能量相对体积的变化可以反映材料的稳定性^[19]，计算并绘制出三相结构的能量、体积曲线如图 1所示。可以看出，在晶胞完全弛豫后m相具有能量最低点，说明在3种同质异性体结构中m相相对最为稳定，其抛物线底部最平缓且开口最大，说明m相有相对较好的稳定韧性；抛物线的整体平移说明不同晶相的能量(温度)不同导致相变同时伴有较大的体积效应。

图 1(Fig. 1)

图 1 不同晶相ZrO2体积与能量的关系 Fig.1 Volume-energy relationships of ZrO2 with different crystalline phases

从表 1中的键长及其成键布居值可以得出三相变化的具体机制。由硬球理论可知，若要形成稳定的八面体配位结构，晶体中的阳、阴离子半径比(r⁺/r^-)应大于0.732，当r⁺/r^- < 0.732，离子的配位数为8时，由于静电吸引力小、排斥力大而会使得体系变得不稳定^[20]。在CaF₂型结构的氧化锆中r⁺/r^-≈0.564，八配位结构会导致晶体内氧间隙太小，虽然氧八面体空隙只有4个被锆原子占据，但相邻氧原子之间的库仑排斥力会使结构变得不稳定(因数据量较大表 1中未详细列出)，所以低温下Zr⁴⁺倾向于形成配位数小于8的m相(7个配位键长分别为0.205 5、0.208 2、0.216 3、0.216 5、0.216 9、0.227 8、0.231 0 nm)，而均为Zr—O八配位结构的t、c相只能在高温下借助晶格振动平衡才稳定存在^[11]。具体变化是当m-ZrO₂发生第一级马氏体相变时，由于Zr原子在各方向上受到不同大小的作用力，氧原子的交叉层会沿该方向向上或向下轻微移动，顺着晶格振动方向，之前七配位的O阴离子中3个较短的Zr—O键作用力较强，加入1个氧原子与Zr原子一起形成了一个扁平四面体，而另外4个较长的Zr—O键顺着晶格振动方向在一定程度上远离Zr原子，形成了狭长的四面体，最终形成t-ZrO₂；若温度持续升高，晶格振动的加剧又会促使热膨胀产生，这时新增能量会弥补较低的Zr—O键能，当t相两类Zr—O键能逐渐接近于没有本质区别时，达到新的平衡态即形成c-ZrO₂。

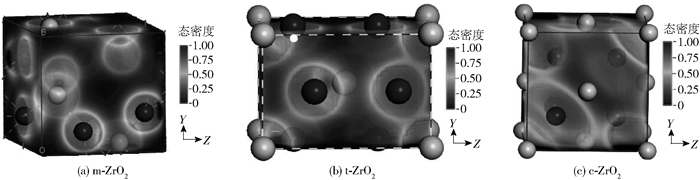
3种晶相分别使用GGA、GGA+U和hybrid B3LYP方法进行计算，所得能带带隙值汇总于表 2。采用传统密度泛函理论(local density approximation(LDA)或GGA)计算时由于忽略了高能级电子尤其是d、f电子之间的强关联作用，因此在计算过渡金属氧化物或氮化物时常会远远低估绝缘体或半导体的带隙^[15]，有时甚至会出现定性的错误，而GGA+U方法通过对选定原子设置U值，直接加入经验补偿项来弥补GGA方法的不足, 可以较好地应用于含有强关联体系的性质研究。有报道称GGA+U方法对某些体系如ZnO的带隙计算有较好的改善^[21]，但从我们对ZrO₂体系的计算结果来看，与实验结果^[22]相比，GGA、GGA+U方法得出的结果至少要比实验值低30%以上，说明对于本文体系GGA+U方法效果不明显。其原因主要还是DFT框架对交换项能量的经验近似处理不适合于Zr—O体系，而使用添加了20%的Hartree-Fock(HF)精确交换项作为交换相关泛函的B3LYP杂化泛函的计算结果与实验值能较好地吻合。这一点从能量计算的电荷差分密度分布图(图 2)中可以看出，在所研究的ZrO₂体系中，随着晶胞总能量的增加，氧原子外围白色的球面半径逐渐增大，电荷分布趋向于远离原子核中心，结合表 1中给出的键布居值分析，可以认为从m-ZrO₂到t-ZrO₂再到c-ZrO₂的转变过程中，电子之间的相互作用以Zr—O共价键的形态逐渐增强，电子趋向于集中到Zr—O原子中间位置使得电子间自相互作用增强，而对于这部分的能量计算，相对于添加了准确交换项的B3LYP方法，GGA和GGA+U近似方法的处理结果与实验结果不符。因此可以认为对于电子密度相对空间变化较大、交换关联能所占比重较大的体系，局域密度近似或梯度近似的半经验方法计算不如B3LYP方法准确。

表 2(Table 2

表 2 不同相ZrO2的禁带宽度的实验和计算值 Table 2 Experimental and calculated band-gaps of polymorphs of ZrO2 晶相 禁带宽度/eV 带隙类型 实验值 GGA GGA+U B3LYP m-ZrO2 5.83 3.668 3.844 5.767 间接 t-ZrO2 5.78 3.498 3.507 5.712 间接 c-ZrO2 6.10 3.313 3.327 5.853 间接

下载CSV 表 2 不同相ZrO2的禁带宽度的实验和计算值 Table 2 Experimental and calculated band-gaps of polymorphs of ZrO2

图 2(Fig. 2)

图 2 不同相电荷差分密度空间分布 Fig.2 Charge differential density distribution of different phases

需要说明的是，在一般温度和压力下，实验中很难获得纯t-ZrO₂和c-ZrO₂的晶体样品，文献[22]、[23]中使用不同比例Y₂O₃掺杂稳定后的晶体样品，采用真空紫外光谱法(vacuum ultraviolet, VUV)测量禁带宽度值，因此m-ZrO₂的禁带宽度的理论与实验结果吻合较好，t-ZrO₂和c-ZrO₂的理论与实验结果有差别，这与文献中所用的ZrO₂实验样品中掺杂了不同成分的Y₂O₃也有一定关系。

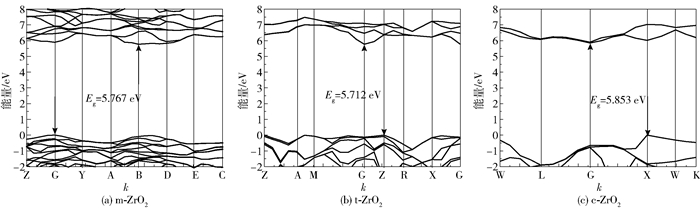
与表 2相对应，3种计算方法得出的带隙类型结果是一致的，ZrO₂带隙均为间接带隙，由于GGA、GGA+U方法计算结果与实验值相比偏差比较大，本文不展示其能带结构图。一般情况下基态深能级能带数据对材料的宏观性能影响较小，因此以费米能级为零点，取附近的能带数据，作出以B3LYP方法计算得出的3种晶相的能带结构图如图 3所示。可以看出，相对于t、c相，m相自由度多、键长不统一以及因结构复杂导致的费米面附近能带线条数最多且最密集。同时还可看出m相的能带线上下变化幅度比较平缓，说明m相比其他相的电子更加局域化，也相对更容易稳定。

图 3(Fig. 3)

图 3 不同相的能带结构 Fig.3 Band structure of different phases

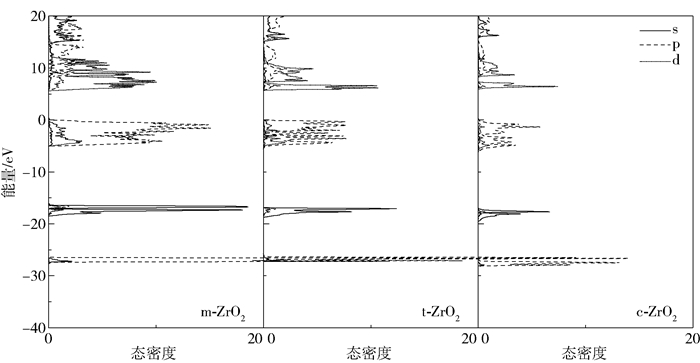
为得到更细致的电子间相互作用，绘制了不同晶相的总态密度和分波态密度图如图 4、5所示，同样只分析B3LYP杂化泛函计算出的结果。

图 4(Fig. 4)

图 4 不同晶相电荷总态密度 Fig.4 Total densities of state of electrons in different crystalline phases

图 5(Fig. 5)

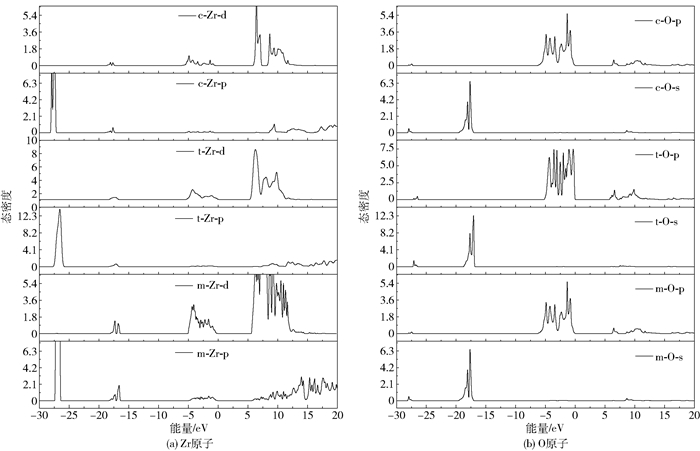
图 5 不同相ZrO2电子分波态密度 Fig.5 Partial densities of states of electrons in different ZrO2 phases

从总态密度图可以看出，不同晶相的价带主要有3部分构成。-27 eV附近的深能级价带主要由p电子构成，且从m相到c相逐渐减少，从分波态密度图上可以看出这里的p电子主要由Zr原子贡献；-18 eV处的价带主要由O的2s电子贡献，且从m相到c相其贡献也逐渐减少。

深能级价带对材料性能的影响较小，因此重点讨论费米面附近的价带。结合总、分态密度图对此价带顶和导带底进行详细分析，其中价带顶主要由O的2p电子贡献，O的2s电子的贡献几乎可以忽略，m、t、c相的顶层价带始末位置分别在-5.136~-0.007 eV、-5.323~-0.050 eV、-6.507~-0.162 eV处，价带顶位置逐渐下移。价带的移动方向取决于各原子态间成键或反键的相互作用，若p—d反键相互作用增强会使得价带向高能方向移动，反之则价带向低能方向移动；若d—d成键相互作用增强会使得价带向低能方向移动，反之则价带向高能方向移动^[21]。结合图 4易得，从m相到c相转化过程中，价带顶位置下移是由p—d成键相互作用增强引起的。随着平均近邻原子距离的减小^[23]，价带顶宽度(WUVB)分别为5.129、5.273、6.345 eV，可以看出其值逐渐增大，其中c相的WUVB计算值与实验值(6.50 eV)相当接近^[24]，与Králik等^[25]使用LDA方法计算的结果(5.2、5.4、6.1 eV)在变化方向上也趋于一致。

导带底主要由Zr的4d电子所贡献，O的2p电子有少量贡献，O的2s电子的贡献几乎可以忽略。m、t、c相的导带底始末位置分别为5.771~24.255 eV、5.815~7.278 eV、5.865~7.227 eV，导带底逐渐上移是由p—d成键相互作用增强引起的，导带底宽度(WLCB)分别为18.484、1.463、1.362 eV，其值逐渐减小。其中特别的是m相各层导带中间没有劈裂，这主要是由于O的2p电子能量的连续分布。而t相和c相导带劈裂逐渐明显，目前尚没有发现其他文献对此有所报道及解释，我们认为是由m相中O空位缺陷所致，而t相和c相的劈裂是由原子空间分布对称性增加引起的，同时说明了m-ZrO₂中O配位及Zr—O键长及键角分布的非对称性，这在荧光陶瓷材料领域有一定的研究价值^[26-28]。

(1) 运用密度泛函框架理论对常见的3种ZrO₂晶相的几何结构及电子结构进行了系统研究，采用广义梯度近似平面波GGA方法以及PBE交换关联函数对不同晶胞结构充分优化，得到与实验值接近的晶格参数，绘制了晶胞参数与总能量大小的关系曲线，据此比较并解释了三相之间的稳定性关系。

(2) 以优化后的晶胞为模型，分别使用GGA、GGA+U、B3LYP这3种方法对3种晶相模型进行计算，计算结果表明对于含d电子强关联体系的过渡金属氧化物ZrO₂，使用B3LYP杂化泛函计算出的3种带隙宽度的结果(5.767、5.712、5.853 eV)能与实验结果(5.78~6.10 eV)较好地匹配。

(3) 利用杂化泛函B3LYP计算出3种晶胞的电荷差分密度分布以及电子能总、分态密度，并根据这些数据分析解释了3种晶胞内化学键的构成及物性变化的内部机理，即从m相到c相的转变过程中，Zr—O原子之间的p—d共价键成分逐渐增强。