引言

表面波又叫作瑞利波, 这种波在弹性体表面传播, 只侵入弹性体内一小段距离, 当离弹性体表面很远时, 位移趋于零。表面波的发现对地震科学的发展起到了推动作用，不仅可以解释许多地球物理、声学和工程力学现象, 而且还具有实际意义, 例如应用于地震、石油、地质的勘探, 材料的无损探伤, 工程结构的抗震抗爆以及岩土动力学等领域。常见的关于表面波的研究有两种方法：一种是解析法, 即求解表面波在相应定解条件下的解，该方法大部分都是从直角坐标系出发, 导出经典的波动方程从而进行研究；另一种是数值方法, 利用有限元、边界元等手段对一些复杂结构中的表面波问题求近似解。Thomson^[1]最早提出求解固体介质中弹性波的矩阵方法, 之后被Haskell^[2]推广到表面波垂直分量的计算中。近年来, 针对表面波的研究主要集中在其传播及性质应用方面。如杨天春等^[3]采用水平层状介质模型, 利用传递矩阵方法推导表面波的质点位移表达式, 同时对曲线特征进行分析。柴华友等^[4]研究表面源激发的瑞利波的传播特性, 比较了激发模态与简正模态相速度的差异。阎守国等^[5]利用数值方法研究了半空间表面波的传播和衰减特性, 发现通过该特性可以提高表面波勘探的准确性并扩大其应用范围。本文应用解析法对表面波的解进行分析, 得到了表面波的一般解。此外, 还研究了表面波一般解的结构以及不同行波解波速之间的关系。

1 数学模型

弹性体内的表面波也是一种弹性波, 因此满足弹性力学基本方程组^[6]

$ (\lambda+G) \nabla(\operatorname{div} \boldsymbol{U})+G \Delta \boldsymbol{U}=\rho \frac{\partial^{2} \boldsymbol{U}}{\partial t^{2}} $

式中, U=(u, v, w)为位移矢量, u、v、w均为x、y、z和t的函数, ρ为弹性体的密度, $G = \frac{E}{{2\left( {1 + \nu } \right)}}$为剪切弹性模量, $\lambda = \frac{{\nu E}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}$为拉梅常数, E、ν分别为弹性模量和泊松比。

1.1 表面波的平面应变假设

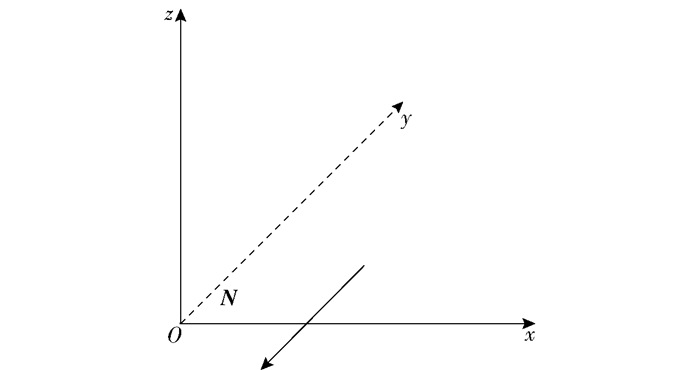
对本文所讨论的弹性体, 以y=0为弹性体表面, y轴指向弹性体内, 建立如图 1所示的坐标系。在平面应变假设下, 边界的法向量N=(0, -1, 0), 弹性体变形为二维的, 即U=(u(x, y, t), v(x, y, t), 0)。

由表面波的特性可知表面波满足

$ \lim \limits_{y \rightarrow+\infty} \boldsymbol{U}=\bf{0} $

(1)

弹性体表面为自由振动, 数学表示为

$ y=0:\left\{\begin{array}{l} u_{y}+v_{x}=0 \\ \lambda e+2 G v_{y}=0 \end{array}\right. $

(2)

式中，e为体积膨胀率。

自然边界条件为

$ (\mathrm{i}) \boldsymbol{U}=\boldsymbol{U}(x, y, t) 有界 $

(3)

$ (\mathrm{ii}) \forall 取定 x, y, \lim \limits_{t \rightarrow \pm \infty} \boldsymbol{U}=\bf{0} $

(4)

1.2 模型的求解方法

根据向量分析引理, 将弹性波分解为膨胀波和畸变波的叠加, 即U=U₁+U₂, 分别满足

$ \left\{\begin{array}{l}\frac{\partial^{2} \boldsymbol{U}_{1}}{\partial t^{2}}=\frac{2 G+\lambda}{\rho} \Delta_{2} \boldsymbol{U}_{1} \\ \operatorname{rot} \boldsymbol{U}_{1}=0\end{array}\right. $

(5)

和

$ \left\{\begin{array}{l} \frac{\partial^{2} \boldsymbol{U}_{2}}{\partial t^{2}}=\frac{G}{\rho} \Delta_{2} \boldsymbol{U}_{2} \\ \operatorname{div} \boldsymbol{U}_{2}=0 \end{array}\right. $

(6)

式中, U₁=(u₁, v₁, 0), U₂=(u₂, v₂, 0)分别表示膨胀波和畸变波的解, Δ₂=ə_x²+ə_y²为二维拉普拉斯算子。

2 模型的求解 2.1 膨胀波的解

运用分离变量法求解方程组(5)。为了运算方便, 将$\frac{{2G + \lambda }}{\rho }$记作a², 则式(5)变为

$ \left\{\begin{array}{l} \frac{\partial^{2} u_{1}}{\partial t^{2}}=a^{2} \Delta_{2} u_{1} \\ \frac{\partial^{2} v_{1}}{\partial t^{2}}=a^{2} \Delta_{2} v_{1} \\ \frac{\partial v_{1}}{\partial x}=\frac{\partial u_{1}}{\partial y} \end{array}\right. $

求解v₁, 令v₁=X₁(x)Y₁(y)T₁(t), 代入得X₁(x)Y₁(y)T″₁(t)=a²(X″₁(x)Y₁(y)T₁(t)+X₁(x)Y″₁(y)T₁(t))，两边同除X₁(x)Y₁(y)T₁(t), 得到

$ \frac{T_{1}^{\prime \prime}(t)}{T_{1}(t)}=a^{2}\left(\frac{X_{1}^{\prime \prime}(x)}{X_{1}(x)}+\frac{Y_{1}^{\prime \prime}(y)}{Y_{1}(y)}\right) $

(7)

若式(7)成立, 需满足$\frac{T_{1}^{\prime \prime}(t)}{T_{1}(t)}$、$\frac{X_{1}^{\prime \prime}(x)}{X_{1}(x)}$、$\frac{Y_{1}^{\prime \prime}(y)}{Y_{1}(y)}$分别是与t, x, y无关的常数，可分别设

$ p=\frac{T_{1}^{\prime \prime}(t)}{T_{1}(t)}, s=\frac{X_{1}^{\prime \prime}(x)}{X_{1}(x)}, r=\frac{Y_{1}^{\prime \prime}(y)}{Y_{1}(y)} $

先求解本征值问题T″₁(t)=pT₁(t)，步骤如下。

1)p>0, 通解为${T_1}(t) = {a_1}{{\rm{e}}^{\sqrt {pt} }} + {a_2}{{\rm{e}}^{ - \sqrt {pt} }}$。

当a₁≠0或a₂≠0时, $\mathop {\lim }\limits_{t \to {\rm{ \pm }}\infty } $T₁(t)=±∞, 这与自然边界条件(3)矛盾, 故该本征值问题无p>0的本征值。

2) p=0, 通解为T₁(t)=a₁+a₂t。

(ⅰ)当a₂=0时, T₁(t)=a₁, 由自然边界条件(4)可知a₁=0。

(ⅱ)当a₂≠0时, $\mathop {\lim }\limits_{t \to {\rm{ \pm }}\infty } $T₁(t)=±∞, 与自然边界条件(3)矛盾, 所以a₂=0。

综上, 该本征值问题没有p=0的本征值。

3) p < 0, 令p=-p₁², 通解为

$ T_{1}(t)=a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right) $

同理求解本征值问题X″₁(x)=sX₁(x), 令s=-s₁², 可得X₁(x)=d₁cos(s₁x)+d₂sin(s₁x)。

本征值问题Y″₁(y)=rY₁(y)的求解步骤如下。

1) r < 0, 通解为

$ Y_{1}(y)=c_{1} \cos (\sqrt{-r} y)+c_{2} \sin (\sqrt{-r} y) $

此时不满足条件(1), 所以r < 0不是该本征问题的本征值。

2) r=0, 通解为Y₁(y)=c₁+c₂y。

当c₁≠0或c₂≠0时, 不满足条件(1), 所以该本征值问题没有r=0的本征值。

3) r>0, 通解为${Y_1}(y) = {c_1}{{\rm{e}}^{\sqrt {ry} }} + {c_2}{{\rm{e}}^{ - \sqrt {ry} }}$。

由式(1)得c₁=0, 则Y₁(y)=${c_2}{{\rm{e}}^{ - \sqrt {ry} }}$, 令r=r₁², 得Y₁(y)=c₂e^-r₁y。

综上, X₁(x)、Y₁(y)和T₁(t)分别表示为

$ \left\{\begin{array}{l} X_{1}(x)=d_{1} \cos \left(s_{1} x\right)+d_{2} \sin \left(s_{1} x\right) \\ Y_{1}(y)=c_{2} \mathrm{e}^{-r_{1} y} \\ T_{1}(t)=a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right) \end{array}\right. $

(8)

式中a₁、a₂、c₂、d₁、d₂均为常数。

将式(8)代入v₁=X₁(x)Y₁(y)T₁(t), 得

$ \begin{array}{l} \ \ \ \ \ \ \ \ v_{1}=c_{2} \mathrm{e}^{-r_{1} y}\left(d_{1} \cos \left(s_{1} x\right)+d_{2} \sin \left(s_{1} x\right)\right)\left(a_{1} \cos \left(p_{1} t\right)+\right. \\ \left.a_{2} \sin \left(p_{1} t\right)\right) \end{array} $

由式(5)中第二个式子得$\frac{{\partial {u_1}}}{{\partial y}} = \frac{{\partial {v_1}}}{{\partial x}}$, 两边分别对y积分

$ \begin{array}{l} \ \ \ \ \ \ \ \ u_{1}=\frac{s_{1} c_{2}}{-r_{1}} \mathrm{e}^{-r_{1} y}\left(-d_{1} \sin \left(s_{1} x\right)+d_{2} \cos \left(s_{1} x\right)\right)\cdot \\ \left(a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right)\right)+C_{1}(x, t) \end{array} $

故u₁, v₁分别为

$ \left\{\begin{aligned} u_{1}=& \frac{s_{1} c_{2}}{-r_{1}} \mathrm{e}^{-r_{1} y}\left(-d_{1} \sin \left(s_{1} x\right)+d_{2} \cos \left(s_{1} x\right)\right)\cdot \\ &\left(a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right)\right)+C_{1}(x, t) \\ v_{1}=& c_{2} \mathrm{e}^{-r_{1} y}\left(d_{1} \cos \left(s_{1} x\right)+d_{2} \sin \left(s_{1} x\right)\right) \cdot \\ &\left(a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right)\right) \end{aligned}\right. $

(9)

式中C₁(x, t)是关于x, t的函数。

又由式(7)可得

$ r_{1}^{2}=s_{1}^{2}-\frac{p_{1}^{2}}{a^{2}}=s_{1}^{2}-h^{2} $

(10)

式中，${h^2} \buildrel \Delta \over = \frac{{{\rho _1}}}{{V_1^2}} = \frac{{\rho {p_1}}}{{\lambda + 2G}}$, r₁>0，这里V₁为膨胀波波速, 且有$V_1^2 = \frac{{\lambda + 2G}}{\rho } = \frac{{E(1 - \nu )}}{{(1 + \nu )(1 - 2\nu )\rho }}$。当式(9)中的参数满足式(10)的条件时, 就得到了膨胀波的解。

2.2 畸变波的解

与膨胀波的求解类似, 若令${d^2} = \frac{G}{\rho }$, 可得方程(6)的一般解为

$ \left\{\begin{aligned} u_{2}=& c_{2}^{\prime} \mathrm{e}^{-r_{2} y}\left(d_{1}^{\prime} \cos \left(s_{2} x\right)+d_{2}^{\prime} \sin \left(s_{2} x\right)\right) \cdot \\ &\left(a_{1}^{\prime} \cos \left(p_{2} t\right)+a_{2}^{\prime} \sin \left(p_{2} t\right)\right) \\ v_{2}=&-\frac{s_{2} c_{2}^{\prime}}{r_{2}} \mathrm{e}^{-r_{2} y}\left(d_{1}^{\prime} \sin \left(s_{2} x\right)-d_{2}^{\prime} \cos \left(s_{2} x\right)\right)\cdot \\ &\left(a_{1}^{\prime} \cos \left(p_{2} t\right)+a_{2}^{\prime} \sin \left(p_{2} t\right)\right)+C_{2}(x, t) \end{aligned}\right. $

(11)

式中C₂(x, t)是关于x、t的函数, 且有

$ r_{2}^{2}=s_{2}^{2}-\frac{p_{2}^{2}}{d^{2}}=s_{2}^{2}-k^{2} $

(12)

式中${{k^2} \buildrel \Delta \over = \frac{{p_2^2}}{{V_2^2}} = \frac{{\rho p_2^2}}{G}}$, r₂>0, 这里V₂为畸变波波速, 且${V_2^2 = \frac{G}{\rho } = \frac{E}{{2(1 + \nu )\rho }}}$。当式(11)中的参数满足式(12)时, 就得到了畸变波的解。

2.3 表面波的解

将式(9)、(11)这两个解叠加得

$ \left\{\begin{array}{l} u=\frac{s_{1} c_{2}}{-r_{1}} \mathrm{e}^{-r_{1} y} \varphi_{1}+c_{2}^{\prime} \mathrm{e}^{-r_{2} y} \varphi_{2}+C_{1}(x, t) \\ v=c_{2} \mathrm{e}^{-r_{1} y} \varphi_{3}-\frac{s_{2} c_{2}^{\prime}}{r_{2}} \mathrm{e}^{-r_{2} y} \varphi_{4}+C_{2}(x, t) \end{array}\right. $

(13)

式中φ₁、φ₂、φ₃和φ₄都是关于x, t的函数。

$ \left\{\begin{aligned} \varphi_{1}=&\left(-d_{1} \sin \left(s_{1} x\right)+d_{2} \cos \left(s_{1} x\right)\right) \cdot \\ &\left(a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right)\right) \\ \varphi_{2}=&\left(d_{1}^{\prime} \cos \left(s_{2} x\right)+d_{2}^{\prime} \sin \left(s_{2} x\right)\right) \cdot \\ &\left(a_{1}^{\prime} \cos \left(p_{2} t\right)+a_{2}^{\prime} \sin \left(p_{2} t\right)\right) \\ \varphi_{3}=&\left(d_{1} \cos \left(s_{1} x\right)+d_{2} \sin \left(s_{1} x\right)\right) \cdot \\ &\left(a_{1} \cos \left(p_{1} t\right)+a_{2} \sin \left(p_{1} t\right)\right) \\ \varphi_{4}=&\left(d_{1}^{\prime} \sin \left(s_{2} x\right)-d_{2}^{\prime} \cos \left(s_{2} x\right)\right) \cdot \\ &\left(a_{1}^{\prime} \cos \left(p_{2} t\right)+a_{2}^{\prime} \sin \left(p_{2} t\right)\right) \end{aligned}\right. $

由式(1)得

$ \lim \limits_{y \rightarrow+\infty} \boldsymbol{U}=\left(\begin{array}{c} C_{1}(x, t) \\ C_{2}(x, t) \\ 0 \end{array}\right)=\bf{0} $

所以C₁(x, t)=0, C₂(x, t)=0。

利用C₁=C₂=0, 则式(13)变为

$ \left\{\begin{array}{l} u=\frac{s_{1} c_{2}}{-r_{1}} \mathrm{e}^{-r_{1} y} \varphi_{1}+c_{2}^{\prime} \mathrm{e}^{-r_{2} y} \varphi_{2} \\ v=c_{2} \mathrm{e}^{-r_{1} y} \varphi_{3}-\frac{s_{2} c_{2}^{\prime}}{r_{2}} \mathrm{e}^{-r_{2} y} \varphi_{4} \end{array}\right. $

(14)

将式(14)代入式(2)中第一个式子, 可得当y=0时有

$ 2 s_{1} c_{2} \varphi_{1}(x, t)+\left(-r_{2} c_{2}^{\prime}-\frac{s_{2}^{2} c_{2}^{\prime}}{r_{2}}\right) \varphi_{2}(x, t)=0 $

(15)

下面证明s₁=s₂。由于系数c₂, c′₂, d_i, d′_i, a_i，a′_i具有任意性(i=1, 2), 不妨取c₂=c′₂=1, d₁=-d′₂=0，d₂=d′₁=1, a₁=a′₁=1, a₂=a′₂=0。

则式(15)变为

$ k_{1} \cos \left(s_{1} x\right) \cos \left(p_{1} t\right)+k_{2} \cos \left(s_{2} x\right) \cos \left(p_{2} t\right)=0 $

式中，k₁=2s₁, k₂=-r₂-$\frac{{s_2^2}}{{{r_2}}}$。令t=0可得

$ k_{1} \cos \left(s_{1} x\right)+k_{2} \cos \left(s_{2} x\right)=0 $

又k₁=2s₁≠0, 可得cos(s₁x)、cos(s₂x)线性相关, 由此有s₁=s₂。同理可得p₁=p₂。

利用s₁=s₂, 式(15)变为

$ 2 s_{1} c_{2} \varphi_{1}(x, t)+\left(-r_{2} c_{2}^{\prime}-\frac{s_{1}^{2} c_{2}^{\prime}}{r_{2}}\right) \varphi_{2}(x, t)=0 $

(16)

下面证明对任意的x, t都有φ₁(x, t)=φ₂(x, t)。

由系数的任意性, 不妨令

$ c_{2}=\frac{r_{2}^{2}+s_{1}^{2}}{2 s_{1} r_{2}} c_{2}^{\prime} $

代入式(16)得(r₂²+s₁²)(φ₁-φ₂)=0。又(r₂²+s₁²)>0, 所以有φ₁=φ₂。

将式(14)代入式(2)中第二个式子, 同理得φ₃=φ₄。

将φ₁=φ₂, φ₃=φ₄和s₁=s₂代入式(14)得

$ \left\{\begin{array}{l} u=\left(\frac{s_{1} c_{2}}{-r_{1}} \mathrm{e}^{-r_{1} y}+c_{2}^{\prime} \mathrm{e}^{-r_{2} y}\right) \varphi_{1} \\ v=\left(c_{2} \mathrm{e}^{-r_{1} y}-\frac{s_{1} c_{2}^{\prime}}{r_{2}} \mathrm{e}^{-r_{2} y}\right) \varphi_{3} \end{array}\right. $

(17)

将式(17)代入式(2)可得

$ \left\{\begin{array}{l} 2 r_{2} s_{1} c_{2}+c_{2}^{\prime}\left(-r_{2}^{2}-s_{1}^{2}\right)=0 \\ \lambda\left(s_{1}^{2} c_{2}-r_{1}^{2} c_{2}\right)+2 G\left(-r_{1}^{2} c_{2}+r_{1} s_{1} c_{2}^{\prime}\right)=0 \end{array}\right. $

(18)

求解式(18)即可得表面波的解。

3 解的性质 3.1 解的波速

虽然表面波的解不唯一, 但是其波速并不会随解的不同而发生改变, 下面证明这一性质。从一般解式(14)入手, 将式(14)代入式(2), 得到式(18)，发现与变量x、y、t有关的项全部被消除了, 只与常数r₁、r₂、s₁、c₂、c′₂有关, 因此不妨预测不同解的波速是相同的。

由式(18)得

$ \left\{\begin{array}{l} 2 r_{2} s_{1}+K\left(-r_{2}^{2}-s_{1}^{2}\right)=0 \\ \lambda\left(r_{1}^{2}-s_{1}^{2}\right)+2 G\left(r_{1}^{2}-K r_{1} s_{1}\right)=0 \end{array}\right. $

(19)

式中常数$K = \frac{{{{c'}_2}}}{{{c_2}}}$。利用式(19)中第二个式子和式(10)、(12), 以及

$ \frac{k^{2}}{h^{2}}=\frac{\lambda+2 G}{G}=2+\frac{\lambda}{G} $

可得

$ K=\frac{-k^{2}+2 s_{1}^{2}}{2 s_{1} \sqrt{s_{1}^{2}-h^{2}}} $

将K代入式(19)中第一个式子, 有

$ 4 s_{1}^{2} \sqrt{s_{1}^{2}-k^{2}} \sqrt{s_{1}^{2}-h^{2}}=\left(k^{2}-2 s_{1}^{2}\right)^{2} $

两边分别平方再同除s₁⁸, 得

$ 16\left(1-\frac{k^{2}}{s_{1}^{2}}\right)\left(1-\frac{h^{2}}{s_{1}^{2}}\right)=\left(\frac{k^{2}}{s_{1}^{2}}-2\right)^{4} $

(20)

又由式(10)、(12)可得膨胀波波速$V_1^2 = \frac{{p_1^2}}{{{h^2}}}$, 畸变波波速$V_2^2 = \frac{{p_1^2}}{{{k^2}}}$, 再由式(9)、(11)可得表面波的速度$V_3^2 = \frac{{p_1^2}}{{s_1^2}}$, 记$\alpha = \frac{{{V_3}}}{{{V_2}}}$, 又$\frac{{V_2^2}}{{V_1^2}} = \frac{{1 - 2\nu }}{{2(1 - \nu )}}$, 代入式(20)化简得

$ \alpha^{6}-8 \alpha^{4}+\frac{8(2-\nu)}{1-\nu} \alpha^{2}-\frac{8}{1-\nu}=0 $

(21)

式(21)的求解参考文献[1]。由式(21)可得α的值只与ν有关, 当ν取定时, α为定值。当ν=0.25时, 可得α=0.919 4, 则波速

$ V_{3}=\alpha V_{2}=0.919\;4 \sqrt{\frac{G}{\rho}} $

(22)

特别地, 当ν=0.5时, 可得α=0.955 3 < 1, 表面波波速V₃=αV₂=0.955 3$\sqrt{\frac{G}{\rho}}$ < V₂ < V₁。

由式(22)可知, α确定后, 表面波的波速只与剪切弹性模量G和弹性体的密度ρ有关。当这两个量固定时, 表面波所有行波解的波速是相等的, 并且与文献[1]所求右行波解的波速吻合。

同时, 还可以得到弹性体内膨胀波、畸变波和表面波的速度大小关系为V₃ < V₂ < V₁。

3.2 解的结构

由式(16)得到了表面波的一般解, 下面我们探索表面波的解的结构。令$a = \left( {\frac{{{s_1}{c_2}}}{{ - {r_1}}}{{\rm{e}}^{ - {r_1}y}} + } \right.\left. {c_2^\prime {{\rm{e}}^{ - {r_2}y}}} \right)$, $b = \left( {{c_2}{{\rm{e}}^{ - {r_1}y}} - \frac{{{s_1}c_2^\prime }}{r}{{\rm{e}}^{ - {r_2}y}}} \right)$，则式(17)变为

$ \left\{\begin{array}{l} u=u_{1}+u_{2}=a \varphi_{1} \\ v=v_{1}+v_{2}=b \varphi_{3} \end{array}\right. $

(23)

对式(23)利用积化和差公式, 得

$ \boldsymbol{U}=\left(\begin{array}{l} u \\ v \end{array}\right)=\left(\begin{array}{ll} a & 0 \\ 0 & b \end{array}\right)\left(l_{1} \boldsymbol{h}_{1}+l_{2} \boldsymbol{h}_{2}+l_{3} \boldsymbol{h}_{3}+l_{4} \boldsymbol{h}_{4}\right) $

式中l₁、l₂、l₃、l₄和h₁、h₂、h₃、h₄分别为

$ l_{1}=\frac{d_{2} a_{2}-d_{1} a_{1}}{2}, l_{2}=\frac{-d_{1} a_{1}-d_{2} a_{2}}{2} $

$ l_{3}=\frac{d_{1} a_{2}+d_{2} a_{1}}{2}, l_{4}=\frac{-d_{1} a_{2}+d_{2} a_{1}}{2} $

$ \boldsymbol{h}_{1}=\left(\begin{array}{c} \sin \left(s_{1} x+p_{1} t\right) \\ -\cos \left(s_{1} x+p_{1} t\right) \end{array}\right), \boldsymbol{h}_{2}=\left(\begin{array}{c} \sin \left(s_{1} x-p_{1} t\right) \\ -\cos \left(s_{1} x-p_{1} t\right) \end{array}\right) $

$ \boldsymbol{h}_{3}=\left(\begin{array}{c} \cos \left(s_{1} x+p_{1} t\right) \\ \sin \left(s_{1} x+p_{1} t\right) \end{array}\right), \boldsymbol{h}_{4}=\left(\begin{array}{c} \cos \left(s_{1} x-p_{1} t\right) \\ \sin \left(s_{1} x-p_{1} t\right) \end{array}\right) $

易证h₁, h₂, h₃, h₄线性无关。

事实上, 由k₁h₁+k₂h₂+k₃h₃+k₄h₄=0，通过取x, t分别为0, 联立解得k₁=k₂=k₃=k₄=0。

综上, 可得解的结构为

$ \boldsymbol{U}=\left(\begin{array}{l} u \\ v \end{array}\right)=\left[a^{\prime}\left(\begin{array}{cc} -\frac{s_{1}}{r_{1}} & 0 \\ 0 & 1 \end{array}\right)+b^{\prime}\left(\begin{array}{cc} 1 & 0 \\ 0 & -\frac{s_{1}}{r_{2}} \end{array}\right)\right] \boldsymbol{\xi} $

(24)

式中，ξ∈span{h₁, h₂, h₃, h₄}，a′∈span{e^-r₁y}, b′∈span{e^-r₂y}。

由此可知解有3种可能, 即左行波、右行波或者左右行波的叠加。特别地, 当l₂=1, l₁=l₃=l₄=0时, 得到了文献[1]所给的右行波解。

4 结论

本文基于弹性力学基本方程组和向量分析引理, 利用分离变量法, 分别得到了满足条件的膨胀波和畸变波的解, 通过叠加最终得到表面波的一般解。在对一般解的分析中得到的结论如下。

(1) 表面波的解不唯一。它的一般解的结构为

$ \boldsymbol{U}=\left(\begin{array}{l} u \\ v \end{array}\right)=\left[a^{\prime}\left(\begin{array}{cc} -\frac{s_{1}}{r_{1}} & 0 \\ 0 & 1 \end{array}\right)+b^{\prime}\left(\begin{array}{cc} 1 & 0 \\ 0 & -\frac{s_{1}}{r_{2}} \end{array}\right)\right] \boldsymbol{\xi} $

其中ξ∈span{h₁, h₂, h₃, h₄}，a′∈span{e^-r₁y}, b′∈span{e^-r₂y}。

这些行波解可能为左行波, 也可能为右行波, 还可能为左右行波的叠加。

(2) 当ν取定时, 表面波不同解的波速只与弹性体密度ρ和剪切弹性模量G有关。膨胀波、畸变波和表面波的速度大小关系为V₃ < V₂ < V₁。