自从覆膜电极发明以来,膜覆盖的克拉克(Clark)型溶解氧(DO)电极在诸多领域中得到了广泛的应用。利用膜覆盖电极测量溶解氧具有简单、快速、受水中其他溶质干扰少的优点,可对废水处理单元或电厂锅炉用水的溶解氧浓度进行连续实时监测。基于相同的检测原理,不同领域的溶解氧电极不断被开发出来,以满足实际应用的需要,例如,用于环保和养殖领域的DO电极、用于细胞组织氧测量的氧微电极、用于电厂锅炉给水和半导体工业中微量氧测量的DO电极等。溶解氧传感器的性能取决于氧电极的制造工艺、结构等多方面,应用于不同领域的氧电极在结构和性能上差异较大。然而应用于环境监测和电力领域的极谱式溶解氧测量电极的内置结构基本一致。Clark型溶解氧传感器作为一个电化学测量系统,主要由金属电极、电解液和硬件电路组成。要实现对溶解氧稳定而准确的测量,需要对传感器各部分进行合理设计和装配,在使电化学反应稳定进行的基础上实现对溶解氧浓度的测量。另外,氧气从待测液体到电极表面的扩散过程主要受透氧膜的控制,因此透氧膜的材质和厚度也很重要。
溶解氧传感器普遍存在电极寿命短、补偿精度不高、稳定性较差、使用和维护不便等问题。对溶解氧传感器的改进措施包括优化电极材料和结构、完善硬件电路、设计软件补偿等。张维维等[1]分析了极谱法溶解氧传感器输出稳定性的影响因素,并针对每种影响因素提出了相应的解决方法,提高了传感器输出的稳定性。张博森等[2]设计了一种高精度的极谱式溶解氧传感器检测电路,保证了溶解氧输出信号的准确性和稳定性。华国环等[3]通过在电流电压转换电路的精密电阻上并联一个储能电容,减少了极化时间,显著提高了溶解氧测定的响应速度。Xiao等[4]针对超声波自动清洁溶解氧传感器探头,提出了一种自动调节和适应温度变化的自动校准仪器的新方法,提高了传感器的使用寿命和测量精度。王莹[5]结合传感器的故障数据特征,利用卷积神经网络对溶解氧传感器的数据进行诊断,实现了对极谱式溶解氧传感器故障的有效识别。
虽然关于溶解氧传感器的研究已有较多报道, 但是多集中于硬件电路、软件补偿等方面,针对溶解氧电极结构的研究较少。本文在自制极谱式溶解氧传感器的基础上,根据阳极不同电极长度的实验测试结果,利用极限学习机(ELM)建立了电极长度与响应时间和输出电流之间关系的预测模型,利用得到的预测模型对传感器的电极反应面积进行寻优,找到使传感器在最佳状态下工作的阳极长度,并验证了传感器的测量稳定性和精度,为溶解氧传感器的设计提供了参考。
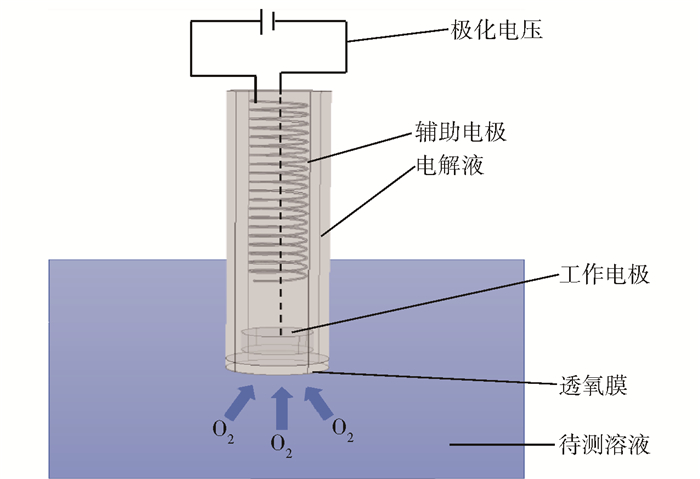
1 溶解氧传感器的检测原理覆膜溶解氧电极测量的基本原理可概括为:通过阴极覆盖薄膜控制氧的扩散;溶解氧电极的电流输出与液体介质中的氧活度或分压成正比。双电极Clark型溶解氧传感器通常使用金作为阴极,银作为阳极。当在电极两端施加极化电压E时,传感器开始工作,阴极表面上的氧分子获得电子并发生还原反应,而阳极上的银失去电子并发生氧化反应,完成电荷迁移过程,产生的扩散电流形成电流电路。将电解质与KCl和少量KOH混合得到电解质溶液,可以确保扩散到阴极表面上的氧分子与水分子结合形成OH-。双电极Clark型溶解氧传感器的结构如图 1所示,化学方程式如下。
阴极反应:
| $ {{\rm{O}}_2} + 2{{\rm{H}}_2}{\rm{O}} + 4{{\rm{e}}^ - } \to 4{\rm{O}}{{\rm{H}}^ - } $ | (1) |
阳极反应:
| $ 4{\rm{Ag}} + 4{\rm{C}}{{\rm{l}}^ - } \to 4{\rm{AgCl}} + 4{{\rm{e}}^ - } $ | (2) |
总体反应:
| $ {{\rm{O}}_2} + 2{{\rm{H}}_2}{\rm{O}} + 4{\rm{Ag}} + 4{\rm{C}}{{\rm{l}}^ - } \to 4{\rm{AgCl}} + 4{\rm{O}}{{\rm{H}}^ - } $ | (3) |
|
图 1 双电极Clark型溶解氧传感器的结构示意图 Fig.1 Schematic diagram of the structure of the two-electrode Clark type dissolved oxygen sensor |
氧浓度与氧还原电流之间的关系式为
| $ i = \frac{{nF{A_{\rm{S}}}D{C_{{\rm{DO}}}}}}{\delta } $ | (4) |
式中,i为扩散电流,n为参与反应的电子数,F为法拉第常数,AS为金阴极表面积,D为氧扩散系数,CDO为氧分子浓度,δ为透氧膜厚度。式(4)表明,在平衡条件下,产生的扩散电流与氧气浓度成正比。
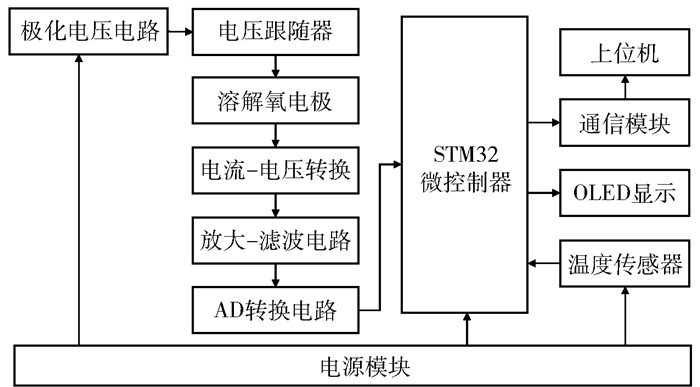
2 溶解氧传感器系统的构建与优化 2.1 溶解氧检测系统构建自制的溶解氧传感器电极采用STM32核心处理器,构建了由极化电路、电流-电压转换电路、放大滤波电路、温度采集模块等组成的硬件电路系统,硬件电路结构如图 2所示。开关电容电压转换器可为整个电路提供稳定的电源电压;电压调节电路和电压跟随器可为溶解氧传感器提供稳定的极化电压;电流转换电压电路可将溶解氧传感器检测到的微弱电流信号转换成电压信号,并通过电压放大滤波将电压信号放大;最后电极信号被传入STM32处理器进行记录并处理。温度传感器采用DS18B20单总线数字温度传感器,其具有抗干扰能力强、精度高的优点。
|
图 2 电路组成框图 Fig.2 Block diagram of circuit composition |
利用构建的系统,通过调整阳极银丝的长度来改变阳极接触面积。常温下将电极分别置于零氧水和饱和氧水中,测试传感器的残余电流、饱和电流和响应时间(包括上升和下降响应时间),结果如表 1所示。以传感器的响应时间、饱和电流、残余电流作为传感器的性能评价指标,通过建立回归模型寻找使传感器性能达到最优时所对应的阳极银丝长度,从而实现对传感器结构的优化,进而提高传感器的响应速度和测量精度。
| 下载CSV 表 1 不同阳极长度下溶解氧传感器的响应时间与输出电流 Table 1 Response time and output current of the dissolved oxygen sensor with different anode lengths |
采用极限学习机的方法,利用MATLAB对数据进行回归建模,以传感器的响应时间和输出电流作为输出变量,阳极银丝长度作为输入变量,构建基于极限学习机的1输入4输出模型,通过预测模型可以分析传感器的性能达到最佳状态时的阳极反应面积。极限学习机是Huang等[6]在2006年提出的针对单隐层前馈网络(SLFN)的新型快速学习算法,该算法随机选择隐藏节点并分析确定SLFN的输出权重,具有学习速度快、泛化能力好的特点[7]。此外,与支持向量机等方法相比,极限学习机在快速构建多输出模型方面也具有优势,可以快速构建多变量系统的预测模型[8]。
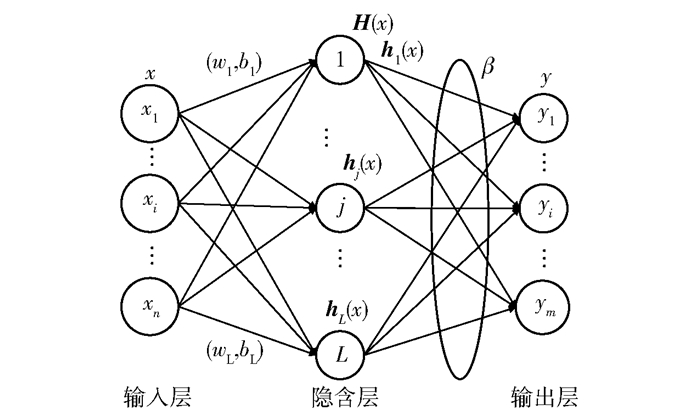
图 3为极限学习机的网络结构,训练样本集x作为神经网络的输入,中间为隐含层,输入层到隐含层通过全连接方式映射,隐含层输出H(x)的计算公式为
| $ \mathit{\boldsymbol{H}}(x) = \left[ {{h_1}(x), {h_2}(x), \cdots , {h_L}(x)} \right] $ | (5) |
|
图 3 极限学习机的网络结构 Fig.3 Network structure of the extreme learning machine |
对于任意N个样本(xi, yi),其中xi=[xi1, xi2, …, xin]T∈Rn,yi=[yi1, yi2, …, yim]T∈Rm,具有L个隐含节点和以g(x)为激活函数的单隐层前馈网络的建模过程如下[6]。
| $ {\sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\beta }}_i}} {g_i}\left( {{\mathit{\boldsymbol{x}}_j}} \right) = \sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\beta }}_i}} g\left( {{\mathit{\boldsymbol{w}}_i}{\mathit{\boldsymbol{x}}_j} + {b_i}} \right) = {\mathit{\boldsymbol{y}}_j}, j = 1, 2, \cdots , N} $ | (6) |
式中,wi=[wi1, wi2, …, win]T是连接第i个隐藏节点和输入节点的权重向量,βi=[βi1, βi2, …, βim]T是连接第i个隐藏节点和输出节点的权重向量,bi是第i个隐含节点的阈值。隐含层的输出是输入乘以对应权重之后加上偏差,再通过一个非线性函数对其所有节点结果求和得到。隐含层的输出H(x)是极限学习机的非线性映射(隐含层输出矩阵)。上述方程可以展开为
| $ \mathit{\boldsymbol{H\beta = Y}} $ | (7) |
式中,H(w1, …, wL, b1, …, bL, x1, …, xN)=
| $ \mathit{\boldsymbol{\beta }} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\beta }}_1^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{\beta }}_L^{\rm{T}}} \end{array}} \right]_{L \times m}}, \mathit{\boldsymbol{Y}} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}_1^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{y}}_L^{\rm{T}}} \end{array}} \right]_{N \times m}} $ | (8) |
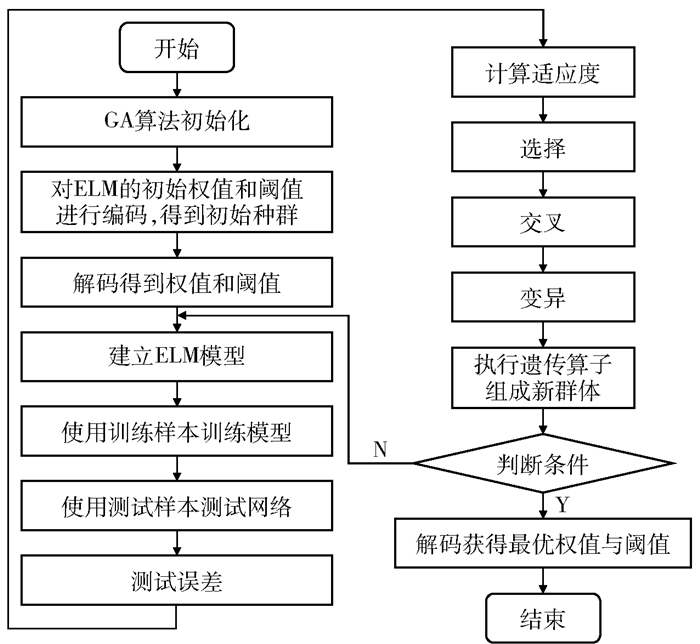
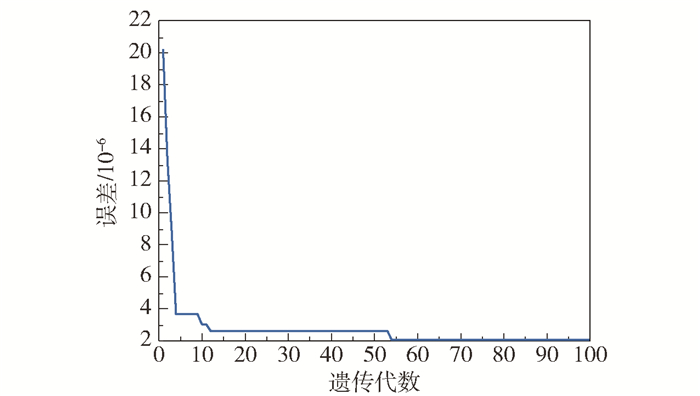
Hβ=Y的最小范数最小二乘解是唯一的,即β=H†Y。通过对单隐层神经网络进行训练,得到wi、bi、和βi使模型的输出与期望输出的误差达到最小。ELM的权值和阈值是随机初始化的,且隐含层神经元的节点数量过低会降低预测精度,过高则会产生过拟合现象。本文设置隐含层神经元节点的数量为8,采用遗传算法(GA)训练和优化ELM输入权值和隐含层阈值,得到最优的输入权值和隐含层阈值用于建立ELM预测模型。遗传算法是一种模拟生物种群遗传变异的自适应搜索算法,根据适者生存的自然法则,将问题转化为生物种群进化的过程,根据概率自适应改变搜索方向,以较快的速度求得最优解[9]。针对构建的GA优化的ELM模型,设定GA优化算法中种群数目为20,交叉及变异概率分别为0.7和0.01,最大遗传代数和代沟分别为100和0.95,适应度函数FitnV=(obj),运用GA对ELM的输入权值和隐含层阈值进行优化,算法流程图和进化过程分别如图 4和图 5所示。
|
图 4 GA-ELM算法流程图 Fig.4 Flow chart of the GA-ELM algorithm |
|
图 5 进化过程 Fig.5 Evolutionary process |
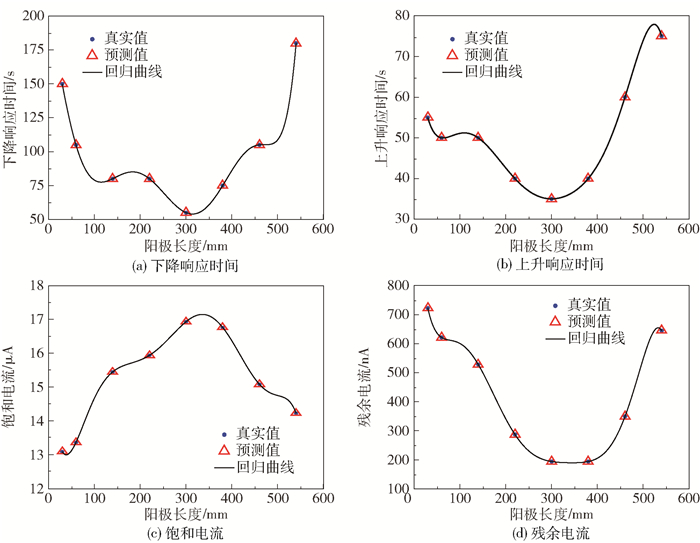
利用遗传算法优化极限学习机构建预测模型,传感器各项性能指标的回归曲线如图 6所示。从图 6中可以看出,预测值与真实值接近,回归曲线的拟合程度较好。由于数据集样本较少,采用同样的样本数据对训练模型进行测试,结果显示,使用随机权值和阈值测试样本的仿真误差为1.394×10-5,使用优化后的权值和阈值测试样本的仿真误差为2.668×10-6,模型的精度得到了有效提高。
|
图 6 溶解氧传感器各项性能指标的回归曲线 Fig.6 Regression curves of various performance indicators of the dissolved oxygen sensor |
采用平均绝对误差(MAE)和均方根误差(RMSE)来评估传感器各个指标的预测精度,经过遗传算法优化的预测模型和未经优化的模型精度如表 2所示,结果表明,优化后的模型精度高于未经优化的模型精度。因此,与极限学习机建立的预测模型相比,遗传算法优化极限学习机建立的模型精度得到了有效提高。
| 下载CSV 表 2 GA-ELM和ELM模型的精度比较 Table 2 Accuracy comparison between GA-ELM and ELM models |
利用建立的回归模型进行参数寻优,首先将传感器性能指标的回归输出进行归一化处理,将响应时间和输出电流归一化到0~1之间,并对饱和电流进行处理,用1减去归一化后的饱和电流值。将处理后的数据进行加和,作为回归模型寻优的目标函数。当目标函数值取最小值时,溶解氧传感器的响应时间最短,饱和氧时传感器的输出电流最大,零氧时输出电流最小,传感器的输出性能达到最佳状态。优化结果显示,当阳极银丝长度为322 mm时,即传感器的阳极和阴极接触面积之比约为33时,传感器的综合性能达到最佳状态,此时传感器的下降响应时间为54.3 s,上升响应时间为35.4 s,饱和电流为17.1 μA,残余电流为190.8 nA。结果表明,与未经优化的电极相比,优化的传感器的残余电流明显降低,响应速度得到有效提高。
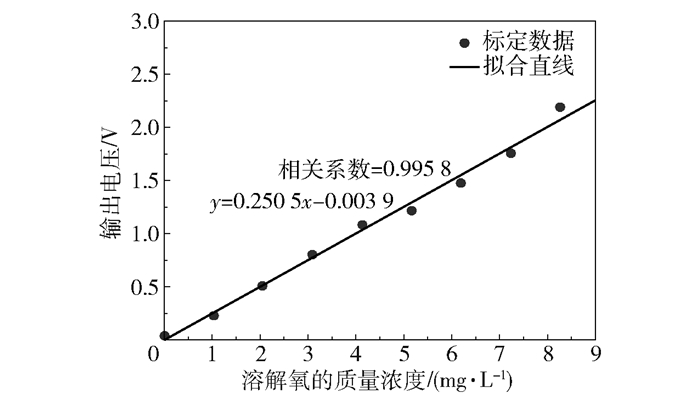
3 溶解氧传感器的标定与补偿设计 3.1 溶解氧传感器的标定电化学法测量溶解氧可以测量传感器的输出电流,通过线性计算得到溶解氧浓度。由于电极设计和制造水平等因素的差异,传感器的输出电流也不相同,因此测量前需要进行标定。使用多点标定方法对自制溶解氧传感器进行标定,得到的标定曲线如图 7所示,拟合的直线方程为:y=0.250 5x-0.003 9,相关系数为0.995 8,其中,x为溶解氧的质量浓度,y为传感器的输出电压。
|
图 7 溶解氧传感器的标定曲线 Fig.7 Calibration curve of the dissolved oxygen sensor |
在不同的温度条件下,水中氧的溶解度相差较大[10-11]。测量时的温度不同于校准时的温度,故需要对传感器的读数进行温度校正。根据GB11913—89[12],溶解氧饱和度Cs与温度T的关系可以通过回归方程得到:Cs=14.603 07-0.402 146 9×T+0.007 687 03×T2-0.000 069 257 5×T3。
由于溶解氧饱和度与温度之间的关系不是线性的,因此校准曲线在不同的温度下具有不同的斜率。当温度一定时,两点校准可以确定电流与溶解氧浓度的线性斜率KT,并建立温度T下传感器输出电压与溶解氧的映射关系。在溶解氧浓度的测定中,必须要充分考虑到温度对于传感器输出的影响。为提高溶解氧传感器的测量精度,需要对温度造成的影响进行补偿[13-14]。根据传感器在不同温度下的电流输出,建立溶解氧的质量浓度与传感器输出电压的线性关系,对不同温度下的线性斜率进行拟合,得到线性斜率KT随温度T变化的拟合方程为:KT= -1.824 6×10-7×T3+1.819 3×10-5×T2-7.552 2× 10-4×T+1.495 5×10-2。
4 实验验证 4.1 测量稳定性与残余电流导致输出电流变化的原因有极化电位偏移、电解质泄漏和浓度变化以及电解液存在气泡等因素。另外,还有两个重要的原因是工作电极表面发生钝化以及透氧膜与工作电极之间距离的变化。在自制的传感器中,选用了稳定性较高的金电极,保证了传感器在较长时间内工作的稳定性。
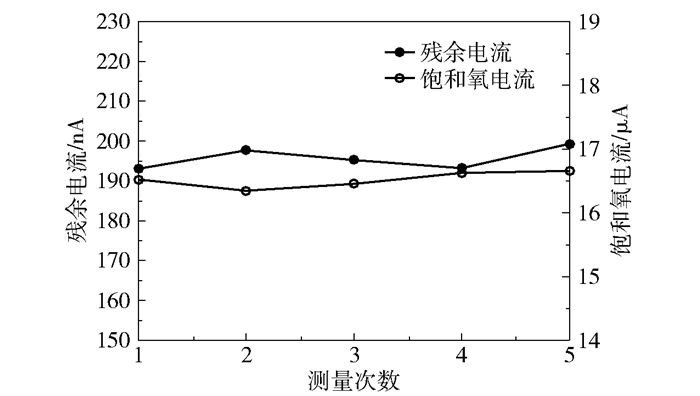
通常在氧浓度为零时,溶解氧传感器中几乎都存在残余电流。在25 ℃下对自制传感器的残余电流和稳定性进行了测试,结果如图 8所示,从图中可以看出,零氧状态下的残余电流小于0.2 μA,相当于约0.1 mg/L O2,而饱和溶解氧状态下的输出电流约为16.6 μA。在零氧和饱和氧状态下重复测定5次的输出电流变化较小,表明传感器具有较好的测量稳定性。
|
图 8 测量稳定性与残余电流 Fig.8 Measurement stability and residual current |
利用构建的传感系统对溶解氧含量进行测量,最低检测限可达到0.01 mg/L,将测量结果与HK-258型便携式溶解氧分析仪(北京华科仪科技有限公司)的测量值进行比较,结果如表 3所示。可以看出,传感器的相对误差小于1%,表明自制传感器具有较高的测量精度。
| 下载CSV 表 3 自制溶解氧传感器与商用传感器的测量结果比较 Table 3 Comparison of measurement results between the self-made dissolved oxygen sensor and a commercial sensor |
(1) 通过极限学习机建立阴阳极接触面积与传感器性能指标之间的预测模型并进行优化,结果表明,经过优化的电极具有更低的残余电流和更快的响应速度。
(2) 利用传感器零氧和饱和氧状态下的输出建立溶解氧浓度与传感器输出电压的线性关系,通过对不同温度下的线性斜率进行拟合,进而对温度参数进行补偿。经实验验证,自制传感器具有较好的测量稳定性和较高的测量精度。
| [1] |
张维维, 孙延玉. 极谱法溶解氧传感器输出稳定性研究[J]. 传感器与微系统, 2017, 36(4): 39-41. ZHANG W W, SUN Y Y. Research on stability of polarographic dissolved oxygen sensor[J]. Transducer and Microsystem Technologies, 2017, 36(4): 39-41. (in Chinese) |
| [2] |
张博森, 张函嘉, 李姗珊. 极谱式溶解氧传感器高精度检测电路设计[J]. 电子测量技术, 2019, 42(18): 163-167, 171. ZHANG B S, ZHANG H J, LI S S. Design of high precision polarographic dissolved oxygen sensor detection circuit[J]. Electronic Measurement Technology, 2019, 42(18): 163-167, 171. (in Chinese) |
| [3] |
华国环, 季泽峥, 刘清惓. 一种提高溶解氧测定响应速度的方法[J]. 传感技术学报, 2016, 29(11): 1655-1658. HUA G H, JI Z Z, LIU Q Q. A method to improve the response speed of the measurement of dissolved oxygen[J]. Chinese Journal of Sensors and Actuators, 2016, 29(11): 1655-1658. (in Chinese) |
| [4] |
XIAO Z, WANG J T, YI C, et al. The dissolved oxygen sensor design based on ultrasonic self-adaption and self-cleaning[J]. Complexity, 2020, 36: 1-8. |
| [5] |
王莹. 基于深度学习的极谱式溶解氧传感器故障诊断分析[D]. 泰安: 山东农业大学, 2020. WANG Y. Fault diagnosis analysis of polarographic dissolved oxygen sensor based on deep learning[D]. Taian: Shandong Agricultural University, 2020. (in Chinese) |
| [6] |
HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70: 489-501. DOI:10.1016/j.neucom.2005.12.126 |
| [7] |
冯禹铭, 董秀成, 金滔. 基于PSO-ELM的机器人精度补偿方法研究[J]. 计算机应用研究, 2019, 36(10): 3000-3003. FENG Y M, DONG X C, JIN T. Research on methods of robot accuracy compensation based on PSO-ELM[J]. Application Research of Computers, 2019, 36(10): 3000-3003. (in Chinese) |
| [8] |
王晶, 靳其兵, 曹柳林. 面向多输入输出系统的支持向量机回归[J]. 清华大学学报(自然科学版), 2007, 47(S2): 1737-1741. WANG J, JIN Q B, CAO L L. Support vector regression algorithm for multi-input multi-output systems[J]. Journal of Tsinghua University (Science and Technology), 2007, 47(S2): 1737-1741. (in Chinese) |
| [9] |
陈则王, 李福胜, 林娅, 等. 基于GA-ELM的锂离子电池RUL间接预测方法[J]. 计量学报, 2020, 41(6): 735-742. CHEN Z W, LI F S, LIN Y, et al. Indirect prediction method of RUL for lithium-ion battery based on GA-ELM[J]. Acta Metrologica Sinica, 2020, 41(6): 735-742. (in Chinese) |
| [10] |
秦宏鹏, 刘翔宇, 陈娟. 溶解氧多参数智能补偿校正检测技术的研究[J]. 北京化工大学学报(自然科学版), 2019, 46(3): 99-104. QIN H P, LIU X Y, CHEN J. Multi-parameter intelligent compensation correction detection technology for determination of dissolved oxygen[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2019, 46(3): 99-104. (in Chinese) |
| [11] |
李文, 张志永, 金旭, 等. 基于ADuCM360多因素补偿的溶解氧传感器[J]. 仪表技术与传感器, 2020(1): 23-27, 31. LI W, ZHANG Z Y, JIN X, et al. Dissolved oxygen sensor based on ADuCM360 multi-factor compensation[J]. Instrument Technique and Sensor, 2020(1): 23-27, 31. (in Chinese) |
| [12] |
中华人民共和国国家环境保护局. 水质溶解氧的测定电化学探头法: GB11913-89[S]. 北京: 中国标准出版社, 1989. National Environmental Protection Agency of the People's Republic of China. Determination of dissolved oxygen in water by electrochemical probe method: GB11913-89[S]. Beijing: Standard Press of China, 1989. (in Chinese) |
| [13] |
张广辉, 邵惠鹤. 溶氧传感器的温度特性研究及其补偿[J]. 传感技术学报, 2006, 19(2): 323-327. ZHANG G H, SHAO H H. Temperature dependence and compensation for the dissolved oxygen probe[J]. Chinese Journal of Sensors and Actuators, 2006, 19(2): 323-327. (in Chinese) |
| [14] |
舒迪, 邱发强, 祁欣. 数字式微量溶解氧分析仪的研究[J]. 电子测量技术, 2010, 33(11): 14-17, 20. SHU D, QIU F Q, QI X. Study of trace amount of digital dissolved oxygen analytical instrument[J]. Electronic Measurement Technology, 2010, 33(11): 14-17, 20. (in Chinese) |








