随着现代化工过程愈加精密化、复杂化，其安全问题也逐渐受到重视。与其他工业过程故障相比，化工故障易引发毒气泄漏、爆炸等更大的危险事故^[1]，因此，适用于现代复杂化工过程的故障诊断方法引起广泛的关注并得到不断的发展。近年来，该领域的故障诊断技术已形成了一个庞大的体系^[2-5]，但由于化工过程的精确数学模型难以建立、专家经验的可移植性差等原因，基于解析模型和经验知识的方法的发展受到了极大限制；基于数据驱动的方法只需分析化工过程的历史数据即可进行有效的故障诊断，因而逐渐成为该领域的研究重点。主成分分析(PCA)、核主成分分析(KPCA)、独立成分分析(ICA)、Fisher判别分析(FDA)等多元统计方法^[6-9]，以及BP神经网络(BPNN)、支持向量机(SVM)等^[10-11]人工智能领域的浅层故障诊断方法均已在故障诊断领域取得了重要应用。此外, 多元统计方法与BP神经网络、支持向量机相结合的故障诊断研究也取得了重要成果^[12-14]。然而，这些故障诊断方法在处理高纬度、非线性、强耦合且具有时间序列信息的现代化工过程数据时，往往无法有效提取其特征，且无法分辨特征相似的故障类别，不能满足现代化工故障诊断的要求。

自编码器(auto-encoder, AE)作为一种无监督学习算法，已在现代化工故障诊断领域展现出比多元统计方法和浅层学习方法更好的诊断性能。冯倩玉^[15]提出一种基于降噪正交自编码器(denoising orthogonal auto-encoder, DQAE)的故障诊断算法，在自编码器基础上引入正交性和降噪处理，取得了较好的诊断效果，并在所提方法基础上进一步完善，解决了多故障同时发生的问题。Zheng等^[16]提出了一种基于堆栈自编码器(stacked auto-encoder, SAE)的故障诊断模型，结合t分布随机邻域嵌入(t-distributed stochastic neighbor embedding, t-SNE)算法和density-based spatial clustering of applications with noise(DBSCAN)聚类，在田纳西-伊斯曼(Tennessee-Eastman, TE)过程中实现了无监督故障诊断。张祥等^[17]提出了一种基于VAE-DBN(variational auto-encoder, VAE; deep belief network, DBN)的故障诊断方法，针对高维数据故障特征难以提取的问题，将变分自编码器与深度置信网络相结合，在TE过程实验中展现出了较好的诊断性能。此外，基于其他深度学习技术的故障诊断方法也在不断发展，如基于深度置信网络及其派生网络^[18-20]、基于卷积神经网络(convolutional neural network, CNN)及其派生网络^[21-24]，以及基于深度残差网络(deep residual network, DRN)的模型在化工故障诊断领域的应用^[25]等。然而上述方法在处理现代化工过程数据时，忽略了数据中的长时间依赖关系，提取到的故障特征不具备时间序列信息，整体故障诊断性能仍有待进一步提升。

长短期记忆(long short-term memory, LSTM)网络是一种适用于时间序列数据的深度学习模型，最早由Hochreiter等^[26]提出。LSTM借助特殊的“门”结构，解决了传统循环神经网络(recurrent neural network, RNN)的长期依赖问题，在语音识别、语言翻译等领域都取得了巨大成功。近年来，LSTM在机械故障诊断领域也取得了一定的研究成果，如Yuan等^[27]将LSTM用于航空发动机的剩余寿命预测，Lu等^[28]将LSTM用于滚动轴承的早期故障预测，王路瑶等^[29]将LSTM用于空调系统传感器故障的检测与诊断。在化工故障诊断领域，LSTM的应用研究则相对较少。Zhao等^[30]将LSTM用于连续数据的故障诊断，并在TE实验中验证了该方法的有效性，然而该方法所用的vanilla LSTM相对于其他LSTM变体的效果并不好，且实验结果易受随机噪声的影响，故障诊断性能仍有待提升。

本文提出了一种基于长短期记忆网络与降噪自编码器结合的LSTM-DAE化工故障诊断方法，针对传统DAE模型无法提取时间序列信息的缺点，引入LSTM对模型结构进行优化，并在TE过程仿真实验中验证了所提方法的有效性和优越性。

传统的基于DAE的故障诊断模型以3层的全连接层为特征提取网络，其输出节点数与输入节点数保持一致，均为原始数据的维度；隐层激活函数采用线性函数，以保证特征表示不被限制；以均方误差为损失函数，并以最小化重构误差为目标，用梯度下降算法进行训练。训练之前在原始数据中加入高斯噪声，这样可以迫使模型学习原始数据的特征表示，增强模型的鲁棒性。训练完成后，提取隐层输出即为特征。

学习特征提取步骤完成后，提取DAE模型的编码网络，在隐层节点后加上3层的Softmax分类器，利用神经网络全连接层强大的非线性处理性能来学习故障分类。Softmax分类器的输入节点数为特征的维度，输出节点数为故障类别数；隐层采用Sigmoid激活函数，输出层采用Softmax函数，选择交叉熵损失函数并采用梯度下降法训练。训练完成后得到的DAE模型虽然能够克服随机噪声的影响，并对原始数据进行有效的特征提取，但是由于其特征提取网络为浅层模型，特征学习能力受到限制。此外，DAE模型的全连接层结构决定了它无法提取原始数据中的时间序列信息。

为了提高模型的特征学习能力，并挖掘原始数据中的时间序列信息，引入LSTM对DAE模型进行改进，LSTM中“遗忘门”、“输入门”、“输出门”3种门结构以特殊的方式进行交互，构成了其独特的网络结构，如图 1所示, 其中，x_t-1、x_t、x_t+1表示LSTM的输入，h_t-1、h_t、h_t+1表示LSTM的输出；σ和tanh分别表示Sigmoid激活函数和tanh激活函数；×表示向量之间按元素相乘，+表示向量之间按元素相加。

图 1(Fig. 1)

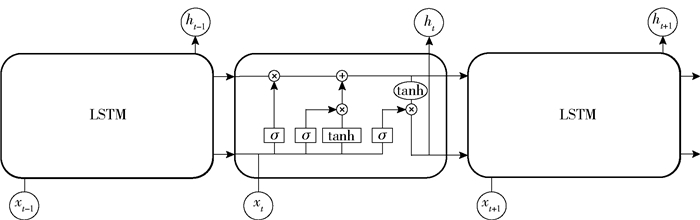
图 1 LSTM的结构 Fig.1 Structure of LSTM

改进后模型的网络结构如图 2所示，原始DAE模型的全连接层编码网络被替换为LSTM-DAE编码层。LSTM-DAE编码网络的输入节点数为原始数据的维度，其隐含层数为重要的超参数，需经过验证集寻优；在LSTM-DAE编码网络后，加上由两个全连接层组成的解码网络，其输出节点数与编码网络的输入节点数保持一致，输出的激活函数采用Sigmoid函数。

图 2(Fig. 2)

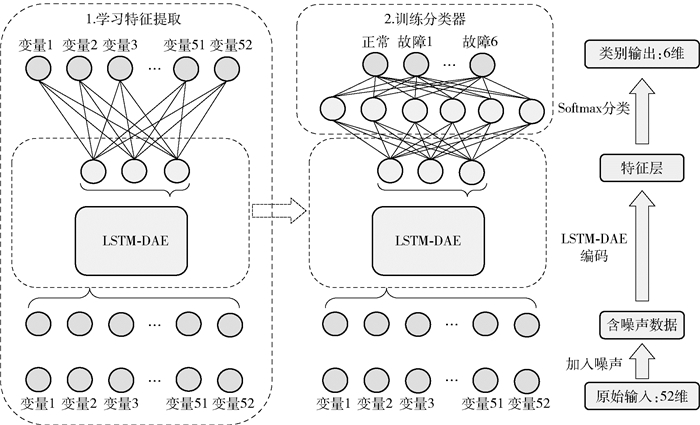
图 2 基于LSTM-DAE的故障诊断模型 Fig.2 FD model based on LSTM-DAE

以最小化重构误差为目标，用梯度下降法训练，训练完成后提取LSTM-DAE编码网络的隐层输出即为原始数据的特征。此时得到的特征，不仅由于DAE的强鲁棒性而不容易受到随机噪声的影响，而且得益于LSTM特有的网络结构能在时间维度上存储原始数据的时间序列信息，比改进前的DAE模型提取到的特征更准确、全面。

学习特征提取步骤完成后，提取LSTM-DAE编码的网络部分，在隐层节点后加上新的Softmax分类器并训练，最终得到基于LSTM-DAE的化工故障诊断模型，该模型由LSTM-DAE特征提取和Softmax分类器这两部分组成。完整的故障诊断流程如图 3所示。

图 3(Fig. 3)

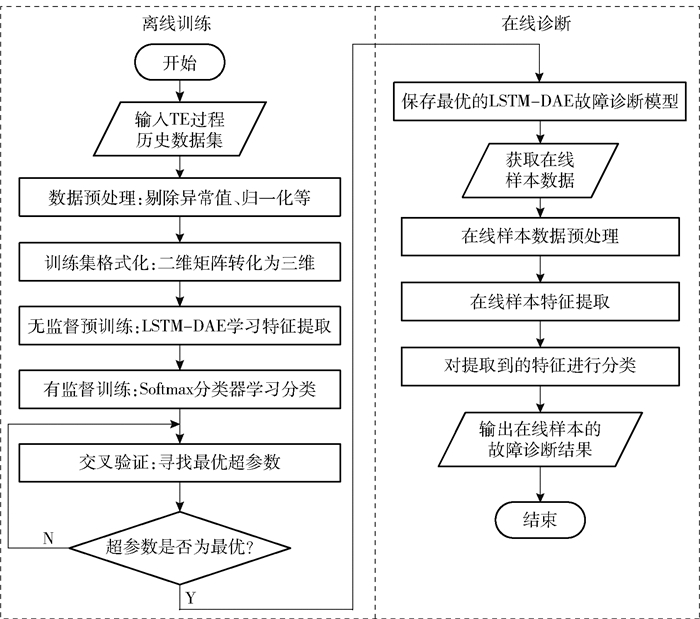
图 3 LSTM-DAE模型的故障诊断流程 Fig.3 FD process of the LSTM-DAE model

TE过程是美国田纳西州伊斯曼化学品公司对实际化工过程进行的计算机模拟，被普遍用于过程控制、监控和诊断方法的评价。TE过程包括52个观测变量、21种故障类型，样本采集间隔为0.05 h。训练集正常样本在25 h运行仿真下获得，观测数据总数为500，故障样本在24 h运行仿真下获得，观测数据总数为480；测试集数据在48 h运行仿真下获得，在第8小时时引入故障，因此观测数据的前160个为正常样本，后800个为故障样本。

为分析所提模型的多故障和单故障诊断性能，选择故障1、2、6、14、18共5类故障组成所需数据集。为了使测试集的实验结果能够准确描述模型的泛化能力，测试集不参与模型的调优过程，因此将原始训练集按照7∶3的比例重新划分，得到新的训练集和验证集。最终的训练集为2 030×52矩阵(2 030个样本，每个样本均为52维向量)，验证集为870×52矩阵，测试集为5 760×52矩阵。

以正确率(accuracy)指标来评价模型的多故障诊断效果，记作A，其定义为

式中，N_c为正确分类的样本数，N_t为样本总数。

对于单故障评价指标，考虑到TE过程中存在的数据偏斜问题^[31]，引入误报率R_FA(false alarm rate, FAR)、漏检率R_MD(miss detection rate, MDR)两个指标，定义如下。

式中，FP为假阳性数，TN为真阴性数，FN为假阴性数，TP为真阳性数，它们的定义如表 1中的混淆矩阵所示。

表 1(Table 1

表 1 单故障诊断的混淆矩阵 Table 1 Confusion matrix of single fault diagnosis 实际类别 定义 预测类别为1 预测类别为0 1 TP FP 0 FN TN 0表示正常样本，1表示故障样本。

下载CSV 表 1 单故障诊断的混淆矩阵 Table 1 Confusion matrix of single fault diagnosis

最后，在单故障评价问题中，引入故障检出点来表示模型实际检测到的故障发生的时间点，其确定方法为，在仿真实验引入故障后(即从第160个样本点开始)，模型首次将样本判别为故障的时间点，即为本次模拟的故障检出点。

本文提出的LSTM-DAE模型的可调参数很多，其中LSTM-DAE编码网络的隐含层数、隐层节点数是两个重要的超参数，对模型的正确率、平均误报率、平均漏检率，以及模型整体运行时间的影响很大。

由于LSTM特殊的网络结构，LSTM-DAE编码网络的隐含层数的选择受批训练大小的限制。在可选范围内选择2、4、5、10、20这5个值作为隐含层数的待选值。对每个取值重复10次平均实验，得到训练集平均正确率、测试集平均正确率以及平均总运行时间随隐含层数的变化关系，如图 4所示。

图 4(Fig. 4)

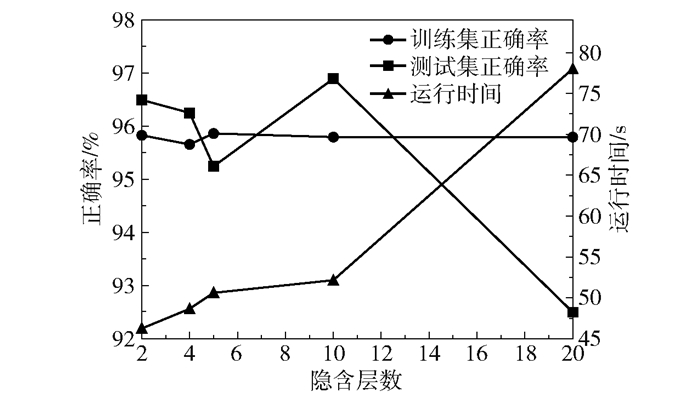
图 4 正确率和运行时间随隐含层数的变化关系 Fig.4 Variation in accuracy and running time as a function of the number of hidden layers

由图 4可知，随着隐含层数的增加，总运行时间增加，训练集正确率变化幅度不大，测试集正确率整体呈现出先升高再降低的趋势。表明随着模型结构的逐渐复杂，时间成本逐渐增加，模型的故障诊断效果不断提升。但过于复杂的模型结构不仅会使时间成本过高，而且反而会降低模型的故障诊断性能。因此，综合考虑时间成本和诊断性能, 选择10作为隐含层数的最优取值。

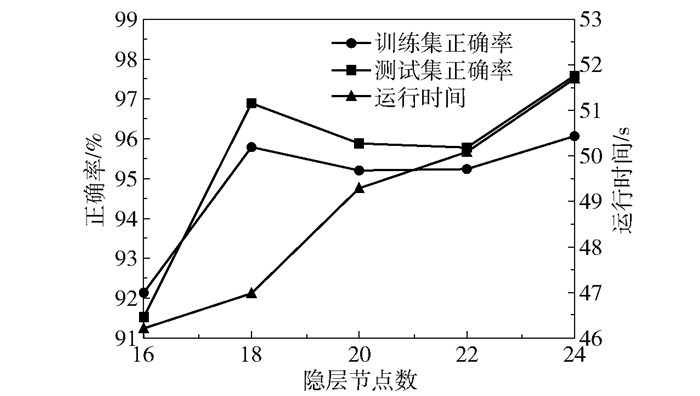
采用同样的实验方法来确定LSTM-DAE编码网络隐层节点数的取值。训练集平均正确率、测试集平均正确率以及平均总运行时间随隐层节点数的变化关系如图 5所示。

图 5(Fig. 5)

图 5 正确率和运行时间随隐层节点数的变化关系 Fig.5 Variation in accuracy and running time as a function of the number of hidden nodes

由图 5可知，随着隐层节点数的增加，运行时间增加，训练集、测试集正确率均呈现出先升再降再升的趋势。当隐层节点数大于22时，尽管正确率较高，但由于模型结构过于复杂，时间成本剧增，因此在对各个因素权衡考虑后，选择18作为隐层节点数的最优取值。

LSTM-DAE模型的其他超参数如批训练大小、迭代次数、学习率等的寻优结果如表 2所示。在最优超参数取值下，模型的训练集正确率为96.02%，测试集正确率为97.31%，总运行时间为48.366 s。

表 2(Table 2

表 2 LSTM-DAE模型的超参数 Table 2 Hyper-parameters of LSTM-DAE model   超参数 符号表示 LSTM-DAE 特征提取部分 Softmax 分类器部分 隐含层数 time_step 10 隐层节点数 hidden_num 18 40 学习率 α 0.012 0.01 正则化参数 lambda 0 0 Dropout参数 dropout_keep_prob 1.0 1.0 迭代次数 epochs 1 000 1 000 批训练大小 batch_size 256 256 噪声系数 decay_rate 0.3 学习率衰减率 μ 0.8 学习率衰减步数 decay_steps 100

下载CSV 表 2 LSTM-DAE模型的超参数 Table 2 Hyper-parameters of LSTM-DAE model

为了验证所提LSTM-DAE模型中深层编码网络的有效性，引入BP神经网络(含1个隐层)、支持向量机两个浅层故障诊断模型进行对比分析；为验证LSTM-DAE模型相对于多元统计模型的优越性，引入PCA、KPCA两个故障诊断模型作对比分析；为验证LSTM-DAE模型引入LSTM后的改进效果，将其与原始DAE模型作对比分析。

对所研究的6类模型均进行5次重复实验，实验结果如图 6所示，记录5次实验的平均值如表 3所示。由表 3可知，LSTM-DAE模型的训练集正确率高达96.02%，测试集正确率高达97.31%，平均误报率仅为0.65%，平均漏检率仅为3.19%。由图 6可知LSTM-DAE模型5次实验的正确率不仅最高，而且变化幅度很小，结果更为稳定，表明LSTM-DAE模型不易受随机噪声影响，具有很强的鲁棒性。

图 6(Fig. 6)

图 6 6类模型的正确率变化曲线 Fig.6 Variation in accuracy for the six models

表 3(Table 3

表 3 6类模型的各项评价指标 Table 3 Evaluation indicators of the six models 模型 训练集 正确率/% 测试集 正确率/% 平均误报 率/% 平均漏检 率/% BP 68.94 65.53 21.80 11.33 SVM 99.38 63.59 4.32 42.29 PCA 97.49 86.32 3.26 16.24 KPCA 97.85 90.34 3.77 9.76 DAE 93.40 95.54 1.31 7.88 LSTM-DAE 96.02 97.31 0.65 3.19

下载CSV 表 3 6类模型的各项评价指标 Table 3 Evaluation indicators of the six models

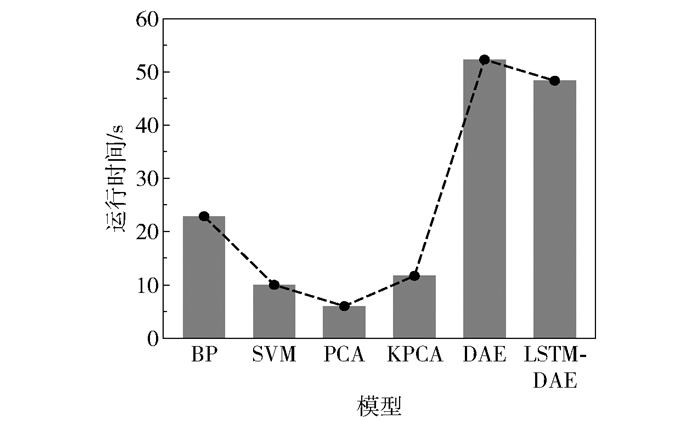
由图 7可知，所提的LSTM-DAE模型与原始DAE模型的总运行时间较其他4类模型的运行时间更长，这一方面是因为二者的模型结构更复杂，另一方面是它们的训练过程存在多次迭代过程，而PCA和KPCA模型均无此迭代过程。此外，相对于改进前的DAE模型，所提LSTM-DAE模型的总运行时间更短，且故障诊断效果更好，表明了所提方法的优越性。

图 7(Fig. 7)

图 7 6类模型的运行时间对比 Fig.7 Comparison of the running times of the six models

通过观察单故障实时监测图(图 8)，发现与原始DAE模型(改进前)相比，所提出的LSTM-DAE模型(改进后)对故障14、故障18的诊断具有较好的改善效果，因此对其改善的原因作进一步分析。

图 8(Fig. 8)

图 8 改进前后的故障实时监测图 Fig.8 Real-time monitoring curves of the models before and after improvement

图 8(a)所示为故障14的实时监测图，可以看出DAE模型在引入故障14后仍会将大量故障样本误判为正常样本，而LSTM-DAE模型在引入故障14后几乎没有误判的情况。由表 4可知，LSTM-DAE模型将故障14的漏检率从14.85%降至1.38%，而改进前后的故障检出点却仅仅相差2个样本点。以上结果表明：在故障14上，LSTM-DAE模型并没有明显缩短故障的检测时间，而是在故障发生后提高了对故障的辨别能力，大大减少了误判的情况，从而改善了对故障14的诊断效果。

表 4(Table 4

表 4 改进前后模型的单故障诊断效果对比 Table 4 Single fault diagnostic effects before and after improvement 模型 故障检 出点a) 漏检 率a)/% 故障检 出点b) 漏检 率b)/% DAE模型(改进前) 162 14.85 265 16.90 LSTM-DAE模型(改进后) 164 1.38 183 11.55 a—故障14；b—故障18。

下载CSV 表 4 改进前后模型的单故障诊断效果对比 Table 4 Single fault diagnostic effects before and after improvement

图 8(b)所示为故障18的实时监测图。LSTM-DAE模型的故障检出点显然比DAE模型更靠前。由表 4可知，改进前后两者的故障检出点相差82个样本点，即缩短了246 min的检测时间，从而使故障18的漏检率从16.90%降低至11.55%。以上结果表明：在故障18上，LSTM-DAE模型有效缩短了故障的检测延迟时间，从而改善了对故障18的诊断效果。

经过以上分析可知，LSTM-DAE模型不仅在多故障诊断效果上取得了比其他5类模型更高的正确率，而且在单故障诊断效果上也能够获得更低的漏检率，表明了所提方法的有效性和优越性。

(1) 提出了基于LSTM-DAE的化工故障诊断方法，用基于LSTM的特殊编码方式代替了传统DAE模型的全连接网络编码方式，并结合高斯噪声处理和全连接网络解码层，搭建出基于LSTM-DAE的特征提取模型，最后由Softmax分类器输出故障诊断结果。所提模型不仅具备DAE模型的强鲁棒性，而且由于引入了LSTM，使之能够挖掘数据中的时间序列信息，保证了编码特征获取的有效性。

(2) 在多故障诊断效果上，所提LSTM-DAE模型的训练集正确率达到了96.02%，测试集正确率达到了97.31%，平均误报率仅为0.65%，平均漏检率仅为3.19%，整体诊断效果优于BP神经网络、SVM、PCA、KPCA、DAE这5类故障诊断模型。

(3) 在单故障诊断效果上，LSTM-DAE模型提高了对故障14的辨别能力，缩短了对故障18的检测延迟时间，获得了比DAE模型更好的故障诊断效果。

所提LSTM-DAE模型不仅能够快速、准确地诊断故障，而且具有鲁棒性好、泛化能力强等优点。然而随着深度学习技术的不断发展，随之而来的问题也不断增加，如深度学习模型的网络结构愈加复杂，造成模型的超参数越来越多，超参数的调节也更加困难。如何结合智能优化算法(如遗传算法、蚁群算法) 对超参数自动寻优，都是今后具有重要研究意义的方向。