近年来，甲烷作为一种清洁燃料越来越被人们所重视，而采用金属有机框架材料(MOFs)实现甲烷的吸附^[1-3]和储存也引起了较为广泛的关注。随着实验室制备的MOFs以及计算机虚拟合成的MOFs的数量呈现爆发式的增长，仅仅利用巨正则系综蒙特卡洛模拟(GCMC)方法^[4-5]实现高性能吸附材料的高通量计算筛选已经无法满足要求。

基于GCMC的高通量筛选方法往往受限于庞大的MOFs数据库和有限的计算资源，因此，具有强大数据分析和挖掘能力的机器学习方法被研究者们用来进行高效的MOFs高通量筛选研究^[6-8]。基于此，本文采用机器学习建模的方法，通过决策树(DT)模型及其衍生的随机森林(RF)模型、极端随机树(ET)模型和梯度提升树(GBDT)模型这4种模型对吸附甲烷的MOFs材料进行高通量的计算筛选以选择出最佳性能材料；对两种较优模型(RF模型和GBDT模型)的参数优化进行了探究，并推荐了合适的材料结构特征参数。

目前，MOFs数据库基本上可划分为两类，即由实验合成的MOFs(eMOFs)所组成的数据库和由计算机合成的MOFs(hMOFs)所组成的数据库。尽管通过计算机合成的hMOFs为MOFs的种类提供了无限的可能，但是hMOFs数据库中的材料仅有一小部分能够在实验中合成，绝大部分hMOFs设计的合理性和可行性存在着很大问题，导致无法通过实验合成相应的材料。

本文采用eMOFs数据库^[9-10]，实验数据集中包含1 800个真实的MOFs数据样本，其中每一种MOFs由9种特征描述符来表征，即表 1中的前6种结构描述符和后3种化学信息描述符。通过GCMC模拟计算每种材料在温度298 K和压力35 bar (1 bar=0.1 MPa)下的甲烷吸附量，根据美国能源局对吸附甲烷的金属有机框架材料在该条件下的划分标准，将吸附量高于180(单位气体吸附量与单位材料的体积比)的数据样本标记为高性能材料，反之，则标记为低性能材料。

表 1(Table 1

表 1 每种材料特征向量的描述符表示 Table 1 Descriptors used to construct a feature vector for each material 特征向量 描述符 孔体积/(cm3·g-1) Pv 密度/(g·cm-3) Ds 比表面积/(cm2·g-1) Sa 限制孔径/Å PLD 最大孔径/Å MPD 主导孔径/Å DPD 电负性比率 Er 金属占比(原子数分数)/% Mp 不饱和度 Du

下载CSV 表 1 每种材料特征向量的描述符表示 Table 1 Descriptors used to construct a feature vector for each material

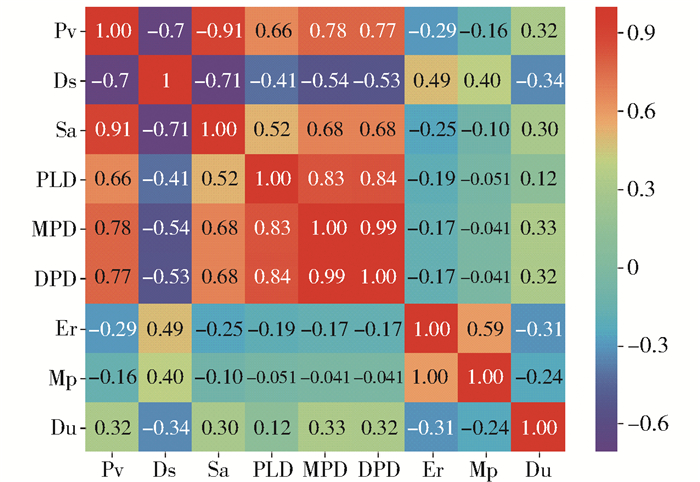
本文计算了每个描述特征之间的相关性，如图 1所示。

图 1(Fig. 1)

图 1 特征向量的相关性 Fig.1 Correlation of feature vectors

从图 1可以看出，材料的最大孔径(MPD)和主导孔径(DPD)的相关性非常强，达到了99%。由此可见，绝大多数材料的最大孔径和主导孔径是一致的。其次，可以看出每种材料的孔体积(Pv)和比表面积(Sa)的相关性也比较强，达到91%，实际上，当材料的孔径较大时，其相应的比表面积也会增大，以支撑MOFs的有机骨架结构，从而更好地实现对甲烷的吸附。与此同时，对于化学信息描述特征来说，它们之间的相关性都不高，而且与结构描述特征的相关性也不强。鉴于两者是从不同的角度对材料信息的提取，因此应该结合结构特征与化学信息特征共同完成材料的筛选。

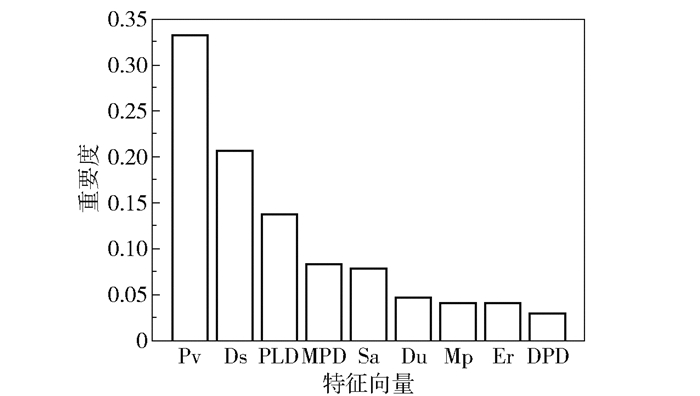
基于构造决策树时分裂节点的原理^[11]，进一步计算每个特征描述符对甲烷吸附能力的重要度。在每棵树的节点分裂时需要选择该节点的分裂特征，通过计算基尼系数来确定节点特征，基尼系数越小，划分的纯度越高，则节点特征越好，特征的重要度就越高。树的节点特征的顺序就是重要度的顺序。从图 2可以看出，MOFs材料的孔体积(Pv)对材料的吸附能力的重要度最高，这是因为材料的孔体积增大，甲烷的吸附量也会相应增加。除此之外，结构特征描述符对甲烷吸附的重要度较高，影响较大，而由于甲烷是非极性分子，材料的化学信息描述符对于甲烷吸附的重要度较小。因此，结构特征对于甲烷吸附材料性能的影响更大。

图 2(Fig. 2)

图 2 特征向量对甲烷吸附的重要度 Fig.2 Importance of feature vectors for methane adsorption

数据库中的很多材料由于结构原因导致某些特征无法测量，存在有缺省值问题，此外当按照分类标准划分时，存在高、低性能材料数量不平衡的问题，极有可能造成数学模型的不稳定。相比于其他机器学习的算法，由单棵决策树衍生出的多棵决策树是采用集成的学习方法，利用该方法建立模型对数据的要求相对较低，输出的结果更加可靠。为了比较不同机器学习算法的筛选能力，本文选择了决策树基础模型，及由它改进而来的随机森林、极端随机树和梯度提升树3种树模型，随机地将数据集划分为训练集和测试集两组，采用普遍的7:3的划分方式，即训练集和测试集的材料数分别为1 260种和540种。利用不同的机器学习方法对训练集进行学习，并使用建立的模型对测试集的数据进行筛选预测。

通过模型对材料的测试集进行筛选，计算各个模型的混淆矩阵^[12-13]。从表 2中各模型混淆矩阵的计算结果可以看出其分类效果，例如，GBDT模型在低性能材料的分类结果中，有375种材料分类正确，21种材料分类错误；而在高性能材料的分类结果中，有135种材料分类正确，9种材料分类错误。比较4个模型的混淆矩阵，发现它们的错误分类数量大小顺序为DT>ET>RF>GBDT，GBDT模型的误分个数明显低于其他模型。

表 2(Table 2

表 2 4种模型的混淆矩阵 Table 2 Confusion matrix for four models 模型 分类正确 数量a) 分类错误 数量a) 分类正确 数量b) 分类错误 数量b) 混淆矩阵 DT 382 37 91 30 382 30 37 91 ET 390 37 85 28 390 28 37 85 RF 390 36 91 23 390 23 36 91 GBDT 375 21 135 9 375 9 21 135 a—低性能样本；b—高性能样本。

下载CSV 表 2 4种模型的混淆矩阵 Table 2 Confusion matrix for four models

图 3给出了各个模型的ROC曲线，该曲线可以用来衡量模型的拟合程度^[14]。由图 3可以看出，随着误诊率的增加，召回率也逐渐增加。召回率T与误诊率F的计算公式如式(1)、(2)所示。

图 3(Fig. 3)

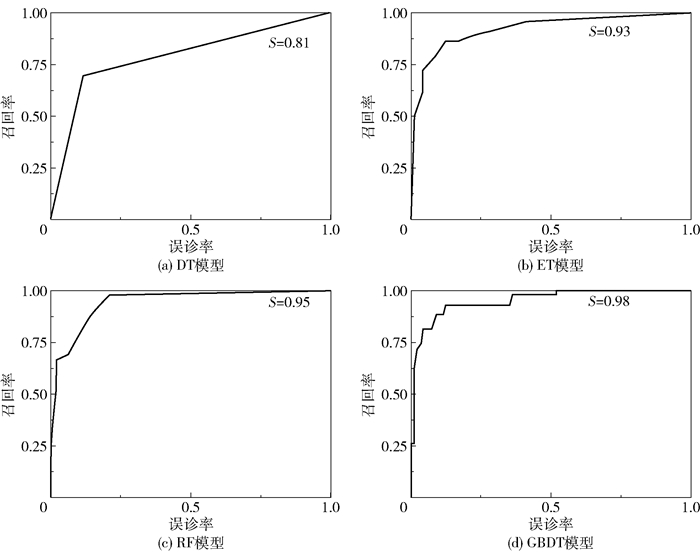
图 3 4种模型的ROC曲线 Fig.3 ROC curves of four models

式中，TP表示样本的真实类别是正例，并且模型将其预测成为正例的数量；FN表示样本的真实类别是负例，并且模型将其预测成为负例的数量；TN表示样本的真实类别是正例，模型将其预测成为负例的数量；FP表示样本的真实类别是负例，模型将其预测成为正例的数量。对于每一个模型，我们希望其有一个较高的召回率以及较低的误诊率，所以图 3中每一个图形的拐点越接近左上方则模型的效果越好，也即曲线与横坐标轴围成的面积越大越好。DT、ET、RF以及GBDT这4个模型曲线与横坐标轴所围成的面积分别为0.81、0.93、0.95和0.98。从面积上看，GBDT模型曲线的拐点更加靠近左上方，所围成的面积最大，表明GBDT模型比其他模型的拟合效果更好。

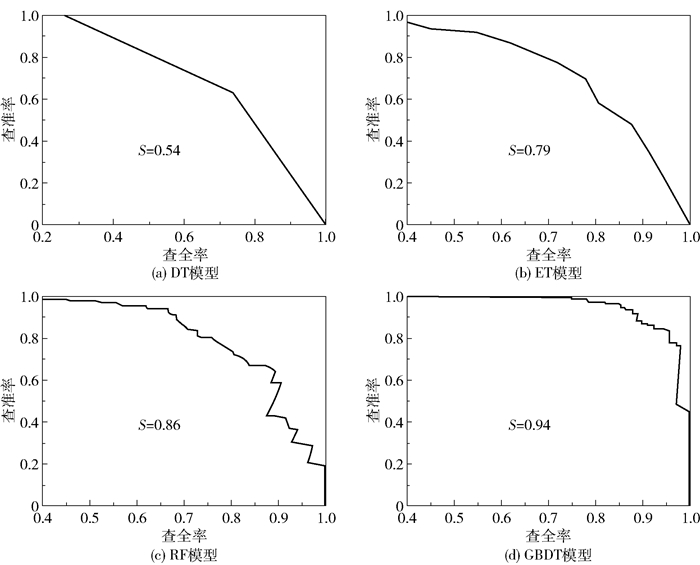
由于材料数据库中低性能的材料较多，高性能的材料较少，这种较差的样本均衡性会对模型的筛选造成一定的影响。因此，可以通过PR曲线来反映样本均衡性对模型的影响^[15]。4种模型的查准率-查全率曲线如图 4所示，查全率R以及查准率P的计算公式如(3)、(4)所示。

图 4(Fig. 4)

图 4 4种模型的PR曲线 Fig.4 PR curves of four models

可以看出，随着查全率的不断增加，查准率则在不断下降。对于一个较好的模型而言，应该有较高的查全率及查准率，即PR曲线的拐点尽量靠近右上方，使曲线与横坐标轴及左边框围成的面积越大越好。4种模型的PR曲线所围成的面积大小顺序为DT < ET < RF < GBDT，表明GBDT模型优于其他模型。对于GBDT模型，其PR曲线所围面积为0.94，仅仅比其ROC曲线所围面积减少了0.04，而RF模型的相应减少值为0.09，其他两个模型的减少值也都较大。因此可以表明，GBDT模型受数据集的样本不平衡的影响较小，模型稳定性较高。

基于DT、RF、ET和GBDT这4种机器学习模型对540种材料构成的测试集进行高性能甲烷吸附材料的筛选。从表 3可以看出，利用4种机器学习模型筛选的类别为0的低性能材料，其各项指标普遍比筛选出的类别为1的高性能材料要高，原因在于在训练集中进行高低性能的分类时，低性能材料的数量远多于高性能材料的数量，导致4种模型对于高性能材料的学习不充分，故而针对高性能材料筛选的效果不明显。4种模型筛选的准确度大小顺序为DT < ET < RF < GBDT。可见，相比于由单棵决策树组成的DT模型，由DT模型衍生出的多棵决策树组成的其他3种模型的分类效果更明显。而在由决策树衍生的分类模型中，GBDT的准确度达到0.96，筛选效果要好于ET和RF模型。

表 3(Table 3

表 3 4种模型测试集的比较 Table 3 Comparison of four models with test set 模型 类别 P T F1分数a) 准确度b) DT 0 0.90 0.86 0.88 0.82 1 0.61 0.70 0.65 RF 0 0.95 0.91 0.93 0.90 1 0.76 0.84 0.79 ET 0 0.94 0.94 0.93 0.88 1 0.68 0.81 0.74 GBDT 0 0.97 0.98 0.98 0.96 1 0.94 0.93 0.93 a—$\frac{2}{{{F_1}}} = \frac{1}{P} + \frac{1}{T}$；b—$A = \frac{{TP + TN}}{{TP + TN + FP + FN}}$。

下载CSV 表 3 4种模型测试集的比较 Table 3 Comparison of four models with test set

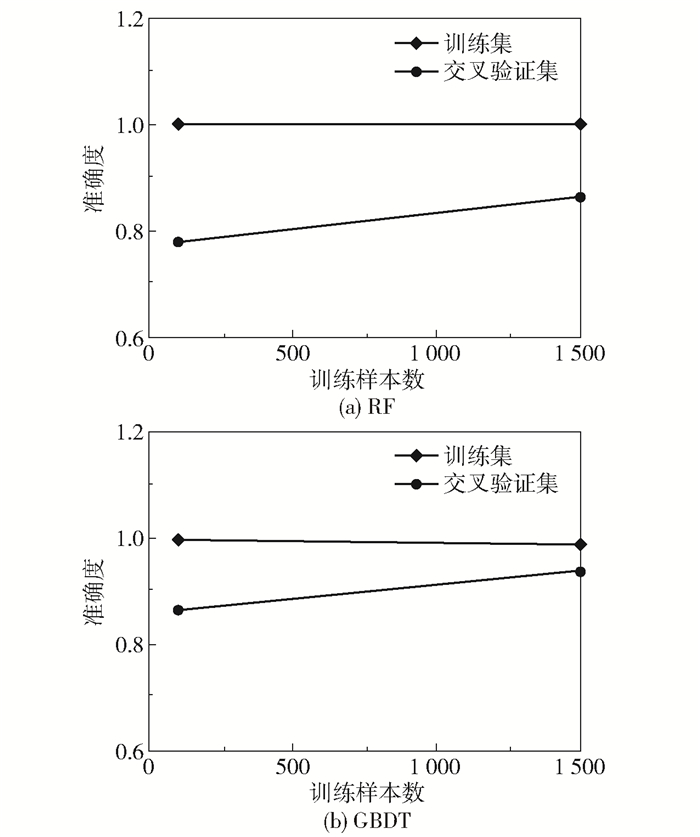
RF是基于套袋(bagging)的思想，有放回地均匀取样，而GBDT则是基于梯度提升(boosting)的思想，根据训练错误率对样本赋予不同的权重。实验所选取的验证集是在数据训练进行有放回抽取时未被抽取的数据的集合，这些未被抽到的材料数据称作袋外数据^[16]。绘制RF和GBDT这两种较优模型的学习曲线，如图 5所示。由图可知，GBDT模型相对于RF模型的学习效果更好。在RF模型中，训练集的准确度在训练过程中基本保持不变，说明该模型在训练过程中拟合程度较好；而交叉验证集的准确度则是从较低的数值逐渐上升的，且并没有无限接近训练集的准确度，两者之间的间距较大，导致误差比较大。也即在训练过程中，RF模型的拟合准确度非常高，达到100%，但是在交叉验证过程中仅达到90%左右。这说明RF模型对于新的数据集适应性较差，存在过拟合的问题。而对于GBDT模型，训练集的准确度在训练过程中有微小的下降，而交叉验证集的准确度则有所上升，且两者有向同一准确度值靠近的趋势(两条数据线趋近的准确度值在95%左右)。由此可见，GBDT模型能够改善RF模型中存在的过拟合现象。

图 5(Fig. 5)

图 5 RF与GBDT模型的学习曲线 Fig.5 Learning curves of RF and GBDT models

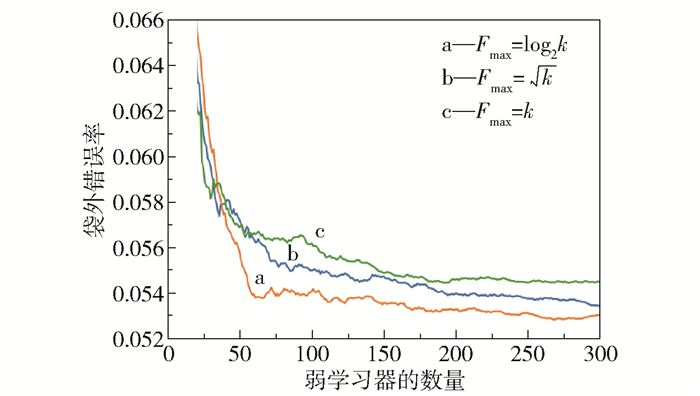
图 6给出了弱学习器的数量n_e与特征向量的种类数F_max对袋外错误率R_e，OOB的影响。袋外错误率是测试数据误差的无偏估计，用来检验RF模型的泛化能力。同时，选择3种不同的方式计算每棵树节点上的特征数量，设总特征数为k，3种方式分别为F_max=log₂k，F_max=$\sqrt k $，F_max=k。从图 6可以看出，3条曲线的变化趋势大致相同，都是随着n_e的增加，R_e，OOB不断下降。当n_e的值增加到70时，曲线c的R_e，OOB要明显高于曲线a、b，说明在每棵树的分裂节点上选择数据集的全部特征很容易使得模型更加复杂，容易产生过拟合现象，造成R_e，OOB较高。而在分裂节点上对于特征的数量的选择则可有效降低模型的复杂程度，避免发生模型的过拟合现象。当n_e的值大于100时，曲线a的R_e，OOB值可以降到最低。当n_e=150，且F_max=log₂k时，就能够有效改善RF模型的性能。

图 6(Fig. 6)

图 6 不同参数对RF模型的影响 Fig.6 Effect of different parameters on the RF model

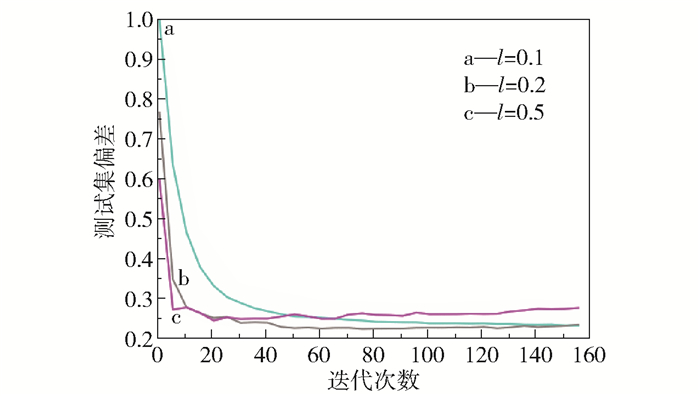
影响GBDT模型拟合效果的两个最重要的因素分别为迭代次数n和每棵回归树的学习速率l，因此本文考察了这两个因素对测试集偏差e的影响。从图 7可以看出，不同学习速率下曲线的变化趋势大致相同，即随着n的增加，e值是逐渐减小的。当n小于20时，3条曲线的e值下降得非常快；而且l=0.5时对应的偏差值是最低的，说明在有限的迭代次数内，l越高，所达到的测试效果越好。而在n大于40时，l=0.5曲线对应的e值一直维持在较高的水平，而l=0.1和l=0.2曲线仍然有下降的趋势。l=0.2曲线在迭代100次左右后偏差达到最低，而l=0.1曲线在迭代140次左右时偏差达到最低。这说明当回归树的l较低时，要增加n的值才能保证e值降低。因此，在训练模型时，可以调节回归树的学习速率l和迭代次数n两个参数来改善GBDT模型。在本文测试中，当n=100，l=0.2时，可以达到有效改善模型性能的效果。

图 7(Fig. 7)

图 7 不同参数对GBDT模型的影响 Fig.7 Effect of different parameters on the GBDT model

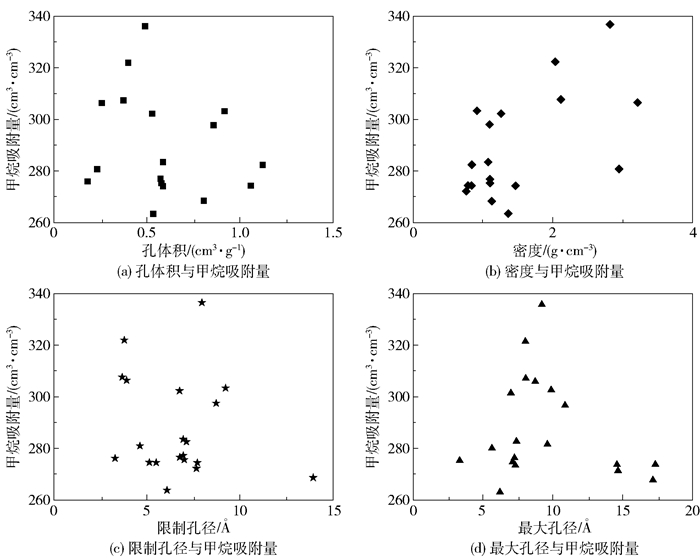
对影响甲烷吸附量的重要度进行分析发现，影响甲烷气体吸附的主要因素为材料的孔体积、密度、限制孔径及最大孔径。利用GBDT模型筛选测试集内的高性能材料，分析前20种高性能材料的特征向量与甲烷吸附量之间的关系，结果如图 8所示。从图中可以看出，当孔体积为0.5~0.75 cm³/g，限制密度为2~3 g/cm³，材料孔径在4 Å左右，最大孔径在6~10 Å时，甲烷的吸附量较高。

图 8(Fig. 8)

图 8 高性能材料的特征向量与甲烷吸附量的关系 Fig.8 Relationship between the feature vectors and methane adsorption of high-performance materials

本文采用DT模型及其衍生的RF、ET、GBDT模型对金属有机框架材料进行分类筛选，通过对模型的筛选性能进行比较，得出GBDT模型的筛选效果最好。当迭代次数为100，学习速率为0.2时，GBDT的模型性能最佳。利用GBDT模型筛选出的前20种金属有机框架材料进行构效关系分析，得出当孔体积为0.5~0.75 cm³/g，材料密度为2~3 g/cm³，材料限制孔径在4 Å左右，最大孔径在6~10 Å时，甲烷的吸附量较高。所得结果可望为用于甲烷吸附的金属有机框材料的设计提出合理化建议。