20世纪80年代,Etsion等[1-2]详细研究了锥度端面密封的性能参数,首次从理论上给出了锥度密封的可行性。迈尔[3]提出了载荷和温度是影响端面变形主要因素的论断,并利用圆环理论来计算密封端面的变形情况。Jang等[4]给出了密封环发生变形时的临界速度,并采用热弹流分析法进行处理,但忽略了冷却液所引起的密封环周围介质的流动的影响。Metcalfe[5]采用影响系数法并考虑密封系统组件间的约束及受力情况,将端面变形归为受各参数的综合影响所致,并计算出密封环各点的变形值。Chen等[6]研究了载荷、环结构与约束条件下密封环的整体变形对其密封性能的影响情况,提出端面变形能使流体膜呈现发散的变化规律,又指出约束对密封环变形具有较大影响。Blasbalg等[7]采用有限元软件对密封环的温度场与端面变形情况进行研究,结果显示端面变形受温升的影响极大,同时环结构设计也对环变形有较大的影响。Harp等[8]构建了瞬态工况下液体静压型端面密封理论模型,利用影响系数法来研究端面的变形规律。Blasiak等[9]使用位移传感器及压电制动装置测量得到了非接触式流体机械密封的端面变形量,并得出角速度和环材质对端面温升影响程度相近的结果。宁秀秀等[10]对螺旋槽流体膜密封的气膜温度、压力、端面变形及性能随压力、转速和环境温度的变化规律进行了研究,得出了在高压高速和高速低压时端面分别形成发散间隙和收敛间隙的结论。马希金等[11]利用pro/e商用软件构建出密封环三维几何模型,探究施加载荷对密封环变形的影响情况,结果表明密封环的最大变形量会发生在两端面的接触部位,且动、静圆环及组件耦合的变形会随含气率的增加而变大。彭旭东等[12]系统地探究了各种结构和约束条件下密封环变形对性能的影响状况。孟祥铠等[13]考虑了辅助O形圈对密封环受力情况的影响,利用整体接触有限单元法构建数学模型,计算不同膜压工况下密封端面的变形规律。陈汇龙等[14]建立了非接触式动压端面密封双向流/固耦合结构模型并进行理论模拟,对比了耦合前后的流场,系统研究了端面变形对膜压脉动所产生的影响情况。于明彬[15]构建了轴向和径向模式的端面密封三维力学模型,在考虑面接触及液膜空化现象的基础上,对膜压分布与表面变形进行流/固耦合的模拟研究。路圣盛[16]利用多目标算法来优化分析密封环的宏观结构对其机械密封性能的影响,得到载荷系数、环厚度与环径等参数对端面变形及密封性能影响较大的结论。Ma等[17]利用数值模拟方法分析了T型槽气膜密封的弹性流体动力特性,并在考虑密封环弹性变形及阻塞效应的条件下计算出气膜压力与温度场的分布情况。
综上所述,国内外学者对密封环变形的研究已有较长的历史且非常系统,但相关研究大多集中于二维建模,或直接采用商用软件进行三维建模,使得研究方式、计算特设条件及结果结论等均存在一定的局限性,与实际情况存在相应的偏差。针对此问题,本文将商业软件与计算机语言编程(满足实际工况中的特设条件及特定的密封结构等)有机结合,尽可能与实景相符合,提出一种端面锥/孔组合型机械密封端面织构,在高、低压工况下研究该种密封的三维流/固耦合模型的端面变形及密封性能的变化规律,以完善非接触式机械密封的设计理论。
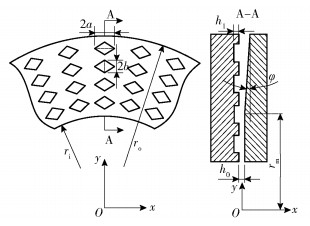
1 密封系统的结构与理论模型 1.1 结构模型图 1所示为锥/孔组合型机械密封端面局部结构图,静、动密封环端面上分别加工出锥度及菱形孔,且孔沿周向呈对称、径向等距分布,定义锥度ϕ=(ro-rm)*tanφ/h0[18],锥面宽度比γ=(ro-rm)/(ro-ri),坐标系x、y轴分别沿圆周、半径方向。其中,φ为锥角,ri、ro、rm分别为内、外半径及无锥区半径。
|
图 1 端面织构分布示意图 Fig.1 Schematic diagram of the end face texture distribution |
非孔区端面间液体基础膜厚为h0,菱形孔深度为h1,对称轴半长轴为a,半短轴为b,分别表示菱形孔的结构特征,设定长短轴比ξ为
| $ \xi = a/b $ | (1) |
密封环边界条件为周期性边界条件,静密封环采用固定约束,动密封环采用指定位移,在运行中会随轴的振动而发生偏转、不对中现象,同时受弹簧力和外压的作用,端面施加力为液膜压力。
1.2 理论模型假设端面间流体压力沿膜厚方向恒定不变;密封流体为牛顿型流体,黏度始终保持不变,则用于描述端面膜压的控制方程为
| $ \frac{\partial }{{\partial x}}\left( {\frac{{{h^3}}}{{6\mu }}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{{h^3}}}{{6\mu }}\frac{{\partial p}}{{\partial y}}} \right) = U\frac{{\partial h}}{{\partial x}} + V\frac{{\partial h}}{{\partial y}} $ | (2) |
式中,p为端面膜压;U、V分别为x和y方向上端面平均线速度;h为膜厚;μ为密封介质黏度系数。
膜厚方程
| $ h = \left\{ {\begin{array}{*{20}{l}} {{h_0} - {h_i} + {h_j},}&{{\rm{孔外无锥度区}}}\\ {{h_0} - {h_i} + {h_j} + {h_k},}&{{\rm{孔外有锥度区}}}\\ {{h_0} + {h_1} - {h_i} + {h_j},}&{{\rm{孔内无锥度区}}}\\ {{h_0} + {h_1} - {h_i} + {h_j} + {h_k},}&{{\rm{孔内有锥度区}}} \end{array}} \right. $ | (3) |
式中,hi、hj和hk分别为动、静圆环端面上某点的变形值以及锥面高度。
当系统稳定运行时,动密封环组件轴向受力平衡,即
| $ {F_{\rm{c}}} = {F_{\rm{o}}} $ | (4) |
其中,
| $ {{F_{\rm{c}}} = {\rm{ \mathit{ π} }}\left( {r_{\rm{o}}^2 - r_{\rm{i}}^2} \right)\left[ {{p_{{\rm{sp}}}} + B\left( {{p_{\rm{o}}} - {p_{\rm{i}}}} \right)} \right]} $ | (5) |
| $ {{F_{\rm{o}}} = {p_{\rm{a}}}{A_{\rm{a}}}N\iint p {\rm{d}}x{\rm{d}}y} $ | (6) |
式中,Fc为端面闭合力;Fo为端面开启力;pi、po分别为内、外压;psp为弹簧比压;B为平衡比;Aa为单菱形孔截面面积;pa为环境或空化压力;N为计算周期。
设环变形为弹性变形,变形控制方程如下[19]。
应力平衡方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial y}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}} + X = 0}\\ {\frac{{\partial {\tau _{yx}}}}{{\partial x}} + \frac{{\partial {\sigma _y}}}{{\partial y}} + \frac{{\partial {\tau _{yz}}}}{{\partial z}} + Y = 0}\\ {\frac{{\partial {\tau _{zx}}}}{{\partial x}} + \frac{{\partial {\tau _{zy}}}}{{\partial y}} + \frac{{\partial {\sigma _z}}}{{\partial z}} + Z = 0} \end{array}} \right. $ | (7) |
式中,σx、σy、σz为正应力;τxy、τxz、τyz为切应力。
几何方程
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{{\partial u}}{{\partial x}},{\gamma _{xy}} = {\gamma _{yx}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}}\\ {{\varepsilon _y} = \frac{{\partial v}}{{\partial y}},{\gamma _{yz}} = {\gamma _{zy}} = \frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}}\\ {{\varepsilon _z} = \frac{{\partial w}}{{\partial z}},{\gamma _{zx}} = {\gamma _{xz}} = \frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \end{array}} \right. $ | (8) |
式中,εx、εy、εz为正应变;γxy、γyz、γzx为切应变;u、v、w为位移变量。
物理方程
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{1}{E}\left[ {{\sigma _x} - \nu \left( {{\sigma _y} + {\sigma _z}} \right)} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\gamma _{xy}} = \frac{{{\tau _{xy}}}}{G}}\\ {{\varepsilon _y} = \frac{1}{E}\left[ {{\sigma _y} - \nu \left( {{\sigma _z} + {\sigma _x}} \right)} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\gamma _{yz}} = \frac{{{\tau _{yz}}}}{G}}\\ {{\varepsilon _z} = \frac{1}{E}\left[ {{\sigma _z} - \nu \left( {{\sigma _x} + {\sigma _y}} \right)} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\gamma _{zx}} = \frac{{{\tau _{zx}}}}{G}} \end{array}} \right. $ | (9) |
式中,E为弹性模量;ν为泊松比;G为剪切弹性模量。
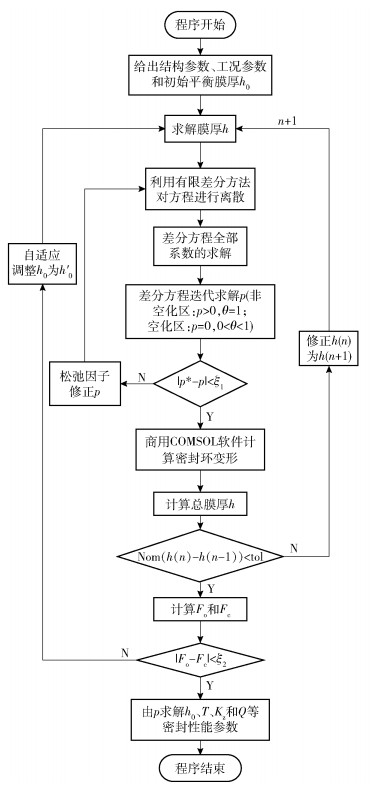
将式(2)~(9)进行联合离散求解得出p,并作用于动、静密封环端面上使其轴向受力平衡;利用Matlab自行编程计算膜压p,再通过商用有限元软件COMSOL分别计算动、静密封环的变形量,以变形后的膜厚重新求解p;反复迭代求解,直到前后两次求解的Fo和h小于给定误差,即停止计算,输出端面变形;以最终求出的p来计算液膜刚度Kz、泄漏率Q和摩擦扭矩T等性能参数,并同时研究ϕ、锥面宽度比γ和环变形等对密封性能的影响规律。计算流程如图 2所示。
|
图 2 锥孔组合型机械密封环变形及性能计算流程图 Fig.2 Computational flow chart of end face deformation and performance of the cone-pore combined mechanical seal |
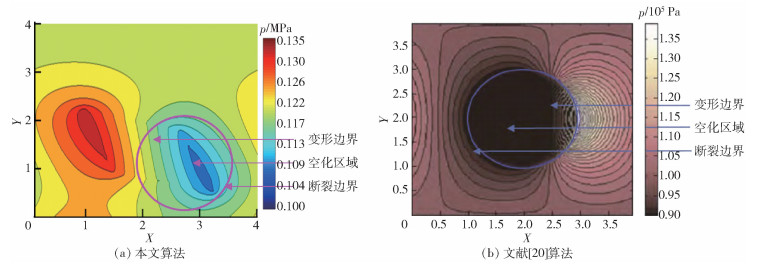
为证明自编程序算法的正确性,采用文献[20]中对应参数及孔型模型对运算程序进行准确性验证,即在圆形微孔半径r=37.5 mm,孔深h1=4 μm,po、pi均为0.1 MPa及转速ω为300 r/min的操作工况下进行膜压场的计算。由图 3(a)、(b)对比可知,计算得到的空化区域及压力分布云图与文献[20]的具有相似性,且峰、谷值的压力相差约为7.5%,故可验证程序的正确性。
|
图 3 本文算法与文献[20]算法圆形微孔压力分布对比 Fig.3 Comparison of pressure distributions with one spherical dimple for our algorithm and that in Ref. [20] |
设置结构参数与操作参数如下。
结构参数ri=127.5 mm,ro=141.5 mm;菱形织构孔的半长轴a=2 mm,孔的深度h1=1.25 μm,单列孔数ns=4,长短轴比ξ=1.67,动、静密封环弹性模量E1=617 GPa、E2=23 GPa,环厚度均为hb=10 mm,泊松比ν1=0.28、ν2=0.25,ϕ=1,γ=1,B=0.9,psp=0.1,N=151。
操作参数pi=0.101 MPa,低压时po=0.3 MPa,高压时po=6.6 MPa,μ=0.001 Pa·s(25 ℃的清水),动密封环转速ω=1 500 r/min;在计算时采取低压低速,高压采用低、中、高速3档,除文中特殊说明外参数值均按此规定。
以动、静密封环的轴中心线为三维坐标轴的z轴,规定密封端面变形位移量在z轴方向上变化,z轴即为变形方向轴,各自原密封端面处为0基准点,整个密封端面为x/y轴平面,拉伸变形为正值,压缩变形为负值。
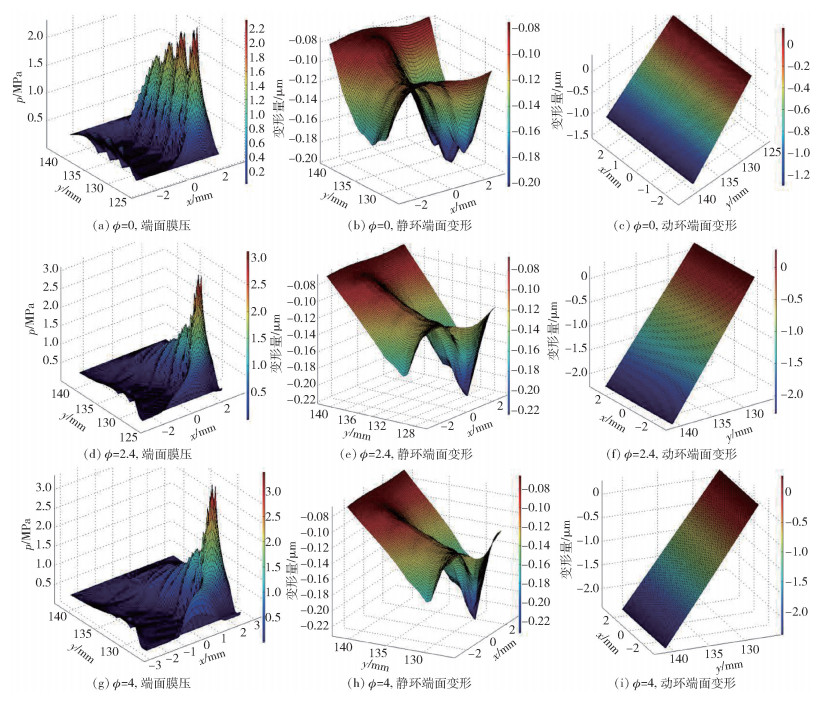
2.1 收敛锥度ϕ对端面变形的影响图 4示出了转速ω=1 000 r/min、不同ϕ下的密封端面变形及膜压场的变化情况。由图可知,因菱形孔的存在能够使端面间液膜产生极强的动压效应,在研究工况范围内膜压场的最高压力峰值随着ϕ的增大不断增大,高压区范围不断缩小,低压区范围不断扩大,且高压区范围沿外径处向内径处移动,即形成压场的峰值越来越陡峭。这表明随ϕ的增大流体静压效应的作用范围逐渐向内径处扩大,靠近外径侧的动压效应则被相应削弱,但越接近内径处,由于膜厚不断减小,因挤压产生的动压效应就逐渐增大。另外还可以看出,静密封环端面由于受到膜压场的压力作用形成有规律的凸凹曲面,且变形情况与膜压场的形状类似,膜压大的区域对应端面的变形就大,压力小的区域产生的端面变形就小;而动密封环在径向方向上产生倾斜变形,ϕ越大则变形越大。由图 4(a)~(i)知,当ϕ=0、2.4和4时,因端面上菱形孔和锥度的存在,产生明显的动压和静压效应,使得静密封环端面上产生了周期性波式变形和倾斜锥度变形,且波幅值要大于内、外径处的变形量,最大变形量靠近内径侧,分别为0.211 μm、0.223 μm和0.236 μm;动密封环端面锥度变形比较明显,波式变形较不明显,且随着ϕ的增大,锥度变形也越来越大。原因在于动密封环硬度要大于静密封环硬度,故而动密封环波式变形没有静密封环的明显,而且动密封环在轴向方向上受到弹簧力及液压等的推动,转动过程中密封环发生偏斜,使得动密封环端面径向锥度变形明显,波式变形减弱。
|
图 4 ϕ变化时的端面变形及膜压图 Fig.4 Schematic of seal face deformation and fluid film pressure for different extents of face taper |
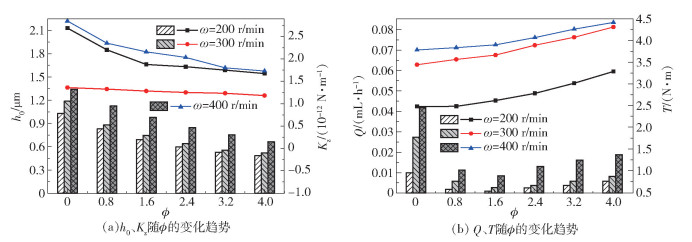
图 5示出了低压(po=0.3 MPa)下,考虑端面变形时ϕ对密封性能的影响规律。结果显示,在低转速时,随ϕ的不断增大,h0和Kz逐渐减小,Q为先减小后增大,具有最小泄漏率,而摩擦扭矩T则是逐渐增大。原因在于随着ϕ的增大,膜厚呈锥形变化,近外径侧变大,内径侧变小,静压差对端面液膜的影响范围加大,靠近外径侧的动压效应减弱,靠近内径侧的动压效应和T因h0不断变小而变大,故而整个端面受压不均,液膜稳定性变差。当ϕ=0.8~1.6时,Kz较大,Q和T较小。还可看出,在ϕ相同时,ω增大,h0、Q和T随之增大,Kz值大小顺序则为Kz(ω=300 r/min)<Kz(ω=200 r/min)<Kz(ω=400 r/min)。这表明ω增大则动压效应增大,导致h0、Q和T变大,而Kz随ω的变大变化趋势却略有不同,这是由于ω较低时,靠近外径侧的静压效应占主导地位,液膜稳定性较强,故Kz(ω=300 r/min)<Kz(ω=200 r/min);当ω=400 r/min时,h0的增大削弱了ω增大所带来的动压效应,液膜压场分布较均匀,液膜稳定性变好,相应的Kz(ω=400 r/min)也较大。因此对经常启闭或低速旋转设备,应选取带收敛锥面的密封环,最佳锥度ϕ取值范围为0.8~1.6。
|
柱状图对应左侧坐标轴,曲线图对应右侧坐标轴。 图 5 锥度ϕ对密封性能的影响 Fig.5 Effect of face taper on sealing performance parameters |
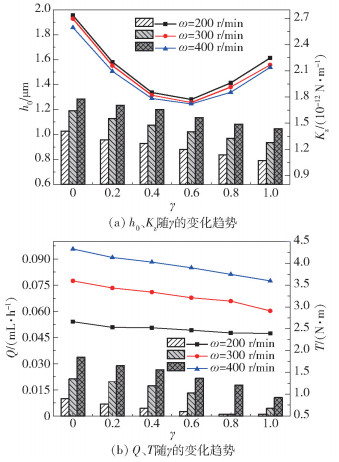
图 6示出了低压(po=0.3 MPa)下,考虑端面变形时γ对密封性能的影响规律。由图可知,随着γ的增大,h0、Q和T缓慢减小,而Kz随γ的增加先减后增,具有极小值。这说明密封端面带有部分锥度,则相当于在一定程度上减小了环面宽度,即闭合力减小,对应的端面间液膜支撑环的开启力减弱,h0和T就会变小,导致Q相应减小。随γ的增大,端面内静压效应影响的范围扩大,动压效应相应减弱,微小扰动减弱,导致Kz变小;当γ增大到一定程度时,随着h0的减小,靠近内径层的动压效应增强,内径处的变形增大,微小扰动增强,故而Kz又逐渐变大。还可看出,γ相同时,随着ω的增大,h0、Q和T是不断增大的,Kz逐渐减小。这说明随ω增大,动压效应逐渐增大,h0较大,致使Q变大,但同时h0增大会削弱端面间液膜的动压效应,当增加的动压效应小于削弱的动压效应时,微小扰动减弱,相应Kz就会变小。故而对于低压、低速设备,为保证液膜稳定性及密封可靠性,应选取带有部分锥度的端面,γ取值范围为0.8~1。
|
柱状图对应左侧坐标轴,曲线图对应右侧坐标轴。 图 6 γ对密封性能的影响 Fig.6 Effect of γ on sealing performance parameters |
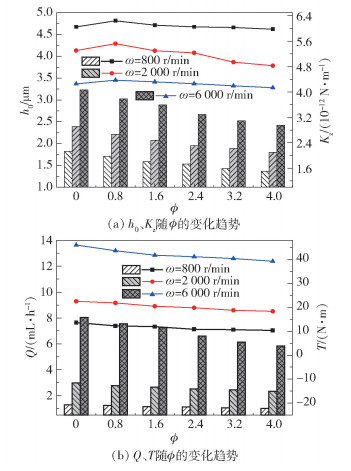
图 7示出在高压(po=6.6 MPa)下,考虑端面变形时ϕ对密封性能的影响情况。由图可知,随着ϕ的增大,h0、Q和T缓慢减小,而Kz则是先略微增大后缓慢减小,并在ϕ=0.8时达到极大值。还可看出,ϕ值相同时,ω越高,h0、T和Q越大,而Kz却变小。这说明靠近内径处端面间液膜的动压效应随ω的增大而增强,但外径侧的动压效应受到静压差的影响,增大程度远小于内径侧,导致整个端面受压严重不均,致使液膜不稳,故而转速越大,Kz就越小。对于较高速、高压旋转设备的机械密封系统,为达到较好的液膜稳定性和密封可靠性,应选取静环的ϕ=0.8~1.6为宜。
|
柱状图对应左侧坐标轴,曲线图对应右侧坐标轴。 图 7 ϕ对密封性能的影响 Fig.7 Effect of ϕ on sealing performance parameters |
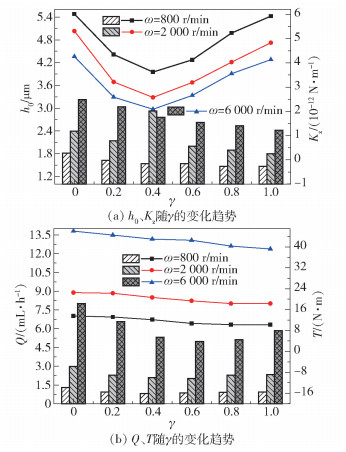
图 8示出在高压(po=6.6 MPa)下,考虑端面变形时γ对密封性能的影响情况。由图可知,随着γ的增大,h0和T逐渐减小,而Q和Kz先减小后增大,且分别在γ=0.6和γ=0.4时具有极小值。还可以看出,γ相同时,随ω的增大,h0、T和Q增大,而Kz却逐渐减小。为使密封系统的稳定性和密封性效果均较好,应选取转速和压强较高的旋转设备的机械密封系统,为达到较好的液膜稳定性和密封可靠性,应选取静环γ=0.6~1为宜。
|
柱状图对应左侧坐标轴,曲线图对应右侧坐标轴。 图 8 γ对密封性能的影响 Fig.8 Effect of γ on sealing performance parameters |
(1) 在研究工况范围内,因端面上菱形孔和锥度的存在,产生明显的动压和静压效应。随ϕ的增大,高压区缩小,低压区扩张,形成的压力峰值越来越陡峭,使得静密封环端面上产生了周期性波式变形和倾斜锥度变形,变形情况与膜压场的形状类似;动密封环端面锥度变形比较明显,波式变形不明显,且随ϕ的增大,锥度变形程度也越来越大。
(2) 对于经常启闭、低压或低速旋转设备,为保证液膜稳定性及密封可靠性,应选取带收敛锥面的密封环,其中ϕ=0.8~1.6、γ=0.8~1为佳。对于较高速、高压旋转设备的机械密封系统,为达到较好的液膜稳定性和密封可靠性,应选取ϕ=0.8~1.6、γ=0.6~1为宜。
| [1] |
ETSION I, SHARONI A. Performance of end-face seals with diametral tilt and coning-hydrostatic effects[J]. ASLE Transactions, 1980, 23(3): 279-288. DOI:10.1080/05698198008982970 |
| [2] |
ETSION I. Dynamic analysis of noncontacting face seals[J]. Transacions of the ASME, 1982, 104: 460-468. |
| [3] |
迈尔. 机械密封[M]. 北京: 化学工业出版社, 1981. MAYER E. Mechanical seal[M]. Beijing: Chemical Industry Press, 1981. (in Chinese) |
| [4] |
JANG J Y, KHONSARI M M. A generalized thermoelastic instability analysis[J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 2003, 459: 309-329. |
| [5] |
METCALFE R. End-face seal deflection effect-the problems of two-component stationary or rotating assemblies[J]. ASLE Transactions, 1980, 23(4): 393-400. DOI:10.1080/05698198008982984 |
| [6] |
CHEN Z, LIU T C, LI J M. The effect of the O-ring on the end face deformation of mechanical seals based on numerical simulation[J]. Tribology International, 2016, 97: 278-287. DOI:10.1016/j.triboint.2016.01.038 |
| [7] |
BLASBALG D A, SALANT R F. Numerical study of two-phase mechanical seal stability[J]. Tribology Transactions, 1995, 38(4): 791-800. DOI:10.1080/10402009508983472 |
| [8] |
HARP S R, SALANT R F. Analysis of mechanical seal behavior during transient operation[J]. Journal of Tribology, 1998, 120(2): 191-197. DOI:10.1115/1.2834409 |
| [9] |
BLASIAK S, LASKI P A, TAKOSOGLU J E. Parametric analysis of heat transfer in non-contacting face seals[J]. International Journal of Heat and Mass Transfer, 2013, 57: 22-31. DOI:10.1016/j.ijheatmasstransfer.2012.09.058 |
| [10] |
宁秀秀, 何鹏刚, 白少先. 螺旋槽端面气膜密封结构高温特性研究[J]. 航空发动机, 2019, 45(2): 13-18. NING X X, HE P G, BAI S X. Study on high temperature characteristics of spiral groove end surface gas film seal structure[J]. Aeroengine, 2019, 45(2): 13-18. (in Chinese) |
| [11] |
马希金, 包春辉, 贾维斌. 基于流固耦合油气混输泵双端面机械密封的变形分析[J]. 甘肃科学学报, 2017, 29(3): 114-116, 124. MA X J, BAO C H, JIA W B. Deformation analysis on double mechanical seal of oil-gas multiphase pump based on fluid-structure interaction[J]. Journal of Gansu Sciences, 2017, 29(3): 114-116, 124. (in Chinese) |
| [12] |
彭旭东, 冯向忠, 胡丹梅, 等. 非接触式气体润滑密封变形的数值分析[J]. 摩擦学学报, 2004, 24(6): 536-540. PENG X D, FENG X Z, HU D M, et al. Numerical analysis of deformation of a non-contacting gas lubricated seal[J]. Tribology, 2004, 24(6): 536-540. (in Chinese) |
| [13] |
孟祥铠, 吴大转, 王乐勤. 辅助密封影响下机械密封端面变形行为的研究[J]. 润滑与密封, 2008, 33(1): 101-103. MENG X K, WU D Z, WANG L Q. Study on deformation behavior of mechanical seal faces influenced by secondary seals[J]. Lubrication Engineering, 2008, 33(1): 101-103. (in Chinese) |
| [14] |
陈汇龙, 李同, 任坤腾, 等. 端面变形对液体动压型机械密封液膜瞬态特性的影响[J]. 化工学报, 2017, 68(4): 1533-1541. CHEN H L, LI T, REN K T, et al. Influence of end face deformation on transient characteristics of fluid film in hydrodynamic mechanical seal[J]. CIESC Journal, 2017, 68(4): 1533-1541. (in Chinese) |
| [15] |
于明彬. 核主泵用深槽端面机械密封性能理论研究[D]. 杭州: 浙江工业大学, 2010. YU M B. Theoretical study on the performance of mechanical seals with deep grooves used in reactor coolant pump[D]. Hangzhou: Zhejiang University of Technology, 2010. (in Chinese) |
| [16] |
路圣盛. 基于流固耦合的动压型机械密封多目标优化研究[D]. 镇江: 江苏大学, 2019. LU S S. Study on multi-objective optimization of hydrodynamic mechanical seal based on fluid-structure interaction[D]. Zhenjiang: Jiangsu University, 2019. (in Chinese) |
| [17] |
MA C H, BAI S X, PENG X D. Thermoelastohydrody-namic characteristics of T-grooves gas face seals[J]. International Journal of Heat and Mass Transfer, 2016, 102: 277-286. DOI:10.1016/j.ijheatmasstransfer.2016.06.034 |
| [18] |
彭旭东, 刘鑫, 孟祥铠, 等. 锥面-微孔组合端面机械密封性能[J]. 化工学报, 2011, 62(12): 3463-3470. PENG X D, LIU X, MENG X K, et al. Performance of mechanical face seals with both surface micropores and convergent coning[J]. CIESC Journal, 2011, 62(12): 3463-3470. (in Chinese) |
| [19] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG M C. Finite element method[M]. Beijing: Tsinghua University Press, 2003. (in Chinese) |
| [20] |
QIU Y, KHONSARI M M. On the prediction of cavitation in dimples using a mass-conservative algorithm[J]. Journal of Tribology, 2009, 131(4): 041702. DOI:10.1115/1.3176994 |







