随着我国石油化工行业的快速发展,承压类特种设备的应用规模日益增长,生产过程中存在的隐患和事故可能带来的危害也越来越大。作为保障生产过程、工厂效益和人员生命安全的核心部分,安全仪表系统(safety instrumentation system,SIS)越来越受到人们的重视[1]。而最终执行元件作为安全仪表系统中的关键组成部分,承担着在紧急情况下执行安全连锁动作的重要任务,如果存在功能安全失效,将会使整个安全仪表系统的功能安全完整性(functional safety integrity)受到影响[2]。因此,最终执行元件的功能安全失效分析对于保障系统的生产安全具有重要的研究价值和实际意义。
当今最为常用的失效模式和影响分析(failure mode and effects analysis,FMEA)方法,就是在产品设计阶段对其子系统、零件或各个工序进行分析,找出潜在的失效模式并分析失效可能造成的影响[3],但对于投入使用后的最终执行元件则有所忽视;而危险与可操作性(hazard and operability,HAZOP)分析方法则以“引导词+参数”的形式,通过生产过程中参数所发生的偏差进行功能安全的定性分析,目前利用HAZOP方法进行定量分析的研究仍处于起步阶段[4];而利用Markov模型的分析方法则是基于状态转换矩阵对系统各个时刻处于某个状态的概率进行估计,并通过计算时刻内的平均概率值而非工况参数所处的实际状况来对功能安全完整性进行定量评价[5]。综上所述,现有方法均存在一定的局限,如何能够在全生命周期(safety life cycle,SLC)内,尤其是在役期间,对最终执行元件功能安全失效进行科学和合理的分析,以保证最终执行元件功能安全的完整性,确保安全仪表系统功能的切实执行,仍是急需解决的关键性问题。
针对现有方法的不足,本文提出一种最终执行元件功能安全失效分析方法,构建最终执行元件功能安全完整性的在线检测系统,利用工况参数所构成的表征参数向量,基于经过变换的马氏距离构建失效表征模型,并确定最终执行元件当前所处的状态,实现安全仪表系统最终执行元件的功能安全失效分析,最后对此方法进行验证。
1 基于马氏距离的功能安全检测方法 1.1 马氏距离马氏距离(Mahalanobis distance)是一种通过计算样本间的协方差距离度量其相似性的广义距离。马氏距离越大,样本间相似性越小;马氏距离越小,则样本间的相似性越大。马氏距离具有平移不变性、旋转不变性和仿射不变性这3个性质[6]。
对于一个样本向量x,其到样本集Y的马氏距离为
| $ D=\sqrt{(\boldsymbol{x}-\boldsymbol{Y})^{\mathrm{T}} \boldsymbol{C}^{-1}(\boldsymbol{x}-\boldsymbol{Y})} $ | (1) |
式中,D为变换前的马氏距离;Y为m×n的矩阵,m为样本向量的维度,n为样本集中样本的数目。Y为样本集矩阵的重心,计算式为
| $ \overline{\boldsymbol{Y}}=\frac{1}{n} \sum\limits_{i=1}^{n} \boldsymbol{Y}_{i} $ | (2) |
C为样本集Y的协方差矩阵
| $ C=\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(\boldsymbol{Y}_{i}-\overline{\boldsymbol{Y}}\right)\left(\boldsymbol{Y}_{i}-\overline{\boldsymbol{Y}}\right)^{\mathrm{T}} $ | (3) |
在计算马氏距离时,为保证协方差矩阵存在矩阵的逆,即协方差矩阵为满秩矩阵,构成样本集的样本数量n要大于样本的维度m。
1.2 马氏距离的Box-Cox变换最终执行元件投入使用后,其性能会随时间逐渐退化,动作过程中所检测到的表征参数的实际数值会逐渐偏离正常情况下的参数数值,待测的最终执行元件与功能安全完整的最终执行元件之间马氏距离也会逐渐增大。当马氏距离大于一定的阈值时,则认定该最终执行元件存在功能安全失效,其功能安全完整性受损。
在实际情况下,即使是无失效状态的最终执行元件,各参数数值也不会保持在额定值,而是在一定容差范围内变化。假定参数的变化满足正态分布,根据正态分布的3σ准则,对于一个满足均值为μ、标准差为σ的正态分布的数组,其概率密度曲线(μ-σ, μ+σ)区间内的面积占比为68.27%,(μ-1.96σ, μ+1.96σ)区间内的面积占比为95.45%,(μ-2.58σ, μ+2.58σ)区间内的面积占比为99.73%。基于以上理论进行最终执行元件功能安全完整性状态判别的阈值设定。
Box-Cox变换是一种常用的数据变换,可以将不符合正态分布的变量转换为服从正态分布的变量,其特点是引入一个参数λ,由参数λ来决定变换形式,而参数λ的值根据数据本身进行估计,通过λ的最大似然函数进行计算。Box-Cox变换过程为[7]
| $ {D^\prime } = \left\{ {\begin{array}{*{20}{l}} {\ln D,}&{\lambda = 0}\\ {\frac{{{D^\lambda } - 1}}{\lambda },}&{\lambda \ne 0} \end{array}} \right. $ | (4) |
| $ f(D,\lambda ) = - \frac{n}{2}\ln \left[ {\sum\limits_{i = 1}^n {\frac{{{{\left( {D_i^\prime - {{\bar D}^\prime }} \right)}^2}}}{n}} } \right] + (\lambda - {\rm{ 1) }}\sum\limits_{i = 1}^n {\ln } {D_i} $ | (5) |
式中,D′为变换后的马氏距离,D′为变换后的样本向量均值,
变换后的马氏距离D′服从正态分布N(μ, σ2),如图 1所示。根据3σ准则进行最终执行元件状态的划分,将变换后的马氏距离D′落在映射后的(-∞, μ+1.96σ]区域内的样本视为“健康”;落在(μ+1.96σ, μ+2.58σ]区域内的样本视为“易发生失效”,应当发布预警,及时进行进一步细致检查;而落在(μ+2.58σ, +∞)区域内的样本则认为已经发生失效,同时约有0.135%的概率误判,此时应马上采取措施,防止因最终执行元件的失效而导致生产事故发生。
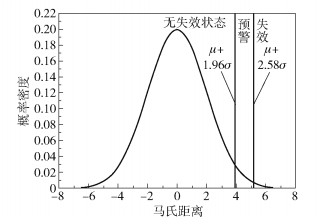
|
图 1 变换马氏距离的阈值划分 Fig.1 Threshold division of the transformation Mahalanobis distance |
基于马氏距离的最终执行元件功能安全完整性失效表征具体实现流程如图 2所示,具体步骤如下:
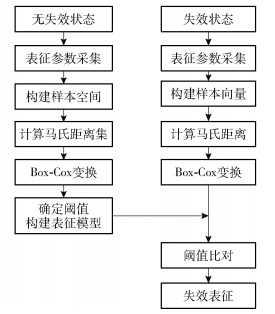
|
图 2 基于马氏距离的失效表征流程图 Fig.2 Flow chart of failure characterization based on Mahalanobis distance |
1) 预先获取无失效状态和失效状态下最终执行元件的各工况参数,构建出样本空间;
2) 计算样本空间中各样本间的马氏距离集;
3) 计算参数λ的最大似然估计,以此决定Box-Cox变换形式,对马氏距离集进行Box-Cox变换,使其满足正态分布;
4) 计算变换后马氏距离集的正态分布均值μ与方差σ,由正态分布的3σ准则确定最终执行元件在不同状态下的阈值,构建最终执行元件的失效表征模型;
5) 利用所设计的最终执行元件功能安全完整性检测系统采集不同时段下失效表征参数的实际数值,以此构建样本向量x(Ii, pj, lk),其中I为电磁阀电流,p为气缸压力,l为执行机构位移,计算样本向量与样本空间的马氏距离,并同样进行Box-Cox变换,根据阈值确定最终执行元件所处状态,实现最终执行元件功能安全失效表征。
即使在单失效假设下,当最终执行元件存在功能安全失效时,仅表现为单个失效参数存在数值的漂移,而其他的失效表征参数还是保持在无失效状态的范围内,其变换马氏距离仍会超过μ+2.58σ的阈值。因此,由变换马氏距离D′构建最终执行元件失效表征模型,如式(6)所示。
| $ \left\{\begin{array}{ll} \text { 无失效状态 }, & \text { if }-\infty<D^{\prime} \leqslant \mu+1.96 \sigma \\ \text { 预警状态, } & \text { if } \mu+1.96 \sigma<D^{\prime} \leqslant \mu+2.58 \sigma \\ \text { 失效状态, } & \text { if } \mu+2.58 \sigma<D^{\prime}<+\infty \end{array}\right. $ | (6) |
典型承压类安全仪表系统最终执行元件如图 3所示,主要由电磁阀、气缸、执行机构和控制阀组成。
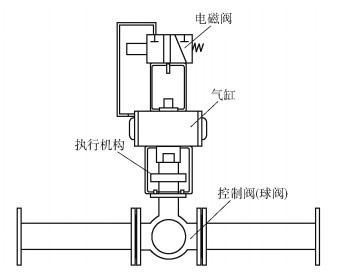
|
图 3 典型承压类安全仪表系统最终执行元件 Fig.3 Final actuator of a typical pressure type safety instrument system |
正常工况下最终执行元件保持静止状态,不会影响到正常的生产过程。一旦安全仪表系统的传感元件检测到生产系统有故障发生的可能,逻辑单元会及时发出控制指令,控制最终执行元件做出切断动作。此时,驱动电磁阀切换状态,排出气缸内的气体,执行机构就会在弹簧的作用力下带动控制阀切断工艺管道,实现最终执行元件的安全功能。
2.2 检测系统最终执行元件功能安全完整性检测系统的结构组成如图 4所示。
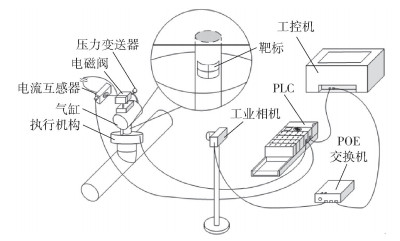
|
图 4 最终执行元件功能安全完整性检测系统 Fig.4 Functional safety integrity testing system for the final actuator |
最终执行元件功能安全完整性检测系统主要由传感元件、可编程逻辑控制器(programmable logic controller,PLC)、工控机等构成。其中传感元件包括开合式的穿心电流互感器、压力变送器、扭矩传感器和机器视觉系统。穿心电流互感器和压力变送器实时采集电流和压力参数,以标准4~20 mA信号输送至PLC;机器视觉系统则由工业相机、以太网供电(power over ethernet,POE)交换机组成,工业相机由POE交换机供电并实时采集执行机构的动作图像,图像数据利用GigE接口由交换机传至工控机中,通过预先固定在执行机构上的靶标的位移计算出执行机构的位移量。分析时所需要用到的工况参数如表 1所示,电磁阀线圈电流、气缸压力、执行机构角位移等3个参数对最终执行元件工作性能的影响程度最大,它们的变化将直接影响到最终执行元件的安全功能执行,进而影响到整个安全仪表系统的功能安全完整性,因而将这3个参数选取为功能安全失效表征参数,通过这些参数进行最终执行元件的功能安全失效表征。PLC将采集到的工况参数通过OLE for process control(OPC)协议发送至工控机进行分析,并承担在检测时对最终执行元件进行控制的任务。
| 下载CSV 表 1 失效分析所用的参数 Table 1 Parameters used in failure analysis |
进行检测时,预先将原有安全仪表系统切换至检测系统,对最终执行元件进行控制。由检测系统程序发出控制信号,临时切断电磁阀的供电,由于系统存在一定的延迟,控制阀不会立刻完全切断工艺管道。在最终执行元件的动作到达一定阈值之前,传感元件实时采集工况参数,一旦到达所设定阈值,检测系统程序立刻发出控制信号,还原系统供电,使系统恢复初始状态。通过此种方式进行测试不会对工艺管道造成显著影响。
进行动作检测时,将各参数在不同时段下所采集到的数值作为样本向量中的元素,分别相对各个参数在无失效状态下检测的数值所组成的样本集进行变换后马氏距离的计算,实现最终执行元件功能安全失效的分析与评价。
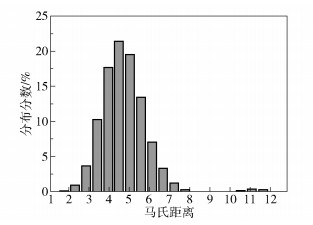
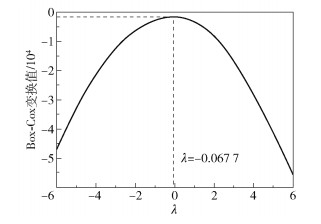
3 实验验证 3.1 仿真实验验证利用Simulink软件对典型安全仪表系统最终执行元件的动态过程进行仿真,在动作过程中选取最终执行元件的电磁阀电流I、气缸压力p及执行机构位移l的各4个仿真数据点,并在此基础上通过添加合理的高斯噪声,模拟不同状态下工况参数的变化,生成200组仿真数据,构成样本空间Y,如表 2所示。计算该样本空间的马氏距离,其柱状分布图如图 5所示,可以看出马氏距离并不服从正态分布。对λ进行最大似然估计,其结果如图 6所示,可得参数λ的值为-0.067 7。进行Box-Cox变换,将马氏距离映射到均值μ=1.452 4,标准差σ=0.217 2的正态分布中。
| 下载CSV 表 2 样本空间部分数据 Table 2 Partial sample space data |
|
图 5 马氏距离柱状图 Fig.5 Histogram of Mahalanobis distance |
|
图 6 λ的最大似然估计 Fig.6 Maximum likelihood estimation of λ |
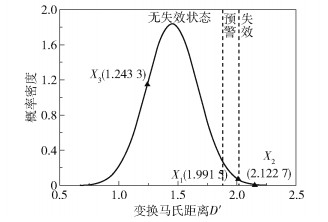
以同样的方式仿真构建另外3组未知状态下的数据作为要进行失效分析的样本向量,根据所构建的失效表征模型进行最终执行元件的失效表征。3组待测数据分别为:X1=[0.020 4, 0.056 0, 0.131 6, 0.268 6, 130 117, 172 702, 194 801, 197 774, 0.177 8, 0.305 3, 0.376 8, 0.389 8],X2=[0.020 8, 0.055 6, 0.133 7, 0.268 5, 129 968, 172 791, 194 901, 197 745, 0.167 4, 0.301 6, 0.389 0, 0.390 9],X3=[0.020 9, 0.056 0, 0.132 2, 0.267 9, 130 064, 172 748, 194 879, 197 703, 0.176 3, 0.305 8, 0.380 1, 0.393 5]。
分别计算3组样本向量对样本空间的马氏距离,并进行同样的Box-Cox变换,其结果如图 7所示。由X1、X2、X3所计算的变换马氏距离分别为1.991 5,2.122 7,1.243 3。由失效表征模型可知,X1处于预警状态,易发生失效;X2已经存在功能安全失效,其功能安全完整性受到了影响;X3则处于无失效状态。
|
图 7 失效表征模型实验分析结果 Fig.7 Experimental analysis of the failure characterization model |
在实际工况条件下对典型安全仪表系统最终执行元件的动态过程进行检测,如图 8所示。在现场对基于马氏距离的功能安全检测方法进行实际测试并验证其有效性。

|
图 8 现场实际测试 Fig.8 View of the practical on-site test rig |
在实验现场对最终执行元件动作过程中气缸压力p1、进气口压力p2、执行阀扭矩T及执行机构位移l的各4个实际数据点进行数据采集,生成100组真实数据,构成样本空间。计算该样本空间的马氏距离,并对λ进行最大似然估计,可得参数λ的值为0.811 9。进行Box-Cox变换后,将马氏距离映射到均值μ=3.632 6,标准差σ=1.062 2的正态分布中。
在现场对执行阀的电磁制动器施加作用,模拟执行阀发生卡堵故障的工况,同时采集制动后的气缸压力、进气口压力、执行阀扭矩及执行阀角位移等工况参数,从采集的故障工况数据中选取1组作为样本向量,计算该样本向量对样本空间的马氏距离,并进行同样的Box-Cox变换,求得该样本向量的马氏距离为146.374 2。根据正态分布的3σ准则可知,该样本向量已落在(μ+2.58σ, +∞)区域内,即判定此最终执行元件已经发生功能安全失效,与真实测试情况相符。因此, 实际工况条件下进行的测试验证了本文方法的正确性。
4 结束语本文针对现有方法对最终执行元件实际情况有所忽视且没有采用实际参数进行分析的问题,提出一种基于马氏距离的最终执行元件功能安全失效表征方法。该方法利用实际测量所得到的工况参数进行最终执行元件的功能安全失效分析,较之其他方法更具客观性和合理性。仿真实验结果表明该方法能准确识别出3组待测数据的功能安全失效情况;在实际工况条件下该方法对于电磁阀卡堵故障能够进行有效识别,对工业现场在役的无部分行程测试功能的最终执行元件的功能安全可以实现在线检测,解决了最终执行元件功能安全失效的表征问题。
| [1] |
刘太元, 俞曼丽, 郑利军. 安全仪表系统的应用及发展[J]. 中国安全科学学报, 2008, 18(8): 93-100. LIU T Y, YU M L, ZHENG L J. The application and future development of safety instrumented system[J]. China Safety Science Journal, 2008, 18(8): 93-100. (in Chinese) |
| [2] |
靳江红, 吴宗之, 赵寿堂, 等. 安全仪表系统的功能安全国内外发展综述[J]. 化工自动化及仪表, 2010, 37(5): 1-5. JIN J H, WU Z Z, ZHAO S T, et al. Development summarization on functional safety of safety instrumented system[J]. Control and Instruments in Chemical Industry, 2010, 37(5): 1-5. (in Chinese) |
| [3] |
ZHOU Y, ZHU Y P, REN H R, et al. A comprehensive reliability allocation method for CNC lathes based on cubic transformed functions of failure mode and effects analysis[J]. Chinese Journal of Mechanical Engineering, 2015(2): 315-324. |
| [4] |
DUNJÓ J, FTHENAKIS V, VÍLCHEZ J A, et al. Hazard and operability (HAZOP) analysis. A literature review[J]. Journal of Hazardous Materials, 2010, 173(1-3): 19-32. DOI:10.1016/j.jhazmat.2009.08.076 |
| [5] |
夏太武, 袁树海, 宋彬, 等. SIL在天然气净化厂控制系统安全分析中的应用[J]. 天然气工业, 2011, 31(3): 92-96. XIA T W, YUAN S H, SONG B, et al. Application of safety integrity level (SIL) and the hazard and operability analysis (HAZOP) in a natural gas purification plant[J]. Natural Gas Industry, 2011, 31(3): 92-96. (in Chinese) |
| [6] |
MEI J Y, LIU M Z, WANG Y F, et al. Learning a Mahalanobis distance-based dynamic time warping measure for multivariate time series classification[J]. IEEE Transactions on Cybernetics, 2016, 46(6): 1363-1374. DOI:10.1109/TCYB.2015.2426723 |
| [7] |
PATIL N, DAS D, PECHT M. Anomaly detection for IGBTs using Mahalanobis distance[J]. Microelectronics Reliability, 2015, 55(7): 1054-1059. DOI:10.1016/j.microrel.2015.04.001 |








