2. 北京化工大学 信息科学与技术学院, 北京 100029
2. College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China
由于内部输送的腐蚀性介质和外部环境的共同腐蚀作用,油气管道极易发生腐蚀穿孔事故[1]。因此,管道剩余寿命评估成为管道防护工作的重点,是确定管道维护周期和措施的前提[2]。目前,国内外学者常采用神经网络[3]、灰色模型[4]、分形理论[5]等方法确定管道的剩余寿命。在拥有大量数据样本的情况下,神经网络通过建立腐蚀因素与管道腐蚀状态之间的关系,可以准确预测管道的寿命;在缺少数据样本、管道腐蚀因素之间的关系不确定的情况下,常采用灰色模型处理此类问题[6]。在实际应用中,由于灰色模型本身的缺陷,模型预测精度往往不高。为此,研究者们不断提出各种改进办法。骆正山等[7]将背景值优化的无偏等维新息灰色模型和经过白化系数寻优、二次平滑处理的马尔科夫模型相结合建立复合模型,该模型有效地解决了传统模型长期动态预测精度较差的问题。经建芳等[8]采用灰色线性回归模型预测油气管道的腐蚀速率,不仅解决了灰色模型非线性信息处理能力不足的问题,还通过引入误差反向传播算法(BP)进行残差修正,降低了模型的随机误差。
贾宝惠等[9]通过背景值和初始值优化以及引入权重矩阵对不等间距灰色模型进行改进,提出的模型可用于飞机结构件的腐蚀预测。启发式智能优化算法是从自然规律中抽象出的参数求解算法,如粒子群算法(PSO)[10]、蜂群算法(ABC)[11]等,可用于优化灰色模型的生成系数,提高模型的预测精度。
为了改善灰色模型原始序列光滑度和背景值构造公式上的缺陷,使其适用于油气管道的腐蚀预测,本文将指数变换和动态生成系数引入到传统灰色模型中。鉴于ABC算法拥有良好的全局搜索能力,善于求解非线性、多维的复杂问题,采用改进的蜂群算法(IABC)优化模型参数以解决油气管道寿命预测问题。
1 GM(1, 1)模型灰色预测GM(1, 1)模型利用原始序列累加生成新的序列,使原本混乱的数据呈现出规律性,即使只有较少的数据,也能得到良好的预测结果,其一般包括累加生成、建模求解、累减还原3个步骤,具体如下[12]。
1) 累加生成。设X(0)=(x(0)(1), x(0)(2), …, x(0)(n))为原始非负数据序列;则X(1)=(x(1)(1), x(1)(2), …, x(1)(n))为X(0)的一阶累加生成序列,其中
| $ {x^{(1)}}(k) = \sum\limits_{i = 1}^k {{x^{(0)}}} (i) $ | (1) |
式中,k=1, 2, …, n。
则Z(1)=(z(1)(2), z(1)(3), …, z(1)(n))为X(1)的紧邻均值生成序列,其中
| $ {z^{(1)}}(k) = \frac{1}{2}[{x^{(1)}}(k) + {x^{(1)}}(k - 1)] $ | (2) |
式中,k=2, 3, …, n。
2) 建模求解。x(0)(k)+az(1)(k)=b为GM(1, 1)模型的灰微分方程,其白化微分方程为
| $ \frac{{{\rm{d}}{x^{(1)}}(t)}}{{{\rm{d}}t}} + a{x^{(1)}}(t) = b $ | (3) |
式中,a为发展系数,b为灰色作用量,均为待解参数,可通过最小二乘法估计a和b的值
| $ {(a,b)^{\rm{T}}} = {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (4) |
式中,
则白化微分方程的解为
| $ {x^{(1)}}(t) = \frac{b}{a} + \left[ {{x^{(1)}}(1) - \frac{b}{a}} \right]{{\rm{e}}^{ - a(t - 1)}} $ | (5) |
GM(1, 1)模型的时间响应序列为
| $ {\hat x^{(1)}}(k + 1) = \frac{b}{a} + \left[ {{x^{(0)}}(1) - \frac{b}{a}} \right]{{\rm{e}}^{ - ak}} $ | (6) |
式中,k=1, 2, …, n-1。
3) 累减还原。原始数据序列还原值为
| $ {{\hat x}^{(0)}}(k + 1) = {{\hat x}^{(1)}}(k + 1) - {{\hat x}^{(1)}}(k) $ | (7) |
当处理某些光滑度不足的数据序列时,灰色模型的精度会大大下降,常见方法是采用数据变换预处理原始数据以提高其光滑度[13]。本文采用指数函数变换预处理原始数据,建立指数变换灰色模型EGM(1, 1),具体过程如下。
对原始序列作指数变换
| $ {y^{(0)}}(i) = {c^{{x^{(0)}}(k)}},i = k = 1,2, \cdots ,n $ | (8) |
式中,c为底数。按照GM(1, 1)模型对新序列进行建模,得到新的响应序列为
| $ {\hat y^{(1)}}(k + 1) = \frac{b}{a} + \left[ {{y^{(0)}}(1) - \frac{b}{a}} \right]{{\rm{e}}^{ - ak}} $ | (9) |
新序列的还原值为
| $ {{\hat y}^{(0)}}(k + 1) = {{\hat y}^{(1)}}(k + 1) - {{\hat y}^{(1)}}(k) $ | (10) |
由y(0)(k)=cx(0)(k)可得原始序列的还原值为
| $ {{\hat x}^0}(k) = \frac{{\ln {{\hat y}^{(0)}}(k)}}{{\ln c}} $ | (11) |
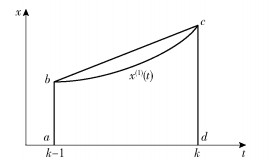
GM(1, 1)模型的背景值构造公式是存在缺陷的,如图 1所示,真实背景值应该是x(1)(t)在[k-1, k]区间上的积分,而传统建模方法的背景值是采用梯形面积作为替代。当处理某些剧烈变化的数据时,传统背景值构造方法会带来较大误差,导致模型的精度下降[14]。
|
图 1 GM(1, 1)模型背景值误差来源 Fig.1 Error sources for the GM(1, 1) model background values |
基于此,本文采用动态生成系数α(i)替代固定值,通过动态调整各区间的生成系数,最大程度降低背景值误差。新的背景值构造公式为
| $ {\hat z^{(1)}}(k) = \alpha (i){x^{(1)}}(k) + (1 - \alpha (i)){x^{(1)}}(k - 1) $ | (12) |
式中,α(i)为动态生成系数,0≤α(i)≤1,i=1, 2, …,n-1, k=2, 3, …,n。
由于求解动态生成系数的参数较多,一般的方法难以求解,而蜂群算法在求解非线性、多维的复杂优化问题时有独特优势,可得到参数的全局最优解,所以采用蜂群算法求解灰色模型的动态生成系数。针对蜂群算法收敛速度低的缺点,引入交叉算子改进蜂群算法的局部搜索方式[15],以提高算法的收敛速度。
ABC算法是一种模仿蜂群采蜜行为寻找问题最优解的启发式智能优化算法,其思想为,整个蜂群有3类蜜蜂,引领蜂负责寻找蜜源并将蜜源的信息传递给跟随蜂;跟随蜂负责按照一定的规则更新蜜源信息;侦查蜂由引领蜂转化而来,负责抛弃陷入局部最优的蜜源,并随机产生一个新的蜜源。算法具体过程如下。
1) 初始化种群 初始化基本参数,根据式(13)随机产生M个蜜源的初始位置,即待优化问题的可行解,并根据式(14)计算各蜜源的初始适应度值fit(i)。
| $ {x_{ij}} = {x_{{\rm{min}},j}} + rand(0,1)({x_{{\rm{max}},j}} - {x_{{\rm{min}},j}}) $ | (13) |
式中,xij为第i个解的j维值;xmin,j, xmax,j为解第j维的下界和上界;i∈{1, 2, …, M}, j∈{1, 2, …D}, D为优化问题解的维度。
| $ fit(i) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{1 + f(i)}},}&{f(i) \ge 0}\\ {1 + |f(i)|,}&{f(i) < 0} \end{array}} \right. $ | (14) |
式中,f(i)为第i个解的目标函数值。
2) 引领蜂阶段 引领蜂根据式(15)在每个蜜源的邻域内进行局部搜索,生成新的蜜源位置vij,并根据式(14)计算新蜜源的fit(i)值。若新蜜源的fit(i)值好于之前的,保留新的蜜源信息并舍弃原先的蜜源信息,反之,保留蜜源信息不变。
| $ {v_{ij}} = {x_{ij}} + {\phi _{ij}}({x_{ij}} - {x_{kj}}) $ | (15) |
式中,k∈{1, 2, …, M},且k≠i;ϕij为[-1, 1]之间的随机数。
3) 跟随蜂阶段 跟随蜂得到引领蜂传递的蜜源信息后,根据式(16)计算每个蜜源被选择的概率pi,然后依据概率选取并更新蜜源信息,更新原则同引领蜂阶段更新方式。
| $ {p_i} = \frac{{fit(i)}}{{\sum\limits_{i = 1}^M {fit(i)} }} $ | (16) |
4) 侦查蜂阶段 若一个蜜源经过多次循环搜索仍没有更新信息,就放弃此蜜源,其对应的引领蜂转变成侦查蜂,并依据式(13)初始化一个新的蜜源。
5) 终止条件判断 判断迭代次数是否超过最大迭代次数,若超过,输出全局最优动态生成系数α(i),否则转向步骤2)循环执行,直至超过最大迭代次数。
ABC算法在更新蜜源时进行随机的邻域搜索[16],没有充分利用当前的最优解,导致算法虽然拥有较强的全局搜索能力,但局部搜索能力较差。为了平衡算法的全局和局部搜索能力,加快算法的收敛速度,引入交叉算子改进搜索策略,用式(17)替代式(15)进行搜索。
| $ {v_{ij}} = \lambda {x_{ij}} + (1 - \lambda )x_{kj}^{{\rm{best}}} $ | (17) |
式中,xkjbest为当前最优解;λ为[0, 1]之间的随机数。
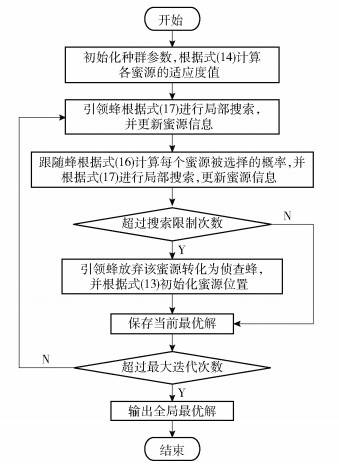
综上所述,IABC算法的具体流程如图 2所示。
|
图 2 改进的蜂群算法流程图 Fig.2 Flow chart of the improved artifitial bee colony algorithm |
为了检验本文提出的预测模型的有效性,引用文献[17]中的常压蒸馏塔塔顶换热器入口分配管弯头测厚数据进行比较分析,壁厚测量的平均值见表 1。表中前12个工作月的数据作为灰色建模方法的原始序列,后6个工作月的数据作为预测序列,用于评估预测方法的准确性。
| 下载CSV 表 1 弯头壁厚值 Table 1 Elbow wall thickness |
本文的目标函数为加权平方误差和,其公式为
| $ \min \sum\limits_{k = 2}^n \varphi (k){\left( {{{\hat x}^{(0)}}(k) - {x^{(0)}}(k)} \right)^2} $ | (18) |
式中,x(0)(k)为建模原始数据序列;
精度检验是衡量模型优劣的重要方法,本文采用灰色绝对关联度和平均相对误差两种检验方法评估模型的精度。
1) 灰色绝对关联度
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{S_0}} \right| = \left| {\sum\limits_{k = 2}^{n - 1} {{x^{(0)}}} (k) + \frac{1}{2}{x^{(0)}}(n)} \right|}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{{\hat S}_0}} \right| = \left| {\sum\limits_{k = 2}^{n - 1} {{{\hat x}^{(0)}}} (k) + \frac{1}{2}{{\hat x}^{(0)}}(n)} \right|}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{{\hat S}_0} - {S_0}} \right| = \left| {\sum\limits_{k = 2}^{n - 1} {\left( {{{\hat x}^{(0)}}(k) - {x^{(0)}}(k)} \right)} + \frac{1}{2}} \right.}\\ {\left. {\left( {{{\hat x}^{(0)}}(n) - {x^{(0)}}(n)} \right)} \right|}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon = \frac{{1 + \left| {{S_0}} \right| + \left| {{{\hat S}_0}} \right|}}{{1 + \left| {{S_0}} \right| + \left| {{{\hat S}_0}} \right| + \left| {{{\hat S}_0} - {S_0}} \right|}}} \end{array} $ | (19) |
式中,S0是原始数据灰色绝对关联计算参数;
2) 平均相对误差δ
| $ \delta = \frac{1}{n}\sum\limits_{k = 1}^n {\left| {\frac{{{{\hat x}^{(0)}}(k) - {x^{(0)}}(k)}}{{{x^{(0)}}(k)}}} \right|} \times 100\% $ | (20) |
当参数设置种群数量N为20,蜜源数量M为10,搜索限制次数limit为20,最大迭代次数maxcycle为50,待优化问题解的维度D为11时,算法可在约20次迭代后收敛。为了保证算法的结果达到最优,算法运行10次,选取误差最小的一次作为最终预测结果。
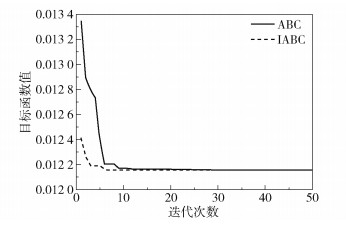
图 3为ABC算法和IABC算法优化灰色模型参数时的收敛情况。从图中可以看出,改进搜索方式后的蜂群算法不但收敛速度明显高于传统的蜂群算法,而且稳定性也得到了一定的提高。
|
图 3 IABC和ABC算法收敛情况 Fig.3 Convergence of IABC and ABC algorithms |
分别基于GM(1, 1)模型、EGM(1, 1)模型和IABC-EGM(1, 1)模型建模,预测结果见表 2。其中GM(1, 1)模型的发展系数a为0.027 6,灰色作用量b为9.153 0;EGM(1, 1)模型的参数(a, b)为(-0.048 8, 0.120 7),底数c为0.791 5;IABC-EGM(1, 1)模型的参数(a, b)为(-0.050 8, 0.119 3),动态生成系数α(i)为(0.370 6, 0.314 7, 0.352 2, 0.604 0, 0.868 0, 0.851 2, 0.550 8, 0.623 3, 0.157 5, 0.215 4, 0.019 6)。从表 2可知,相比于GM(1, 1)模型,改进后的两种模型在整体上预测精度得到一定提高。
| 下载CSV 表 2 弯头壁厚预测值 Table 2 Predicted values of the elbow wall thickness |
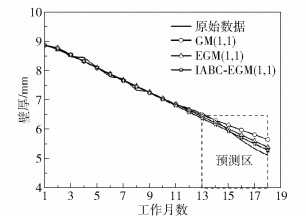
图 4、图 5分别为3种模型的预测值和相对误差对比。从图中可知,除了在13和14两个工作月中,IABC-EGM(1, 1)模型和EGM(1, 1)模型的预测误差略大于GM(1, 1)模型外,它们于15~18个工作月的预测结果均优于GM(1, 1)模型,并且IABC-EGM(1, 1)模型的最小相对误差为0.005 3,最大相对误差为0.033 5,误差波动相比于GM(1, 1)模型更小,中长期的预测结果精度更高。可见,利用指数变换预处理原始数据序列和动态生成系数重构背景值公式的方法是有效的,改进后的模型不仅能处理剧烈变化的数据序列,还能处理光滑度不足的数据序列,弥补了GM(1, 1)模型的缺陷。
|
图 4 预测值对比 Fig.4 Comparison of predicted values |

|
图 5 相对误差对比 Fig.5 Comparison of relative errors |
表 3为3种模型预测结果的平均相对误差和灰色绝对关联度对比。从表 3可知,IABC-EGM(1, 1) 模型的平均相对误差比GM(1, 1)模型降低了2.64%,灰色绝对关联度提高了0.02。可见,IABC-EGM(1, 1)模型的预测精度更高,能更好地预测油气管道的腐蚀程度。
| 下载CSV 表 3 模型精度对比 Table 3 Comparison of model accuracy |
(1) 针对GM(1, 1)模型预测管道壁厚变化时精度较低的问题,从原始序列光滑度和背景值构造公式两方面入手,采用指数变换和动态生成系数改进模型的建模过程,并引入IABC算法求解参数,实现了对管道壁厚值的准确预测。
(2) 相比于GM(1, 1)模型,IABC-EGM(1, 1)模型的平均相对误差降低了2.64%,灰色绝对关联度提高了0.02,预测结果更加接近真实值。在缺少大量腐蚀数据时,可采用本文提出的模型预测油气管道重点腐蚀部位的壁厚变化趋势,并根据管道的最大允许腐蚀深度计算剩余寿命。
(3) IABC-EGM(1, 1)模型壁厚预测值的相对误差均小于4%,达到5%的二级精度等级标准,可为油气管道的腐蚀防护提供数据参考。
| [1] |
黄坤, 吴佳丽, 全恺, 等. 含腐蚀缺陷油气管道评价技术研究进展[J]. 表面技术, 2018, 47(1): 116-122. HUANG K, WU J L, QUAN K, et al. A review on evaluation technology of oil-gas pipelines with corrosion defect[J]. Surface Technology, 2018, 47(1): 116-122. (in Chinese) |
| [2] |
翁官锐. 油气长输管道剩余寿命预测综述[J]. 广州化工, 2015, 43(23): 62-64. WENG G R. Review of residual life prediction for long-distance transportation oil & gas pipeline[J]. Guangzhou Chemical Industry, 2015, 43(23): 62-64. (in Chinese) |
| [3] |
OBASEKI M. Diagnostic and prognostic analysis of oil and gas pipeline with allowable corrosion rate in Niger Delta Area, Nigeria[J]. Journal of Applied Sciences and Environmental Management, 2019, 23(5): 927-934. DOI:10.4314/jasem.v23i5.24 |
| [4] |
LI G D, WANG C H, YAMAGUCHI D, et al. A study on the corrosion process of gas pipeline applying grey dynamic model[J]. International Journal of Reliability and Safety, 2010, 4(1): 1-15. DOI:10.1504/IJRS.2010.029562 |
| [5] |
陈永红, 张大发, 王悦民, 等. 基于分形理论的核动力管道腐蚀坑深度预测模型研究[J]. 原子能科学技术, 2009, 43(8): 673-677. CHEN Y H, ZHANG D F, WANG Y M, et al. Corrosion pit depth prediction model of nuclear power pipeline using fractal theory[J]. Atomic Energy Science and Technology, 2009, 43(8): 673-677. (in Chinese) |
| [6] |
姜峰, 郑运虎. 预测腐蚀管道剩余寿命的新方法研究[J]. 机械强度, 2015, 37(3): 539-545. JIANG F, ZHENG Y H. Study of a new method for the remaining life prediction of corrosion pipeline[J]. Journal of Mechanical Strength, 2015, 37(3): 539-545. (in Chinese) |
| [7] |
骆正山, 陈晨, 王哲. 优化的Gray Markov模型在埋地管道腐蚀速率预测中的应用[J]. 腐蚀与防护, 2019, 40(5): 313-317, 326. LUO Z S, CHEN C, WANG Z. Application of improved Gray Markov model in predicting corrosion rate of oil and gas pipelines[J]. Corrosion & Protection, 2019, 40(5): 313-317, 326. (in Chinese) |
| [8] |
经建芳, 李康春, 邓富康, 等. 油气管道腐蚀的灰色线性回归组合预测模型[J]. 油气储运, 2015, 34(12): 1300-1304. JING J F, LI K C, DENG F K, et al. Prediction model of oil and gas pipeline corrosion based on grey-linear regression combination[J]. Oil & Gas Storage and Transportation, 2015, 34(12): 1300-1304. (in Chinese) |
| [9] |
贾宝惠, 张博, 王毅强. 基于改进不等时距灰色模型的老龄飞机结构腐蚀预测[J]. 腐蚀与防护, 2019, 40(3): 205-208. JIA B H, ZHANG B, WANG Y Q. Structural corrosion prediction of aging aircraft based on improved unequal interval grey model[J]. Corrosion & Protection, 2019, 40(3): 205-208. (in Chinese) |
| [10] |
LI C M, GAO H M, QIU J L, et al. Grey model optimized by particle swarm optimization for data analysis and application of multi-sensors[J]. Sensors, 2018, 18(8): 2503. DOI:10.3390/s18082503 |
| [11] |
GAO H, SHI Y J, PUN C M, et al. An improved artificial bee colony algorithm with its application[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 1853-1865. DOI:10.1109/TII.2018.2857198 |
| [12] |
罗党, 刘思峰, 党耀国. 灰色模型GM(1, 1)优化[J]. 中国工程科学, 2003, 5(8): 50-53. LUO D, LIU S F, DANG Y G. The optimization of grey model GM (1, 1)[J]. Engineering Science, 2003, 5(8): 50-53. (in Chinese) |
| [13] |
边国兴, 徐亚明. 基于数据变换的GM(1, 1)模型改进[J]. 测绘地理信息, 2019, 44(4): 122-124. BIAN G X, XU Y M. Improvement of GM (1, 1) model based on data transformation[J]. Journal of Geomatics, 2019, 44(4): 122-124. (in Chinese) |
| [14] |
马萍. 灰色系统GM(1, 1)模型的改进及灰色统计模型研究[D]. 长春: 吉林大学, 2007. MA P. Improvement to GM(1, 1) model and research on grey statistical models[D]. Changchun: Jilin University, 2007. (in Chinese) |
| [15] |
王伟, 龙文. 基于交叉算子的改进人工蜂群算法[J]. 兰州理工大学学报, 2015, 41(1): 101-106. WANG W, LONG W. Modified artificial bee colony algorithm based on crossover operators[J]. Journal of Lanzhou University of Technology, 2015, 41(1): 101-106. (in Chinese) |
| [16] |
林凯, 陈国初, 张鑫. 多交互式人工蜂群算法及其收敛性分析[J]. 计算机应用, 2017, 37(3): 760-765. LIN K, CHEN G C, ZHANG X. Multiple interactive artificial bee colony algorithm and its convergence analysis[J]. Journal of Computer Applications, 2017, 37(3): 760-765. (in Chinese) |
| [17] |
王正方, 王勇, 刘秀华. 基于灰色系统理论的常压蒸馏装置腐蚀预测[J]. 中国石油大学学报(自然科学版), 2010, 34(2): 114-118. WANG Z F, WANG Y, LIU X H. Grey system prediction of corrosion on oil atmospheric distillation equipment[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010, 34(2): 114-118. (in Chinese) |








