2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室, 北京 100029
2. Beijing Key Laboratory of Health Monitoring and Self-recovery for High-end Mechanical Equipment, Beijing University of Chemical Technology, Beijing 100029, China
旋转机械振动故障中有70%以上的故障是由转子系统的质量不平衡造成的[1-5],通常采用多次启停车、试重、配重等工序进行转子系统的动平衡[6-7]。自动平衡技术可在线实时改变既定平面上配重块位置产生振动的补偿矢量,具有无需停车就可配重的显著优点[8-13],在工业领域得到越来越多的关注及应用,例如民用的高精度机床、磨床以及军用涡桨螺旋桨自动平衡系统等。国外自20世纪90年代起针对自动平衡技术开展研究,美国Lord公司、空客公司等多家企业已取得一系列自动平衡专利并已投入实际应用[14-17],国内研究则起步较晚,至今尚无工业实际应用的报道。
自动平衡装置以其作用力产生方式的不同可分为加重/去重式、外加作用力式和改变质量分布式等3种类型[18]。其中,加重/去重式自动平衡装置主要是通过激光或喷涂等方式直接改变转子的质量及其分布,平衡过程中产生的金属微粒会对环境造成污染,且会在转子表面形成伤痕,降低转子的寿命;外加作用力式一般是通过电磁轴承对转子持续施加一个与转子不平衡量等大反向的作用力,强行将转子的质心拉至与旋转中心重合,但所需能耗较大,且需对转子的转速进行持续精确的跟踪以使作用力与转子保持同步旋转,控制难度大;改变质量分布式主要是通过在转子上安装质量分布可调的装置,通过装置内配重块的位置改变来调整转子系统的质量分布,以达到降低不平衡振动的目的,这种方式占用空间小且附加装置少,应用较为广泛。
以电磁式自动平衡为例[2],通过预装在转子上的两个可相对转动的配重块合成补偿矢量,相比于激光加重/去重型平衡装置,其结构简单,控制方便,不会产生污染和疲劳损伤问题,然而需在平衡过程中精确定位两个配重块在圆周上的位置以获得准确的补偿矢量,自动配平补偿矢量的精度会直接影响平衡效果,如果定位监测误差过大,将产生错调、超调,甚至造成平衡失败。因此,本文提出一种基于可编程逻辑控制器(PLC)高速采集模块的自动平衡配重块位置精确测算方法,一方面从硬件系统上脱离对计算机和高速数采设备的依赖,大大提高了控制系统的稳定性和灵活性,有利于实现自动平衡系统的轻量化设计;另一方面从检测算法上实现了对自动配平补偿矢量的精稳测算。
1 自动配平矢量测算原理 1.1 自动平衡系统结构电磁式自动平衡头的结构分为动环和静环两部分,其三维结构示意图如图 1所示。动环安装在旋转轴上随轴一起旋转,静环通过支架固定在底座上。动环两个配重盘的特定半径处分别安装有一个具有一定质量的配重块,在转子旋转过程中,每个配重块会产生一个补偿平衡矢量,两个配重块的相对位置不同即可产生不同大小和方向的合补偿平衡矢量。配重盘外沿安装有一圈相邻且极性相反的永磁体,可根据需要与静环产生的电磁力发生相互作用进而驱动配重块移动。配重块位于指定位置时,其位置由永磁体形成的自锁力锁定。在动环端盖和两个配重块的外沿上各安装有一个定位磁铁,用于配重盘位置的实时监测。在静环的对应位置上使用3个霍尔传感器分别检测基准磁铁和两个配重块定位磁铁的信号,3个霍尔传感器在轴向方向上布置成一条直线且与转子轴线平行。静环的主体是电磁线圈,对线圈通电可在动静环之间形成一个电磁场,按一定规律变化的电磁场与配重盘上永磁体的磁场相互作用使配重块与轴发生相对转动,配重块的目标位置由转动的方向和步数指定。

|
图 1 自动平衡头结构示意图 Fig.1 Schematic diagram of the automatic balance head |
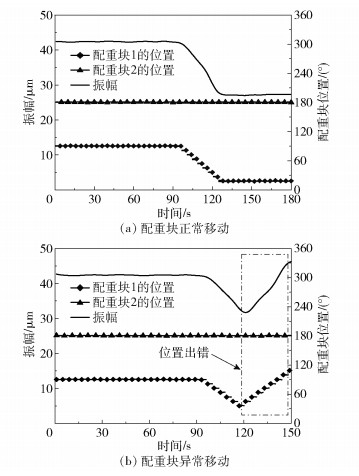
振动传感器实时监测转子的振动状况,当监测到转子的振动值超过设定的振动阈值时,控制系统根据测量到的数据计算质量不平衡量的大小和相位,自动平衡头经过无错调算法计算配重盘的目标位置并选择最佳移动路径,使两个配重块所产生的合补偿矢量与转子系统原有的质量不平衡矢量方向相反,大小相等,以实现不平衡振动的实时抑制[19]。若转子振动值超过平衡头的平衡能力,则控制系统会驱动平衡头产生最大补偿矢量并同时提示报警信息,通知操作人员及时停机检修。配重块正常移动时平衡头的振动抑制效果如图 2(a)所示,若在配重块移动过程中对其位置发生误判则将导致配重块反向移动,振动增大,如图 2(b)所示。
|
图 2 自动平衡头振动抑制效果示意图 Fig.2 Schematic diagram of the vibration suppression effect of the automatic balance head |
为了精确合成所需的合补偿平衡矢量,必须精准定位配重块的当前位置,保证配重盘移动的准确性。目前使用的高速旋转机械的自动平衡装置多采用高速数据采集设备实现内部配重盘的定位信号采集,但是高速数据采集设备通常需要配备计算机软件和硬件才能实现相应的采集和计算功能,然而实际使用中,在工业现场或航空发动机上往往无法加载太多设备。因此,设计一种工作时不依赖于计算机的定位信号采集系统非常有必要。
1.2 测算原理通常采用高速数据采集设备(如NI高速采集器)搭配上位机采集软件(如LabVIEW软件)进行高速脉冲信号的检测与分析,该设备必须依赖计算机和上位机的采集软件,灵敏度较高,但在实际的复杂电磁环境和工业环境下应用极易受到干扰,具有一定的局限性,且价格昂贵。PLC是一种专门为在工业环境下应用而设计的控制系统,具有可靠性高、编程容易、安装方便、组态灵活、抗干扰能力强等优点,与触摸屏等设备配合使用可以脱离对计算机的依赖。将配重块定位模块和执行器驱动模块整合到同一设备中,可有效降低数据传递过程造成的时延。因此,本文计划开发一种基于PLC的低成本、高稳定性、操作简单且可脱离计算机独立运行的配重块定位检测系统。
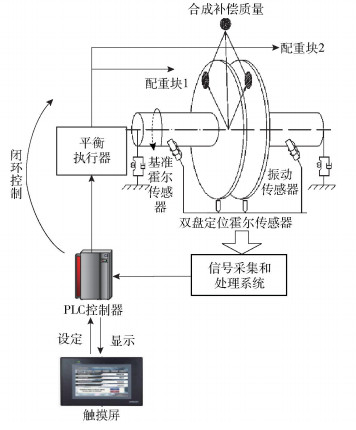
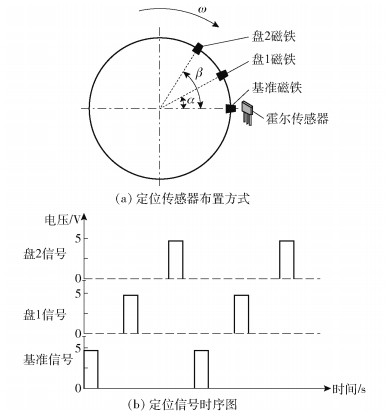
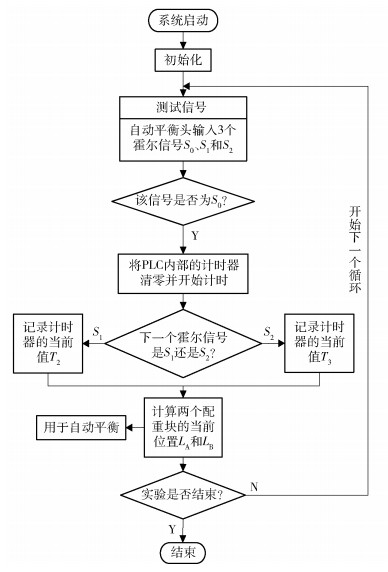
配重块定位检测与控制系统组成如图 3所示,基准霍尔传感器和双盘定位霍尔传感器分别采集3个磁铁的信号,计算出两个配重块在平衡头上的相对位置后反馈给PLC控制器和平衡执行器,形成闭环控制。配重块定位传感器布置方式和信号时序如图 4所示,位置计算过程如图 5所示,根据双盘定位信号在转子旋转周期中出现的位置即可计算出两盘的位置。
|
图 3 配重块定位检测与控制系统 Fig.3 Position detection and control system of the counterweight |
|
图 4 配重块位置检测方式 Fig.4 Principle of the position detection of the counterweight |
|
图 5 配重块位置计算流程图 Fig.5 Flow chart of the counterweight position calculation |
实际试验中使用的自动平衡头的配重块旋转一周共有80步,步距角为4.5°。在自动平衡头配重块的定位检测中,计算得到的配重块位置的稳定性非常重要,即使有一步的波动也会导致配重块移动的混乱,使平衡头达不到理想的平衡效果,甚至会增大轴的振动,危及工作人员的生命及财产安全,因此要求两个配重块位置检测结果必须稳定,配重块位置计算结果误差不能超过1步。
2 补偿矢量的测算方法 2.1 计时法基准磁铁经过对应的霍尔传感器时产生一个脉冲信号,启动PLC内部的计时器开始计时,计时器初始值为0,当基准磁铁再次经过霍尔传感器时计时器的当前值为T1,即转子旋转一圈所用的时间为T1,所以转子的转速
| $ v=\frac{60}{T_{1}} $ | (1) |
在转子旋转一圈的过程中,另外两个霍尔传感器接收到对应磁铁的信号,并同时记录计时器的当前值T2和T3,则两个配重块A和B的当前位置分别为
| $ {L_{\rm{A}}} = \frac{{{T_2}}}{{{T_1}}} \times 80,{L_{\rm{B}}} = \frac{{{T_3}}}{{{T_1}}} \times 80 $ | (2) |
准确计算位置结果的关键在于T1、T2、T3的精确测量。但由于使用PLC的高速脉冲功能即可达到所需的定位精度,且有助于简化测控系统整体的复杂程度,因此不采用高速数据采集设备对时间进行更高精度的测量。
2.2 脉冲计数法PLC可稳定地产生指定频率的高速脉冲,设脉冲频率为f,转子旋转一圈对应的脉冲个数为n,基准信号到两个配重块霍尔信号之间包含的脉冲个数为n1和n2,则转速
| $ v = \frac{{60 \times f}}{n} $ | (3) |
两个配重块的当前位置为
| $ L_{\rm{A}}^\prime = \frac{{{n_1}}}{n} \times 80,L_{\rm{B}}^\prime = \frac{{{n_2}}}{n} \times 80 $ | (4) |
在实际试验中,脉冲数的采集不可避免地会受到外界因素的干扰,其中最主要的是转子转速的波动产生的角加速度与转子振动所引起的额外力和力矩在配重盘平面内的分量,因此必须考虑这些干扰对配重块位置计算的影响。设无外界扰动时两个配重盘的位置分别为L′A1和L′B1,当外界扰动使得n1和n2产生一个大小为Δn的波动时,两个配重盘的位置分别为L′A2和L′B2,则两个配重块的计算位置产生的误差为
| $ \begin{array}{*{20}{c}} {\frac{{L_{{\rm{A}}2}^\prime - L_{{\rm{Al}}}^\prime }}{{L_{{\rm{A}}1}^\prime }} = \frac{{\frac{{{n_1} + \Delta n}}{n} \times 80 - \frac{{{n_1}}}{n} \times 80}}{{\frac{{{n_1}}}{n} \times 80}} = \frac{{\Delta n}}{{{n_1}}},}\\ {\frac{{L_{{\rm{B}}2}^\prime - L_{{\rm{B}}1}^\prime }}{{L_{{\rm{B}}1}^\prime }} = \frac{{\frac{{{n_2} + \Delta n}}{n} \times 80 - \frac{{{n_2}}}{n} \times 80}}{{\frac{{{n_2}}}{n} \times 80}} = \frac{{\Delta n}}{{{n_2}}}} \end{array} $ | (5) |
所以n1和n2的大小与脉冲频率f有关。由此可以看出提高脉冲的频率有利于减小随机误差,但是过高的脉冲频率也更容易受到噪声干扰,稳定性降低,因此脉冲频率不宜过高。
2.3 优化的脉冲计数法转子旋转过程中传感器信号会因环境因素的干扰而产生随机的波动,由最小二乘法的回归方程
| $ \left\{ {\begin{array}{*{20}{l}} {a = \frac{{\sum x y - \frac{1}{N}\sum x \sum y }}{{\sum {{x^2}} - \frac{1}{N}{{\left( {\sum x } \right)}^2}}}}\\ {b = \bar y - a\bar x} \end{array}} \right. $ | (6) |
可知一组数据的回归拟合曲线必经过平均值点(x, y)。若每次平均的数据量为n,当其中有x(x < n/2) 个直接位置计算结果产生了总量为Δn的误差时,平均后的相对误差为
| $ \frac{{\Delta n}}{n} < \frac{{\Delta n}}{x} \times \frac{1}{2} $ | (7) |
即平均后每个直接位置计算结果产生误差的影响小于平均前每个直接位置结果平均误差的一半,当平均前每个直接位置结果的平均误差为4.5°时,平均后每个直接位置计算结果产生的误差小于2.25°,所以平均化处理可以将误差缩小至允许范围内。为消除环境干扰带来的误差,在高速脉冲定位的基础上对一段时间内的数据进行取平均值运算,将角度计算的波动值降低至±2.25°以下,达到使定位结果稳定的目的。
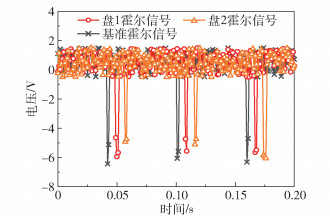
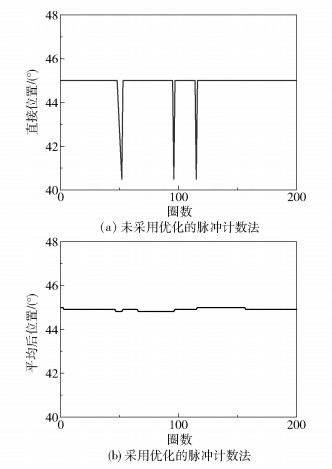
3 试验验证 3.1 测算方法仿真实际试验中使用的自动平衡头的步距角为4.5°,采用LabVIEW模拟其基准霍尔信号和双盘的霍尔信号,计算两个配重盘的当前位置,并进行仿真定位试验,得到的模拟信号如图 6所示,图中每个突出的尖峰代表一个霍尔信号,所有模拟信号均为仅相位不同的方波和同一个白噪声的叠加,与实际霍尔信号相似。以盘1为例,当盘1的角度计算值上下波动超过步距角的一半,即误差超过±2.25°时,其位置计算结果与实际位置就会产生1步的误差。仿真试验中盘1信号和基准信号的相位差为45°,对应盘1的第10步位置,仿真结果如图 7(a)所示。由仿真结果可知采用脉冲计数的计算方式在仿真的200圈内产生了3次计算位置从45°到40.5°的突变,盘1计算位置偏离实际位置,位置计算结果不够稳定,应对此方案进行改进。
|
图 6 配重盘定位仿真信号 Fig.6 Simulation signal of counterweight positioning |
|
图 7 仿真试验结果 Fig.7 Simulation test results |
转子旋转过程中传感器信号会受到很多因素的干扰而产生随机波动,进而导致定位产生误差。为了消除波动带来的误差,对盘1位置仿真的数据进行平均化处理,即每次盘1的计算位置取相邻的50个直接位置计算结果的平均值作为本次的盘1位置,所得结果如图 7(b)所示,平均后的角度计算结果的波动未超过±2.25°,盘1的位置计算结果稳定在45°位置,表明此方案配重盘定位稳定准确。
3.2 螺旋桨自动平衡试验台测试以欧姆龙公司的CP1H PLC作为控制系统核心设备,螺旋桨自动平衡试验台如图 8所示,基于PLC进行配重块定位检测计算的流程如图 5所示。

|
图 8 螺旋桨自动平衡试验台 Fig.8 View of the propeller automatic balance test bench |
根据定位精度要求,配重块的位置采集应至少达到可分辨80个稳定位置及相邻两个稳定位置的中间位置的分辨率,即总共160个位置。试验台的工作转速为1 200 r/min,也即20 r/s,由采样定理可知,采样频率应至少为分析频率的2倍,本试验中取5倍,所以脉冲频率的下限为
| $ {f_{{\rm{s}},\min }} = 160 \times 20 \times 5 = 16 \times {10^3}{\rm{Hz}} $ | (8) |
根据试验要求和试验条件对脉冲频率进行向上取整,最终脉冲频率设定为20 kHz。
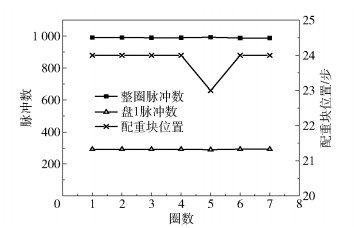
在某次实际试验中将配重块1固定于第24步的位置上,表 1为某时间段内的脉冲个数,对应的位置计算结果如图 9所示。其中第4圈总脉冲数为990个,配重块1所对应的脉冲数为292个,则配重块1位置
| 下载CSV 表 1 脉冲计数法试验数据 Table 1 Experimental data for the pulse counting method |
|
图 9 脉冲计数法位置结果 Fig.9 Position results for the pulse counting method |
| $ L_{\mathrm{A} 1}=\frac{T_{2}}{T_{1}} \times 80=\frac{292}{990} \times 80=23.596(\text { 步 }) $ | (9) |
因为步数必为整数,所以将上述计算结果四舍五入得到当前位置为第24步,然而第五圈总脉冲数为993个,配重块1所对应的脉冲数为290个,则配重块1位置
| $ L_{\mathrm{A} 2}=\frac{T_{2}}{T_{1}} \times 80=\frac{290}{993} \times 80=23.364(\text { 步 }) $ | (10) |
四舍五入后得到当前位置为第23步,与上一圈的位置计算结果错位1步,不满足计算结果误差必须小于1步的精度要求。
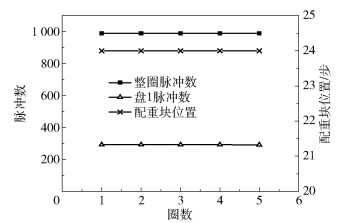
对连续多圈的脉冲数据取平均值,消除偶然产生的计算位置的波动。对脉冲计数方案的试验数据进行分析后发现,配重块位置的波动主要是由外界扰动导致脉冲数目的波动引起的,当基准霍尔传感器和配重盘霍尔传感器截取到的脉冲数目同时产生某种波动的组合时,计算出的配重块位置就会产生波动。经反复试验发现对连续的50组数据求平均可使配重块的位置检测结果完全稳定,达到所需的定位精度。表 2为平均化后计算出的配重块1位置的部分数据,对应的位置计算结果如图 10所示,可以看出配重块位置计算结果稳定。
| 下载CSV 表 2 优化脉冲计数法试验数据 Table 2 Experimental data for the optimized pulse counting method |
|
图 10 优化脉冲计数法位置结果 Fig.10 Position results for the optimized pulse counting method |
(1) 基于PLC的自动平衡配重块定位检测系统,可脱离对计算机和高速数采设备的依赖,简化控制系统结构和各模块间数据交换流程,降低了不同元件间通讯受干扰发生错误的概率。
(2) 基于PLC的自动平衡配重块定位检测系统,实现了定位监测和驱动控制的测控一体,有利于实现自动平衡系统轻量化设计,提高控制系统稳定性,同时也降低了控制系统成本,具有潜在的工业应用价值。
(3) 基于PLC的自动平衡配重块定位检测系统,消除了配重块位置由高速数采设备到计算机再到PLC的数据采集、处理和传递过程中存在的时延,提高了系统的响应速度,为进一步实现振动的快速响应和抑制提供了一定的基础。
鉴于PLC良好的电磁兼容性能,在后续研究中需考虑将振动监测纳入定位检测程序,进一步提高自动平衡控制系统的集成度。此外,本文仅针对实验室工况进行了测试方案的原理性验证,后继需结合实际工作环境(如存在交变电磁场的工作环境、非稳态工作转速等)逐步完善抗干扰硬件配置和测试方案。
| [1] |
曹晰, 陈立芳, 高金吉. 用于转子自动平衡的双盘电磁型平衡头移动控制方法研究[J]. 北京化工大学学报(自然科学版), 2010, 37(4): 121-125. CAO X, CHEN L F, GAO J J. Study of bi-disc electro-magnetic balancer movement control for rotor auto-balancing[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2010, 37(4): 121-125. (in Chinese) |
| [2] |
陈立芳, 吴海琦, 王维民, 等. 双配重平衡头无错调控制算法研究[J]. 北京化工大学学报(自然科学版), 2012, 39(2): 89-94. CHEN L F, WU H Q, WANG W M, et al. A study of an error-free movement control algorithm for a bi-disc balancer[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2012, 39(2): 89-94. (in Chinese) |
| [3] |
陈长征, 罗跃纲. 风机现场动平衡研究[J]. 风机技术, 2001(5): 22-23, 40. CHEN C Z, LUO Y G. Research of fan dynamic balance on site[J]. Chinese Journal of Turbomachinery, 2001(5): 22-23, 40. (in Chinese) |
| [4] |
丛培田, 李秀刚. 单面现场动平衡解析三点加重法试验研究[J]. 风机技术, 2001(6): 36-37. CONG P T, LI X G. A study of three point add mass method for single plane field balance[J]. Chinese Journal of Turbomachinery, 2001(6): 36-37. (in Chinese) |
| [5] |
何青, 杜冬梅, 杨昆. 风机振动的在线监测与动平衡[J]. 风机技术, 2001(6): 57-60. HE Q, DU D M, YANG K. On-line monitoring & dynamic balance of vibration on fan[J]. Chinese Journal of Turbomachinery, 2001(6): 57-60. (in Chinese) |
| [6] |
刘占辉, 罗剑斌, 卢一兵. 影响系数法在引风机现场动平衡中的应用[J]. 风机技术, 2011(3): 79-82. LIU Z H, LUO J B, LU Y B. Application of influence coefficient method in field dynamic balance of wind fan[J]. Chinese Journal of Turbomachinery, 2011(3): 79-82. (in Chinese) |
| [7] |
施俊侠, 王大成, 黄斌. 离心式压缩机的振动故障分析[J]. 风机技术, 2003(6): 47-49. SHI J X, WANG D C, HUANG B. Vibration fault analysis of centrifugal compressor[J]. Chinese Journal of Turbomachinery, 2003(6): 47-49. (in Chinese) |
| [8] |
罗轶超. 基于振动信号提取的转子主动平衡[D]. 合肥: 合肥工业大学, 2015. LUO Y C. Active balancing technology of rotor based on unbalanced vibration signal extraction[D]. Hefei: Hefei University of Technology, 2015. (in Chinese) |
| [9] |
樊红卫, 智静娟, 史必佳, 等. 转子自适应主动平衡算法及电磁平衡头单盘平衡试验[J]. 西安交通大学学报, 2018, 52(8): 15-21, 29. FAN H W, ZHI J J, SHI B J, et al. Adaptive rotor balancing algorithm and single-disk rotation test for electromagnetic balancer[J]. Journal of Xi'an Jiaotong University, 2018, 52(8): 15-21, 29. (in Chinese) |
| [10] |
BADRE-ALAM A, BOSWELL D, MORRIS D, et al. Aircraft propeller balancing system: US 8961140B2[P]. 2015-02-24.
|
| [11] |
HILDEBRAND S F, ALTIERI R E, WINZENZ W. Aircraft with transient-discriminating propeller balancing system: US 8360728B2[P]. 2013-01-29.
|
| [12] |
LU C J, TIEN M H. Pure-rotary periodic motions of a planar two-ball auto-balancer system[J]. Mechanical Systems and Signal Processing, 2012, 32: 251-268. DOI:10.1016/j.ymssp.2012.06.001 |
| [13] |
PERKINSON R H, DANIELSON D R. Simplified propeller balancing system and method: US 9512728B2[P]. 2016-12-06.
|
| [14] |
DYER S W, KERLIN J, HACKETT B K. Eletromagnet-ically actuated rotating machine unbalance compensator: US 5757662A[P]. 1998-05-26.
|
| [15] |
WELSH W A. Dual frequency hub mounted vibration suppressor system: US 8403643B2[P]. 2013-03-26.
|
| [16] |
WINZENZ W, BOSWELL D, BADRE-ALAM A, et al. Aircraft propeller balancing system: EP 2647567A2[P]. 2013-09-10.
|
| [17] |
ESTEBAN Q H. Method for balancing a propulsive system having non-hull contra-rotating propellers: US 8998580B2[P]. 2015-04-07.
|
| [18] |
陈哲超. 基于PLC的自动平衡控制系统及方法研究[D]. 北京: 北京化工大学, 2018. CHEN Z C. Research on automatic balancing control system and method for turboprop engine based on PLC[D]. Beijing: Beijing University of Chemical Technology, 2018. (in Chinese) |
| [19] |
PAN X, WU H Q, GAO J J, et al. New liquid transfer active balancing system using compressed air for grinding machine[J]. Journal of Vibration and Acoustics, 2015, 137(1): 011014. DOI:10.1115/1.4028507 |







