2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室, 北京 100029;
3. 中国船舶工业综合技术经济研究院, 北京 100081
2. Beijing Key Laboratory for Health Monitoring and Self-recovery of High-end Mechanical Equipment, Beijing University of Chemical Technology, Beijing 100029;
3. China Shipbuilding Industry Institute of Comprehensive Technology and Economy, Beijing 100081, China
滚动轴承是旋转机械中最为关键的部件之一,针对其进行状态监测及故障诊断对于维护设备的安全运行具有重大意义[1-3]。目前针对轴承的状态监测及故障诊断技术主要以振动监测及温度监测为主。近年来,声音信号在轴承故障诊断领域的应用备受关注[4]。基于声音信号的测量与分析实现设备状态监测及故障诊断的分析方法被称为声学诊断技术(acoustical-based diagnosis, ABD)[5]。振动及温度等接触式测量传感器采集所得信号受外界干扰较小,信号稳定性强,但在高温、高压、高腐蚀等恶劣环境下传感器安装较为困难。声信号测量相比于接触式测量具有无需黏附传感器、测量方便灵活且不影响设备正常工作等优点[6],但声信号测量受环境影响较大,信号成分复杂且信噪比较低,一定程度上限制了声学诊断技术的应用。
近年来,国内外学者针对轴承的声信号监测及诊断技术研究取得了较多研究成果。Amarnath等[7]提出一种将经验模态分解(empirical mode decomposition,EMD)应用于轴承故障诊断的声信号处理方法,但该方法并未结合轴承声信号受环境噪声干扰较大的特点对EMD算法进行改进,在复杂声场条件下诊断结果准确率较低。Law等[8]将小波分析与希尔伯特-黄变换相结合对轴承声信号进行分析,解决了EMD的模态混叠问题,但在复杂声场环境下运算量较大,无法在实际工程测量环境中实现有效应用。周俊等[9]提出一种将盲解卷积、形态滤波和频域压缩感知重构的稀疏分量分析相结合的故障声学诊断方法,用来提取滚动轴承的故障特征,但该方法针对实际测量环境与信号特点设置参数较多,在复杂多变的环境噪声干扰下诊断结果的准确率较低。鲁文波等[10]结合近场声全息技术与灰度共生矩阵提取滚动轴承声场分布特征,但该方法仅可适用于近场条件,在工程上采用远场测量的应用前提下,诊断结果受噪声干扰较大。
共振稀疏分解算法是一种建立在可调品质因子小波变换基础上、可以有效提高信号冲击特性的降噪方法。Selesnick[11]提出信号共振稀疏分解算法,依据信号持续震荡成分及瞬态冲击成分品质因子的不同,将信号分解为持续震荡成分组成的高共振分量及瞬态冲击成分组成的低共振分量。王新华等[12]提出一种结合共振稀疏分解与偏置单稳随机共振的方法,剔除了部分干扰信号,可对管道损伤进行有效评估。孙云嵩等[13]提出一种基于共振稀疏分解的阶比分析方法提取齿轮振动冲击信号,但该方法仅适用于转速波动下的非平稳信号,适用范围有限。陈保家等[14]采用品质因子优化和子带重构的共振稀疏分解算法提取轴承的振动冲击特性,但该算法无法直接应用于轴承的声信号处理,适用性较差。
综上所述,目前针对于轴承的声信号处理算法在复杂声场环境下无法快速有效地提取信号的冲击特性,受环境干扰诊断结果准确率较低。声音传感器采集所得信号中,除故障轴承振动产生的声信号外,还包含设备运行与空气间相互作用产生的信号、现场施工信号、设备其他部件振动引起的信号以及人员交流声音等环境声信号。同时声信号传递路径较为复杂、空间范围内反射次数较多且信号衰减明显,进一步降低了信号质量,信号信噪比较低。本文针对声信号的以上特点,提出一种结合共振稀疏分解及冗余第二代小波包去噪的声学诊断方法,增强了子带的冲击特性,实现了基于声信号的轴承故障诊断。最后通过故障模拟实验对本文方法的可行性进行了验证。
1 信号降噪理论 1.1 共振稀疏分解算法目前对于滚动轴承的故障诊断常采用频率分析与滤波相结合的方法对轴承信号进行分析,然而时频分析法并不能直接适用于所有信号,它们在本质上仅能对振荡或周期性信号进行有效分析[15]。
共振稀疏分解算法可将复杂信号x分解成由持续振荡成分组成的高共振分量x1和由瞬态冲击成分组成的低共振分量x2,原始信号由上述两部分线性叠加而成。采用双通道分解滤波器组对采集所得轴承声信号进行可调品质因子小波变换,求取高Q变换与低Q变换基函数库,其方法原理如图 1所示[16-17]。
图 1中,H0(ω)及H1(ω)分别代表低通和高通滤波器,v0(n)和v1(n)为滤波后子带信号,α和β分别代表低通、高通尺度因子。品质因子Q、冗余因子r、最大分解层数Lmax可参考式(1)~(3)进行设置[18]。
| $ {Q = \frac{{2 - \beta }}{\beta }} $ | (1) |
| $ {r = \frac{\beta }{{1 - \alpha }}} $ | (2) |
| $ {{L_{\max }} \le \frac{{\lg (\beta N/8)}}{{\lg (1/\alpha )}}} $ | (3) |

|
图 1 双通道分解滤波器组 Fig.1 Double-channel decomposition filter banks |
品质因子Q的数值大小表征了信号共振属性的高低,通常设置为1~9之间的整数,信号分解所得高、低共振分量品质因子Q1与Q2的相关性需符合式(4)所示条件[19],即满足Q1>Q2。
| $ {\rho _{\max }}\left( {{Q_1},{Q_2}} \right) = \sqrt {\frac{{{Q_2} + 1/2}}{{{Q_1} + 1/2}}} < 1 $ | (4) |
假设信号x1、x2可分别由基函数库S1、S2稀疏表示,则可利用形态分量分析(MCA)建立稀疏分解的目标函数[20]
| $ {J\left( {{W_1},{W_2}} \right) = \left\| {x - {S_1}{W_1} - {S_2}{W_2}} \right\|_2^2 + {\lambda _1}{{\left\| {{W_1}} \right\|}_1} + {\lambda _2}{{\left\| {{W_2}} \right\|}_1}} $ | (5) |
式中,W1和W2分别代表高共振分量x1和低共振分量x2在基函数库S1和S2下的变换系数,λ1及λ2为两组分量的正则化参数。
当目标函数J(W1, W2)达到最小值时,其对应的高品质因子和低品质因子小波变换系数分别记为W1和W2,则信号分离所得高、低共振分量可分别表示为
小波包分析是小波理论在信号处理应用领域的一个重大发展,是一种比小波分解更加精细的信号分解方法[22-23]。小波基函数的合理选取是小波包分解准确的前提,相比于第一代小波,本文选用的基于邻域相关性的冗余第二代小波可有效提取更为丰富的特征信息,频率局部化信息更为精确。
第二代小波与第一代小波的区别在于不依赖傅里叶变换,在时间域中实现小波的构造,其分解过程可分为剖分、预测和更新3部分[24]。小波相邻系数相关性降噪思想可理解为若当前小波系数包含有用信号特征,那么和它相邻的2个小波系数也包含该信号的特征[25]。
冗余第二代小波包信号分解层数的合理选取是信号特征快速准确提取的关键,过多的分解层数将导致信号失真与计算量激增,而过少的分解层数则会降低信号的去噪效果,可参考式(6)选取冗余第二代小波包分解层数。
| $ L \le {\log _2}\frac{{{F_{\rm{s}}}}}{{3{F_{\rm{d}}}}} $ | (6) |
式中,L代表最大分解层数,实际工程运用时一般选取3~6层;Fs为采样频率;Fd为故障特征频率。
使用特定预测算子与更新算子对输入信号进行预测及更新计算,设定原始信号序列为s,令c0=s,则其分解过程如式(7)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {{d_{l + 1}} = {c_l} - {P^l}{c_l}}\\ {{c_{l + 1}} = {c_l} + {U^l}{d_{l + 1}}} \end{array}} \right. $ | (7) |
式中,l代表分解层数;cl和dl分别代表冗余第二代小波分解后所得逼近信号及细节信号,其序列长度与输入信号相同;Pl与Ul分别代表第l层的预测算子及更新算子。
信号第j次重构时,定义Ruj(cl+1, dl+1)为通过反更新运算所得信号,Rpj(cl+1, dl+1)为通过反预测运算所得信号,其计算过程可参考式(8)。
| $ \left\{ {\begin{array}{*{20}{l}} {R_{\rm{u}}^j\left( {{c_{l + 1}},{d_{l + 1}}} \right) = {c_{l + 1}} - {U^l}{d_{l + 1}}}\\ {R_{\rm{p}}^j\left( {{c_{l + 1}},{d_{l + 1}}} \right) = {d_{l + 1}} + {P^l}{c_l}} \end{array}} \right. $ | (8) |
经基于邻域相关性的冗余第二代小波变换去噪算法处理后,所得重构信号如式(9)所示。
| $ {c_j} = \frac{1}{2}\left[ {R_{\rm{u}}^j\left( {{c_{l + 1}},{d_{l + 1}}} \right) + R_{\rm{p}}^j\left( {{c_{l + 1}},{d_{l + 1}}} \right)} \right] $ | (9) |
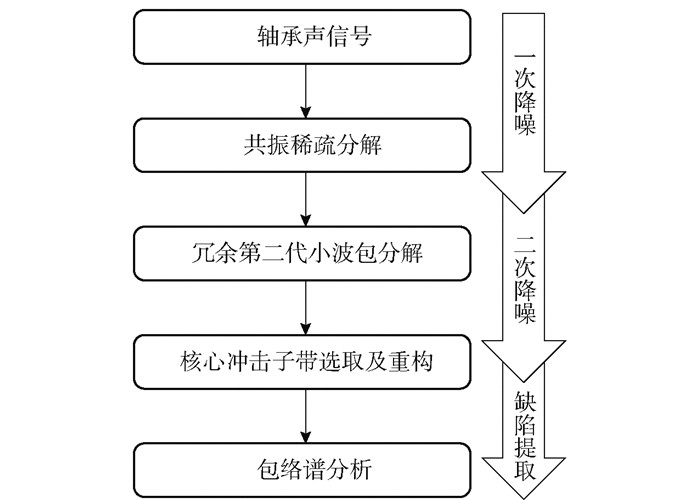
当滚动轴承发生故障时,声音传感器采集所得信号包含转子、轴承等旋转部件产生的周期性冲击信号,以及大量的空气动力性噪声、电磁性噪声、施工干扰噪声及人员交流噪声等环境干扰信号,其中周期性冲击信号在传递过程中衰减较快,受环境干扰较大。周期信号主要承载经传递路径高频调制的冲击信息,是分析提取轴承故障特征的目标信号,属于瞬态冲击成分,信号强度较小。噪声信号主要由各干扰信号线性叠加而成,冲击信息较少,属于振荡成分,信号强度相对较大。周期信号与噪声信号叠加而成的复杂声信号即为声音传感器采集所得信号。共振稀疏分解算法可以依据信号各成分品质因子的不同,将信号中的瞬态冲击成分与持续振荡成分进行有效分离,从而提高信号的冲击特性。冗余第二代小波包降噪算法可进一步消除非平稳信号对目标信号的干扰,提取信号的冲击成分,实现微弱信号的增强。因此本文首先使用共振稀疏分解算法提取信号的瞬态冲击成分,消除环境非周期性噪声信号对目标信号的干扰,然后利用冗余第二代小波包降噪算法进一步减少周期性信号中非平稳成分对轴承冲击信号的影响,实现信号的二次降噪。本文提出的诊断方法流程如图 2所示,具体实现过程如下。
|
图 2 滚动轴承声学诊断方法流程图 Fig.2 Flow chart of acoustic diagnostic methods for rolling bearings |
1) 信号一次降噪。使用共振稀疏分解算法提取原信号的瞬态冲击成分,实现信号的一次降噪。共振稀疏分解算法需基于信号特点完成高低共振分量品质因子Q、冗余因子r及分解层数l的参数设置。为实现持续震荡成分与含有轴承故障信息的瞬态冲击成分的有效分离,应在满足高、低品质因子设定要求的前提下,取得较小的品质因子相关性,减少瞬态冲击信号中持续振荡成分对目标信号的干扰,故设定信号高品质因子Q1=9,低品质因子Q2=1。当冗余因子r≥3时即可实现较好的局部分解性能[26]。为减少算法运算量,提高信号去噪效率,算法设定冗余因子r=3。结合上述参数设定及式(1)~(3)可确定最大分解层数范围。本文所述共振稀疏分解算法各参数设置如表 1所示。
| 下载CSV 表 1 共振稀疏分解参数 Table 1 Resonance sparse decomposition parameters |
2) 信号二次降噪。采用冗余第二代小波包降噪算法对信号低共振分量进行分析,实现信号的二次降噪。小波包降噪算法需结合目标频率及采样频率完成信号分解层数的设置。实际工程应用中,滚动轴承特征频率均为低频信号,基本低于1 kHz,故障轴承声信号受传递路径的高频调制,故障信息主要集中于1~10 kHz频段范围内。结合采样定理与工程应用经验可知,采样频率应大于信号最高频率的2.56倍,即25.6 kHz,代入式(6)计算所得冗余第二代小波包最大分解层数L≤3.09,故设定信号分解层数为3即可满足针对轴承声信号的降噪需求。在对信号进行3层分解所得的8个子带信号中,信号冲击特性均存在一定差异,为进一步提高分析信号中的瞬态冲击成分,从各子带中选取出冲击特征更为明显的子带信号,定义为核心冲击子带。本文选用峭度值作为衡量子带信号冲击特性的特征指标,为减少子带选取数量,尽可能地选取冲击成分更为明显的子带信号。定义若单一子带峭度值大于总峭度平均值的1.5倍时,即判定该子带信号为核心冲击子带信号,各子带峭度值记为ki,当子带属于核心冲击子带信号时,满足式(10)。
| $ {k_j} \ge 1.5 \times \left[ {\left( {\sum\limits_{i = 1}^8 {{k_i}} } \right)/8} \right] $ | (10) |
对选取所得各核心冲击子带信号进行线性叠加并重构,即可得到二次降噪后的轴承声信号,m个核心冲击子带信号的线性叠加过程如式(11)所示。
| $ X = \sum\limits_{j = 1}^m {{x_j}} $ | (11) |
3) 缺陷提取。进行包络谱分析,提取轴承缺陷频率,依据缺陷频率值的大小判断轴承故障类型。
3 方法验证及分析 3.1 故障模拟实验搭建可模拟不同轴承故障的实验台,其左右两侧分别为不可更换正常轴承及可拆卸故障轴承,采用声音传感器在远场条件下对实验产生的声信号进行采集,通过人工播放频率分布广泛的高强度噪声模拟环境噪声干扰,获得比实际工程测量更为复杂的声场环境。实验台基本结构、声音传感器测点布局及外加噪声位置如图 3所示。

|
图 3 故障模拟实验台基本结构及测点布局示意图 Fig.3 Fault simulation test bench basic structure and measurement point layout diagram |
滚动轴承故障模拟实验所用轴承型号为NU205EM,采用线切割加工方式分别在不同轴承内圈加工若干1 mm×0.5 mm的沟槽,在外圈表面加工若干0.5 mm×0.25 mm的沟槽,故障轴承内圈、外圈加工缺陷如图 4所示。

|
图 4 轴承缺陷示意图 Fig.4 Bearing defect diagram |
故障模拟实验过程中,数据采集相关设置及轴承转速基本信息如表 2所示。
| 下载CSV 表 2 轴承故障模拟实验基本参数 Table 2 Basic parameters of the bearing failure simulation experiment |
分别选用外圈轻微、内圈轻微、外圈严重及内圈严重故障轴承进行模拟实验,各组实验轴承故障信息及采集时长如表 3所示。
| 下载CSV 表 3 轴承故障模拟实验信息 Table 3 List of bearing failure simulation experiments |
为验证本文所述轴承声信号降噪方法的准确性,使用所提轴承声学诊断方法对采集所得信号进行分析,并与文献[14]所述方法处理结果进行对比。为直观地显示本文所述降噪方法的有效性,选取去噪后声信号信噪比作为去噪效果评估指标。基于包络谱计算信号信噪比R的过程如式(12)所示[27]。
| $ R = 10\lg \frac{{Y\left( {{K_0}} \right)}}{{\sum\limits_{K = 1}^{N/2} Y (K) - Y\left( {{K_0}} \right)}} $ | (12) |
式中,K0为信号特征频率,Y(K)为信号包络谱中谱线峰值,N为信号长度。
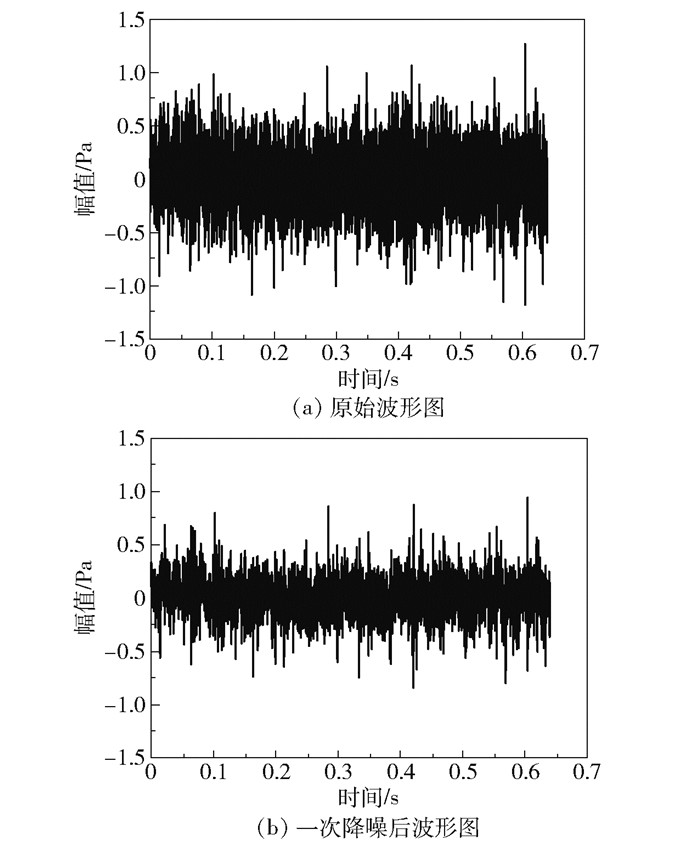
3.2.1 数据处理轴承故障诊断中,外圈故障由于传递路径相对简单,信号有效信息损失少,特征提取难度相比内圈故障较低,因此以内圈轻微划痕故障数据分析结果为例,展示说明本文所述方法在复杂声场环境下对微弱信号提取的有效性。轴承内圈轻微故障声信号原始波形如图 5(a)所示,采用共振稀疏分解算法分析所得一次降噪后信号波形如图 5(b)所示。
|
图 5 内圈轻微故障轴承原始声信号 Fig.5 Original acoustic signal of a slightly faulty inner ring bearing |
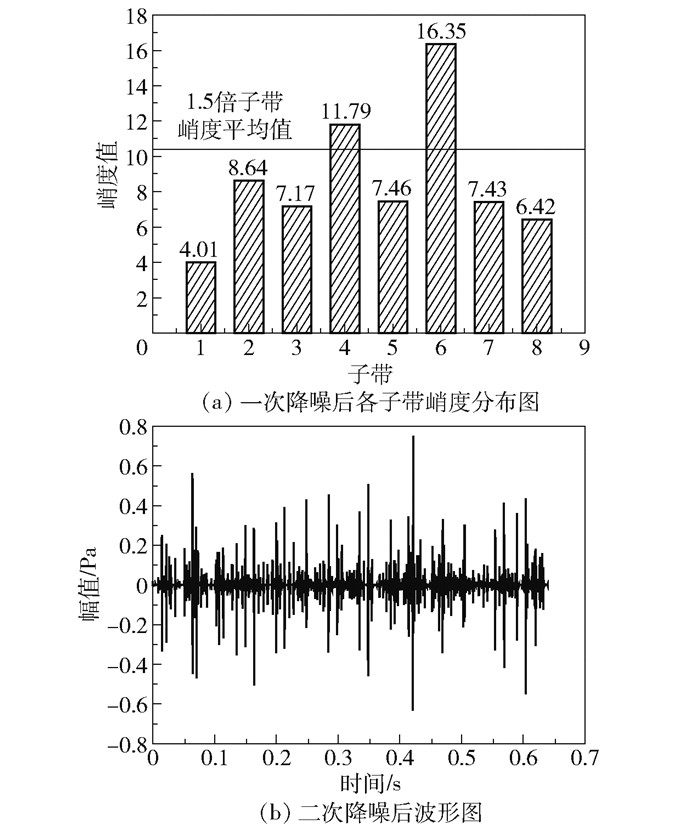
利用冗余第二代小波包算法对一次降噪后信号进行3层分解,各子带信号峭度值计算结果如图 6(a)所示,选取核心冲击子带4及子带6进行线性叠加与信号重构,二次降噪后信号波形如图 6(b)所示。
|
图 6 内圈轻微故障轴承声信号 Fig.6 Slightly faulty inner ring bearing acoustic signal |
对二次降噪后轴承声信号进行包络谱分析,结果如图 7所示。
|
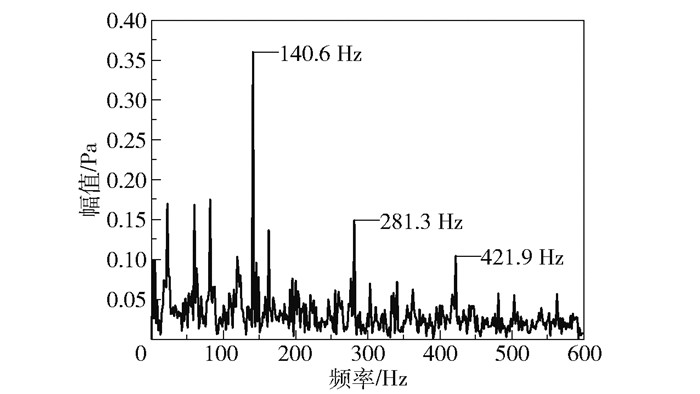
图 7 内圈轻微故障轴承去噪后声信号包络谱图 Fig.7 Envelope spectrum of the acoustic signal of a bearing with a slight inner ring fault after denoising |
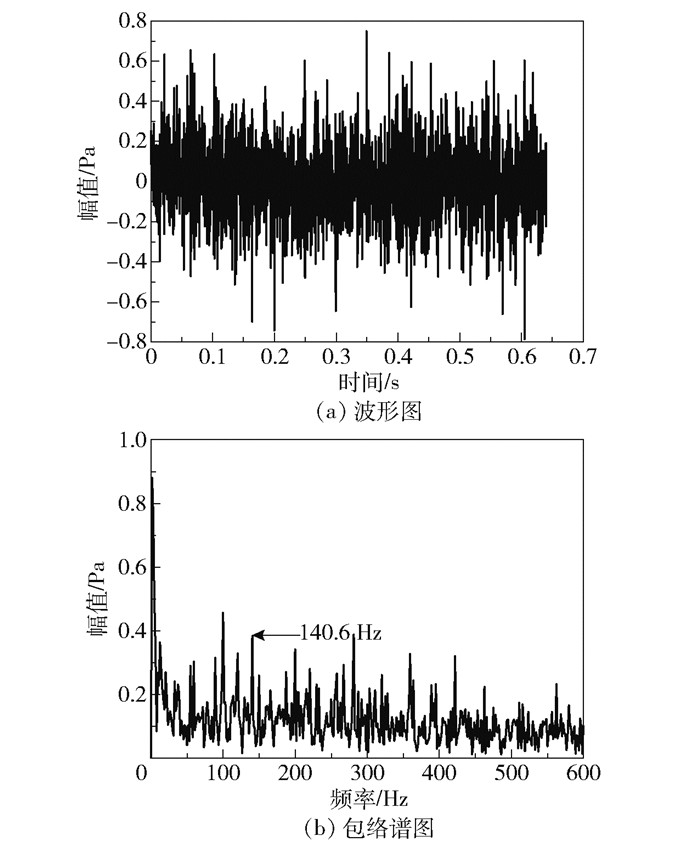
由以上处理结果发现,使用本文所述方法去噪后所得信号较原信号波形冲击成分显著增加,信号去噪效果明显,包络谱中可以读取出明显的特征频率140.6 Hz及其倍频,与轴承内圈理论故障特征频率143.4 Hz基本相同,判断所测轴承故障为内圈故障。
为进一步验证本文所提方法的有效性,采用文献[14]方法对内圈轻微故障轴承原始声信号进行分析,降噪后轴承声信号波形及包络谱图分别如图 8(a)、(b)所示。
对比图 6(b)及图 8(a)可知,文献[14]所述方法处理所得去噪后信号中的波形成分更为复杂,信号去噪效果一般。图 8(b)所示包络谱中同样可以读取出140.6 Hz的内圈故障特征频率,但存在大量幅值相对较高的干扰成分,轴承缺陷特征提取效果相对较差。
为进一步验证所提方法对各类故障轴承声信号降噪的有效性,利用式(12)分别计算原始声信号、本文方法及文献[14]方法处理所得降噪后声信号的信噪比,4组模拟实验分析结果如表 4所示。
| 下载CSV 表 4 降噪后信号及原信号信噪比 Table 4 SNR of the signal after noise reduction and the original signal |
由表 4结果可知,使用本文方法处理所得各组信号的信噪比均高于文献[14]方法分析所得结果,表明本文方法在复杂声场环境下可以有效提取轴承故障信息,提高分析信号质量,信号去噪效果显著。
3.2.2 结果分析对比3.2.1节分析结果可以看出,本文方法相比于文献[14]方法去噪所得波形中信号冲击成分明显增加,在去噪后信号包络谱中可以读取出更为明显的轴承缺陷频率及其倍频等故障信息。对于各种故障类型及不同严重程度的轴承声信号,本文方法均可有效提高分析信号的信噪比,去噪效果明显。文献[14]方法以原信号低共振分量峭度值作为共振稀疏分解算法参数设置依据,特征提取效果易受环境噪声干扰且增加了算法运算量,选用小波包分解后各子带能量值作为子带冲击特性指标来选取重构子带,易受到高强度非平稳信号的干扰,无法准确获取包含轴承故障信息的冲击子带,导致信号去噪效果一般。
本文方法依据采集所得信号中周期性信号与噪声信号冲击特性的不同,设置可实现目标成分与干扰成分有效分离的高、低品质因子及冗余因子等基本参数,在减少运算量的同时确保了周期性信号的准确提取,实现信号的一次降噪。分离所得信号低共振分量中除故障轴承信号外,还含有大量设备其他部件振动引起的非平稳信号,冗余第二代小波包去噪算法可以有效减少高强度非平稳信号对轴承冲击信号的干扰,更好地保留轴承故障信息。以子带峭度值作为小波包降噪后核心冲击子带的选取依据,可精确衡量子带信号的冲击特征,进一步消除电机、联轴器等部件振动对轴承信号的干扰,实现针对轴承声信号的二次降噪。
以上滚动轴承故障诊断的实例与分析结果表明,本文方法在复杂声场环境下去噪效果明显,可有效提高信号的冲击特性,在基于声信号的滚动轴承故障诊断中有良好的应用效果。
4 结论(1) 本文提出的复杂声场环境下信号二次降噪方法解决了声信号轻微冲击信息提取困难的问题,对于其他复杂监测环境下微弱信号的增强具有一定的参考价值。
(2) 本文提出的滚动轴承冲击信号提取方法能够有效降低设备其他振动对目标信号的干扰,对解决轴承振动信号的降噪问题具有一定的借鉴意义。
(3) 本文提出的轴承声学诊断方法可以有效消除噪声干扰,提取轴承微弱故障信息,实现复杂声场环境下基于声信号的滚动轴承故障诊断。
| [1] |
胡超凡, 王衍学. 基于张量分解的滚动轴承复合故障多通道信号降噪方法研究[J]. 机械工程学报, 2019, 55(12): 50-57. HU C F, WANG Y X. Research on multi-channel signal denoising method for multiple faults diagnosis of rolling element bearings based on tensor factorization[J]. Journal of Mechanical Engineering, 2019, 55(12): 50-57. (in Chinese) |
| [2] |
马波, 翟斌, 彭琦, 等. 基于不同退化阶段状态空间模型及粒子滤波的滚动轴承寿命预测[J]. 北京化工大学学报(自然科学版), 2017, 44(3): 83-88. MA B, ZHAI B, PENG Q, et al. Useful life prediction of rolling element bearings based on a particle filtering model and the state space model at different degradation stages[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2017, 44(3): 83-88. (in Chinese) |
| [3] |
王林, 蔡改改, 高冠琪, 等. 基于改进MP的稀疏表示快速算法及其滚动轴承故障特征提取应用[J]. 振动与冲击, 2017, 36(3): 176-182. WANG L, CAI G G, GAO G Q, et al. Fast sparse representation algorithm based on improved MP and its applications in fault feature extraction of rolling bearings[J]. Journal of Vibration and Shock, 2017, 36(3): 176-182. (in Chinese) |
| [4] |
ZHENG J D, CHENG J S, YANG Y. Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing[J]. Signal Processing, 2014, 96: 362-374. DOI:10.1016/j.sigpro.2013.09.013 |
| [5] |
AL-GHAMD A M, MBA D. A comparative experimental study on the use of acoustic emission and vibration analysis for bearing defect identification and estimation of defect size[J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1537-1571. DOI:10.1016/j.ymssp.2004.10.013 |
| [6] |
吴军彪, 陈进, 钟平, 等. 声学故障诊断中的宽带相关噪声信号分离方法[J]. 振动、测试与诊断, 2003, 23(1): 26-29. WU J B, CHEN J, ZHONG P, et al. Separation of wide-band coherent noise signals in acoustic based diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2003, 23(1): 26-29. (in Chinese) |
| [7] |
AMARNATH M, KRISHNA I R P. Empirical mode decomposition of acoustic signals for diagnosis of faults in gears and rolling element bearings[J]. IET Science, Measurement and Technology, 2012, 6(4): 279-287. DOI:10.1049/iet-smt.2011.0082 |
| [8] |
LAW L S, KIM J H, LIEW W Y H, et al. An approach based on wavelet packet decomposition and Hilbert-Huang transform (WPD-HHT) for spindle bearings condition monitoring[J]. Mechanical Systems and Signal Processing, 2012, 33: 197-211. DOI:10.1016/j.ymssp.2012.06.004 |
| [9] |
周俊, 伍星, 迟毅林, 等. 盲解卷积和频域压缩感知在轴承复合故障声学诊断的应用[J]. 机械工程学报, 2016, 52(3): 69-76. ZHOU J, WU X, CHI Y L, et al. Blind deconvolution and frequency domain compressive sensing application in bearing composite acoustic fault diagnosis[J]. Journal of Mechanical Engineering, 2016, 52(3): 69-76. (in Chinese) |
| [10] |
鲁文波, 蒋伟康. 利用声场空间分布特征诊断滚动轴承故障[J]. 机械工程学报, 2012, 48(13): 68-72. LU W B, JIANG W K. Diagnosing rolling bearing faults using spatial distribution features of sound field[J]. Journal of Mechanical Engineering, 2012, 48(13): 68-72. (in Chinese) |
| [11] |
SELESNICK I W. Resonance-based signal decomposition: a new sparsity-enabled signal analysis method[J]. Signal Processing, 2011, 91(12): 2793-2809. DOI:10.1016/j.sigpro.2010.10.018 |
| [12] |
王新华, 齐立夫, 陈迎春, 等. 管道损伤磁梯度共振稀疏分解与BMSR辨识方法[J]. 振动、测试与诊断, 2019, 39(6): 1316-1323, 1367. WANG X H, QI L F, CHEN Y C, et al. Magnetic gradient resonance sparse decomposition and BMSR identification method for pipeline damage[J]. Journal of Vibration, Measurement & Diagnosis, 2019, 39(6): 1316-1323, 1367. (in Chinese) |
| [13] |
孙云嵩, 于德介, 陈向民, 等. 基于信号共振稀疏分解的阶比分析及其在齿轮故障诊断中的应用[J]. 振动与冲击, 2013, 32(16): 93-99. SUN Y S, YU D J, CHEN X M, et al. Order domain analysis based on resonance-based sparse signal decomposition and its application to gear fault diagnosis[J]. Journal of Vibration and Shock, 2013, 32(16): 93-99. (in Chinese) |
| [14] |
陈保家, 汪新波, 严文超, 等. 采用品质因子优化和子带重构的共振稀疏分解滚动轴承故障诊断方法[J]. 西安交通大学学报, 2018, 52(4): 70-76, 89. CHEN B J, WANG X B, YAN W C, et al. A RSSD fault diagnosis method for rolling bearings based on optimization of quality factors and reconstruction of sub-bands[J]. Journal of Xi'an Jiaotong University, 2018, 52(4): 70-76, 89. (in Chinese) |
| [15] |
赵乐, 杨绍普, 刘永强, 等. 基于稀疏分解和频域相关峭度的轴承微弱故障特征提取[J]. 振动与冲击, 2019, 38(23): 196-202, 212. ZHAO L, YANG S P, LIU Y Q, et al. Weak fault feature extraction of bearing based on sparse decomposition and frequency domain correlation kurtosis[J]. Journal of Vibration and Shock, 2019, 38(23): 196-202, 212. (in Chinese) |
| [16] |
陈向民, 于德介, 李蓉. 基于信号共振稀疏分解与重分配小波尺度谱的转子碰摩故障诊断方法[J]. 振动与冲击, 2013, 32(13): 27-33. CHEN X M, YU D J, LI R. Rub-impact diagnosis of rotors with resonance-based sparse signal decomposition and reassigned wavelet scalogram[J]. Journal of Vibration and Shock, 2013, 32(13): 27-33. (in Chinese) |
| [17] |
DING J M, ZHAO W T, MIAO B R, et al. Adaptive sparse representation based on circular-structure dictionary learning and its application in wheelset-bearing fault detection[J]. Mechanical Systems and Signal Processing, 2018, 111: 399-422. DOI:10.1016/j.ymssp.2018.04.012 |
| [18] |
杨伟, 王红军. 基于改进的共振稀疏分解的滚动轴承故障诊断[J]. 机床与液压, 2019, 47(16): 175-179. YANG W, WANG H J. Fault diagnosis of rolling bearing based on improved resonance sparse decomposition[J]. Machine Tool & Hydraulics, 2019, 47(16): 175-179. (in Chinese) |
| [19] |
SELESNICK I W. Resonance-based signal decomposition: a new sparsity-enabled signal analysis method[J]. Signal Processing, 2011, 91(12): 2793-2809. DOI:10.1016/j.sigpro.2010.10.018 |
| [20] |
李星, 于德介, 张顶成. 基于最优品质因子信号共振稀疏分解的滚动轴承故障诊断[J]. 振动工程学报, 2015, 28(6): 998-1005. LI X, YU D J, ZHANG D C. Fault diagnosis of rolling bearings based on the resonance-based sparse signal decomposition with optimal Q-factor[J]. Journal of Vibration Engineering, 2015, 28(6): 998-1005. (in Chinese) |
| [21] |
王霄, 谢平, 郭源耕, 等. 基于多字典-共振稀疏分解的脉冲故障特征提取[J]. 中国机械工程, 2019, 30(20): 2456-2462. WANG X, XIE P, GUO Y G, et al. Impulse fault signature extraction based on multi-dictionary resonance-based sparse signal decomposition[J]. China Mechanical Engineering, 2019, 30(20): 2456-2462. (in Chinese) |
| [22] |
张智, 刘成颖, 刘辛军, 等. 采用小波包能量熵的铣削振动状态分析方法研究[J]. 机械工程学报, 2018, 54(21): 57-62. ZHANG Z, LIU C Y, LIU X J, et al. Analysis of milling vibration state based on the energy entropy of WPD[J]. Journal of Mechanical Engineering, 2018, 54(21): 57-62. (in Chinese) |
| [23] |
罗荣, 田福庆, 冯昌林, 等. 冗余小波包改进及其在齿轮箱故障诊断中应用[J]. 机械工程学报, 2014, 50(15): 82-88. LUO R, TIAN F Q, FENG C L, et al. Improved redundant wavelet packet decomposition and its application in gearbox fault diagnosis[J]. Journal of Mechanical Engineering, 2014, 50(15): 82-88. (in Chinese) |
| [24] |
崔玲丽, 高立新, 殷海晨, 等. 基于第二代小波的复合故障诊断方法研究[J]. 中国机械工程, 2009, 20(4): 442-446. CUI L L, GAO L X, YIN H C, et al. Research on composite fault diagnosis method based on the second generation wavelet[J]. China Mechanical Engineering, 2009, 20(4): 442-446. (in Chinese) |
| [25] |
姜洪开, 何正嘉, 段晨东. 冗余第2代小波构造及机械信号特征提取[J]. 西安交通大学学报, 2004, 38(11): 1140-1142, 1164. JIANG H K, HE Z J, DUAN C D. Construction of redundant second generation wavelet and mechanical signal feature extraction[J]. Journal of Xi'an Jiaotong University, 2004, 38(11): 1140-1142, 1164. (in Chinese) |
| [26] |
黄文涛, 付强, 窦宏印. 基于自适应优化品质因子的共振稀疏分解方法及其在行星齿轮箱复合故障诊断中的应用[J]. 机械工程学报, 2016, 52(15): 44-51. HUANG W T, FU Q, DOU H Y. Resonance-based sparse signal decomposition based on the quality factors optimization and its application of composite fault diagnosis to planetary gearbox[J]. Journal of Mechanical Engineering, 2016, 52(15): 44-51. (in Chinese) |
| [27] |
ZHANG H B, HE Q B, LU S L, et al. Stochastic resonance with a joint Woods-Saxon and Gaussian potential for bearing fault diagnosis[J]. Mathematical Problems in Engineering, 2014(1): 315901. |