非线性Schrödinger方程最开始用于非均匀介质波的研究,后广泛用于非线性光学、等离子物理等领域[1-4]。对于带五次项的此类方程的显示解以及解的性质已有学者进行了深入的研究[5-7]。基于此,本文考虑如下的Schrödinger方程
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{i}}{u_t} + {u_{xx}} - \left( {|u{|^2} + |u{|^4}} \right)u = f(x,t)u,\\ (x,t) \in (a,b) \times (0,1) \end{array} $ | (1) |
其初边值为
| $ u(x,0) = {u_0}(x),x \in [a,b] $ | (2) |
| $ u(0,t) = u(1,t) = 1,t \in [0,T] $ | (3) |
式中u为未知函数,f(x, t)为给定的实函数,u0(x)为给定的复函数。容易证明此方程满足电荷守恒,即满足
| $ Q(t) = \int_a^b | u(x,t){|^2}{\rm{d}}x = Q(0) $ | (4) |
对于此方程Zhang等[8]构造了一个差分格式,收敛阶为O(τ2+h2),初日辉[9]将之改进为紧致格式,收敛阶为O(τ2+h4),魏新新[10]在保持精度不变的前提下引进分裂方法,将原方程分裂为线性子方程和非线性子方程。本文在此基础上进一步改进分裂算法,使其中一个子方程有解析解,以进一步简化计算。
1 数值算法 1.1 符号记文中所用符号的含义为xj=a+jh, j=0, 1, …, J-1;tn=nτ, n=0, 1, …, N-1; Ωh={xj|0≤j≤J-1},Ωτ={tn|0≤n≤N-1},Ωhτ=Ωh×Ωτ。其中h,τ分别为空间和时间步长,J和N为正整数。并记方程在时间节点tn、空间节点xj的差分解为ujn。对Ωhτ上的网格函数Vjn记为lg(h)
| $ {{{\left( {V_j^n} \right)}_x} = \frac{{V_{j + 1}^n - V_j^n}}{h}\quad {{\left( {V_j^n} \right)}_t} = \frac{{V_{j + 1}^n - V_j^n}}{\tau }} $ |
| $ {{{\left( {V_j^n} \right)}_{\bar x}} = \frac{{V_j^n - V_{j - 1}^n}}{h}\quad V_j^{n + \frac{1}{2}} = \frac{{V_j^n + V_j^{n + 1}}}{2}} $ |
| $ {\delta _x^2V_j^n = V_{j + 1}^n - 2V_j^n + V_{j - 1}^n} $ |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_h}V_j^n = \left( {1 + \frac{{{h^2}}}{{12}}\delta _x^2} \right)V_j^n = V_j^n + \frac{{{h^2}}}{{12}}\delta _x^2V_j^n = \left( {V_{j + 1}^n + } \right.\\ \left. {10V_j^n + V_{j - 1}^n} \right)/12 \end{array} $ |
使用时间分裂算法将方程(1)分为两个子方程,使其中一个方程具有解析解,然后对另一个方程进行差分求解,最后将两个子方程结合进行数值求解。
对方程(1),将其表示为
| $ {\rm{i}}\frac{\partial }{{\partial t}}u(x,t) = (A + B)u(x,t) $ | (5) |
式中,算子
| $ {{u^*}(x,t + \tau ) = \exp \left( { - {\rm{i}}B\frac{\tau }{2}} \right)u(x,t)} $ | (6) |
| $ {{u^{**}}(x,t + \tau ) = \exp \left( { - {\rm{i}}A\frac{\tau }{2}} \right){u^*}(x,t + \tau )} $ | (7) |
| $ {u(x,t + \tau ) = \exp \left( { - {\rm{i}}A\frac{\tau }{2}} \right){u^{**}}(x,t + \tau )} $ | (8) |
式中u*(x, t+τ)、u**(x, t+τ)为中间值,该分裂格式误差为O(τ2)。
式(6)、(8)有显式解
| $ u(x,t) = {{\rm{e}}^{ - {\rm{i}}\left( {|u(x,0){|^2} + |u(x,0){|^4}} \right)t}}u(x,0) $ | (9) |
这样只需构造式(7)的差分格式。Strang-type分裂方法在时间上有二阶误差,因此仅从空间方面入手,构造空间四阶格式。
1.3 空间四阶格式对式(6)应用Crank-Nicolson格式,可以得到
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{i}}\frac{{u_j^{n + 1} - u_j^n}}{\tau } + \frac{1}{{2{h^2}}}\delta _x^2\left( {u_j^n + u_j^{n + 1}} \right) = \frac{1}{2}\left( {f_j^{n + \frac{1}{2}}\left( {u_j^n + } \right.} \right.\\ \left. {\left. {u_j^{n + 1}} \right)} \right) \end{array} $ | (10) |
将格式(10)中二阶算子δx2用四阶差分算子
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{i}}{A_h}{\left( {u_j^n} \right)_t} + \frac{{{{\left( {u_j^{n + 1}} \right)}_{x\bar x}} + {{\left( {u_j^n} \right)}_{x\bar x}}}}{2} = \frac{1}{2}{A_h}\left( {f_j^{n + \frac{1}{2}}\left( {u_j^n + } \right.} \right.\\ \left. {\left. {u_j^{n + 1}} \right)} \right) \end{array} $ | (11) |
将式(11)改写为矩阵形式有
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{i}}\mathit{\boldsymbol{A}}\frac{{{\mathit{\boldsymbol{U}}^{n + 1}} - {\mathit{\boldsymbol{U}}^n}}}{\tau } + \mathit{\boldsymbol{B}}\frac{{{\mathit{\boldsymbol{U}}^{n + 1}} + {\mathit{\boldsymbol{U}}^n}}}{{2{h^2}}} = \frac{1}{2}\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{F}}^{n + \frac{1}{2}}}\left( {{\mathit{\boldsymbol{U}}^{n + 1}} + } \right.} \right.\\ \left. {{\mathit{\boldsymbol{U}}^n}} \right) \end{array} $ | (12) |
式中Un表示第n层数值解即(u1n, u2n, …, uJ-1n)T,
矩阵A为
| $ {\left( {\begin{array}{*{20}{c}} {10}&1&0& \cdots &0&0\\ 1&{10}&1& \cdots &0&0\\ 0&1&{10}& \cdots &0&0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0&0& \cdots &{10}&1\\ 0&0&0& \cdots &1&{10} \end{array}} \right)_{(J - 1) \times (J - 1)}} $ |
矩阵B为
| $ {\left( {\begin{array}{*{20}{c}} { - 2}&1&0& \cdots &0&0\\ 1&{ - 2}&1& \cdots &0&0\\ 0&1&{ - 2}& \cdots &0&0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0&0& \cdots &{ - 2}&1\\ 0&0&0& \cdots &1&{ - 2} \end{array}} \right)_{(J - 1) \times (J - 1)}} $ |
将式(12)拆分组合,有
| $ \left( {\frac{{{\rm{i}}\mathit{\boldsymbol{A}}}}{\tau } + \frac{\mathit{\boldsymbol{B}}}{{2{h^2}}} - \frac{{\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{F}}^{\frac{1}{2}}}}}{2}} \right){\mathit{\boldsymbol{U}}^{n + 1}} = \left( {\frac{{{\rm{i}}\mathit{\boldsymbol{A}}}}{\tau } - \frac{\mathit{\boldsymbol{B}}}{{2{h^2}}} + \frac{{\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{F}}^{\frac{1}{2}}}}}{2}} \right){\mathit{\boldsymbol{U}}^n} $ | (13) |
令
| $ \mathit{\boldsymbol{C}} = {\left( {\frac{{{\rm{i}}\mathit{\boldsymbol{A}}}}{\tau } + \frac{\mathit{\boldsymbol{B}}}{{2{h^2}}} - \frac{{\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{F}}^{\frac{1}{2}}}}}{2}} \right)^{ - 1}}\left( {\frac{{{\rm{i}}\mathit{\boldsymbol{A}}}}{\tau } - \frac{\mathit{\boldsymbol{B}}}{{2{h^2}}} + \frac{{\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{F}}^{\frac{1}{2}}}}}{2}} \right) $ | (14) |
这样有
| $ {\mathit{\boldsymbol{U}}^{n + 1}} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{U}}^n} $ | (15) |
式(7)有显式解
| $ u(x,t) = {{\rm{e}}^{ - {\rm{i}}\left( {|u(x,0){|^2} + |u(x,0){|^4}} \right)t}}u(x,0) $ | (16) |
这样有
| $ u(x,t + \Delta t) = {{\rm{e}}^{ - {\rm{i}}\left( {|u(x,t){|^2} + |u(x,t){|^4}} \right)\Delta t}}u(x,t) $ | (17) |
综上所述,时间分裂空间四阶格式可以表示如下。
步骤1
| $ {\mathit{\boldsymbol{U}}^*} = {{\rm{e}}^{ - {\rm{i}}\left( {{{\left| {{\mathit{\boldsymbol{U}}^n}} \right|}^2} + {{\left| {{\mathit{\boldsymbol{U}}^n}} \right|}^4}} \right)\frac{\tau }{2}}}{\mathit{\boldsymbol{U}}^n} $ | (18) |
步骤2
| $ {\mathit{\boldsymbol{U}}^{**}} = C{\mathit{\boldsymbol{U}}^*} $ | (19) |
步骤3
| $ {\mathit{\boldsymbol{U}}^{n + 1}} = {{\rm{e}}^{ - {\rm{i}}\left( {{{\left| {{\mathit{\boldsymbol{U}}^n}} \right|}^2} + {{\left| {{\mathit{\boldsymbol{U}}^n}} \right|}^4}} \right)\frac{\tau }{2}}}{\mathit{\boldsymbol{U}}^{**}} $ | (20) |
式(18)、(20)的Un,Un+1不再表示子方程(7)的数值解,而是原方程(1)的数值解。
1.4 格式电荷守恒定理1 格式(18)~(20)满足电荷守恒
| $ \left\| {{\mathit{\boldsymbol{U}}^{n + 1}}} \right\| = \left\| {{\mathit{\boldsymbol{U}}^n}} \right\| = \cdots = \left\| {{\mathit{\boldsymbol{U}}^0}} \right\| $ | (21) |
由式(12)、(13)易知
| $ \left\| {{\mathit{\boldsymbol{U}}^*}} \right\| = \left\| {{\mathit{\boldsymbol{U}}^n}} \right\| $ |
| $ \left\| {{\mathit{\boldsymbol{U}}^{n + 1}}} \right\| = \left\| {{\mathit{\boldsymbol{U}}^{**}}} \right\| $ |
这样仅需证明
| $ \left\| {{\mathit{\boldsymbol{U}}^*}} \right\| = \left\| {{\mathit{\boldsymbol{U}}^{**}}} \right\| $ |
将式(13)表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{i}}\mathit{\boldsymbol{A}}\frac{{{\mathit{\boldsymbol{U}}^{**}} - {\mathit{\boldsymbol{U}}^*}}}{\mathit{\boldsymbol{\tau }}} + \mathit{\boldsymbol{B}}\frac{{{\mathit{\boldsymbol{U}}^{**}} + {\mathit{\boldsymbol{U}}^*}}}{{2{h^2}}} = \frac{1}{2}\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{F}}^{n + \frac{1}{2}}}\left( {{\mathit{\boldsymbol{U}}^{**}} + } \right.} \right.\\ \left. {\left. {{\mathit{\boldsymbol{U}}^*}} \right)} \right) \end{array} $ |
将上式与向量U**+U*取内积,然后取等式两边,有
| $ \frac{{{{\left\| {{\mathit{\boldsymbol{U}}^{**}}} \right\|}^2} - {{\left\| {{\mathit{\boldsymbol{U}}^*}} \right\|}^2}}}{\mathit{\boldsymbol{\tau }}} = 0 $ |
这样就证明了
| $ \left\| {{\mathit{\boldsymbol{U}}^{n + 1}}} \right\| = \left\| {{\mathit{\boldsymbol{U}}^n}} \right\| $ |
定理1得证。
2 数值实验考虑如下算例
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(x,t) = 4{{(x - 2t)}^2} - \exp \left( { - 2{{(x - 2t)}^2}} \right) - }\\ {\exp \left( { - 4{{(x - 2t)}^2}} \right)} \end{array} $ |
| $ {u_0} = \exp \left( { - {x^2} + {\rm{i}}x} \right) $ |
此时,方程有孤波解
| $ u(x,t) = \exp \left( { - {{(x - 2t)}^2} + {\rm{i}}(x - 3t)} \right) $ |
取Ωh×Ωτ=[-15, 15]×[0, 1],τ=h2,为验证数值格式的收敛性,分别取h=0.5, 0.25, 0.125, 0.062 5,则收敛阶Order可以用下式求得
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Order = \lg \left( {{{\left\| {E(h,\tau )} \right\|}_\infty }/{{\left\| {E\left( {\frac{h}{2},\frac{\tau }{4}} \right)} \right\|}_\infty }} \right)/\\ \lg 2 \end{array} $ |
式中‖E(h, τ)‖∞表示t=1时,数值解在无穷范数下的误差。
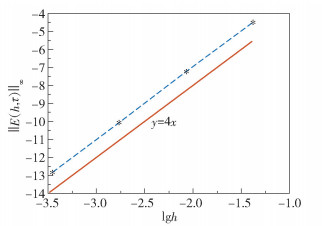
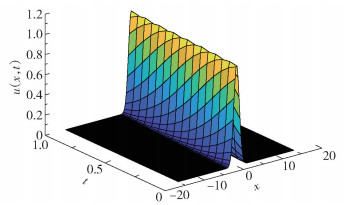
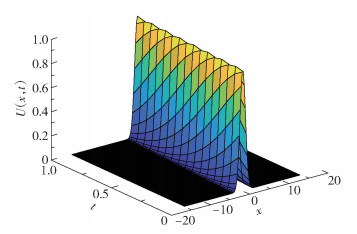
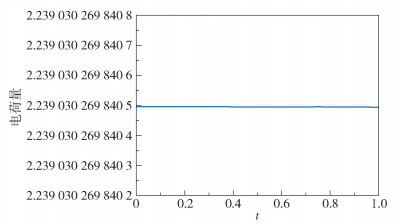
从表 1和图 1可以看出格式以L∞收敛,且收敛阶为O(τ2+h4)。图 2表示τ=0.25时的数值解,图 3表示τ=0.25时的精确解,容易看出两个图像的波形一致。图 4结果表明电荷是守恒的。数值实验与理论相吻合。
| 下载CSV 表 1 不同步长的收敛阶 Table 1 Rates of convergence of different steps |
|
图 1 数值格式的收敛阶 Fig.1 Rate of convergence of the numerical solution |
|
图 2 时间步长为0.25时的数值解 Fig.2 Numerical solution of spatial step 0.25 |
|
图 3 时间步长为0.25时的精确解 Fig.3 Exact solution of spatial step 0.25 |
|
图 4 数值格式的电荷量随时间变化情况 Fig.4 Change in the amount of charge with time |
本文将分裂算法和紧致差分格式相结合对五次非线性Schrödinger方程建立差分格式,格式的收敛阶为O(τ2+h4),并满足离散的电荷守恒定律。数值实验结果验证了本文理论的正确性。
| [1] |
HUANG Z Y, JIN S, MARKOWICH P A, et al. A Bloch decomposition based split-step pseudospectral method for quantum dynamics with periodic potentials[J]. SIAM Journal on Scientific Computing, 2007, 29(2): 515-538. DOI:10.1137/060652026 |
| [2] |
SALMAN H. A time-splitting pseudospectral method for the solution of the Gross-Pitaevskii equations using spherical harmonics with generalised-Laguerre basis functions[J]. Journal of Computational Physics, 2014, 258: 185-207. DOI:10.1016/j.jcp.2013.10.009 |
| [3] |
LIAO F, ZHANG L M, WANG S S. Time-splitting combined with exponential wave integrator Fourier pseudospectral method for Schrödinger-Boussinesq system[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 55: 93-104. DOI:10.1016/j.cnsns.2017.06.033 |
| [4] |
JI B Q, ZHANG L M. Error estimates of a conservative finite difference Fourier pseudospectral method for the Klein-Gordon-Schrödinger equation[J]. Computers and Mathematics with Applications, 2020, 79(7): 1956-1971. DOI:10.1016/j.camwa.2019.06.028 |
| [5] |
DONG S H, GARCÍA-RAVELO J. Exact solutions of the s-wave Schrödinger equation with Manning-Rosen potential[J]. Physica Scripta, 2007, 75(3): 307-309. DOI:10.1088/0031-8949/75/3/013 |
| [6] |
TAGHIZADEH N, MIRZAZADEH M, FARAHROOZ F. Exact solutions of the nonlinear Schrödinger equation by the first integral method[J]. Journal of Mathematical Analysis and Application, 2011, 374(2): 549-553. DOI:10.1016/j.jmaa.2010.08.050 |
| [7] |
EBAID A, KHALED S M. New types of exact solutions for nonlinear Schrödinger equation with cubic nonlinearity[J]. Journal of Computational and Applied Mathematics, 2011, 235(8): 1984-1992. DOI:10.1016/j.cam.2010.09.024 |
| [8] |
ZHANG L M, CHANG Q S. A conservative numerical scheme for a class of nonlinear Schrödinger equation with wave operator[J]. Applied Mathematics and Computation, 2003, 145(2/3): 603-612. |
| [9] |
初日辉. 带五次项的非线性Schrödinger方程紧致差分格式的研究[D]. 南京: 南京航空航天大学, 2014. CHU R H. Compact difference scheme for solving the nonlinear Schrödinger equation involving quanticterm[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.(in Chinese) |
| [10] |
魏新新. 一类非线性Schrödinger方程分裂步紧致差分算法的研究[D]. 南京: 南京航空航天大学, 2019. WEI X X. Researches on split-step compact difference methods for a class of nonlinear Schrödinger equations[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019. (in Chinese) |








