引言

对于磁流体力学的稳定性研究在地球物理学、天文学、工程学等许多领域都有广泛的应用。Rionero^[1]首先提出非线性磁流体力学中的经典能量法，之后该方法被Joseph^[2]、Straughan^[3]加以应用并推广。

讨论一个无限水平均匀的黏性导电不可压缩的流体层，其中与流体相邻的介质不导电，并且夹层处于共面磁场中，文献[4]通过引入基本变量，利用李雅普诺夫直接法，即通过定义广义能量泛函对该系统层流解的线性和非线性稳定性进行了研究。在此基础上，Xu等^[5]利用无源场的螺旋分解，通过构造新的广义能量泛函对该问题的非线性稳定性进行研究，并将所得结果与文献[4]中的结果对比，发现其文中的吸引域半径不依赖于共面磁场。这两篇文献均给出了层流解稳定的充分条件，且所证明的稳定性是有条件的，即初始扰动必须在某吸引域内。本文通过数值计算来比较文献[4]和^[5]中的吸引域半径在不同雷诺数下的大小，继而得出不同广义能量泛函的优劣性。

1 数学模型

考虑一水平方向无限的、均匀的、不可压缩黏性流体夹层R²×(－d, d)，该流体夹层位于一笛卡儿坐标系Oxyz中，z轴垂直于夹层且与重力方向相反，流体夹层置于均匀的共面磁场H=H₀i+H₁j中，并满足边界条件U(x, y, z, －d)=－V₀i，U(x, y, z, d)= V₀i，其中H、U分别为磁场和速度场，V₀, H₀, H₁∈ $\mathbb{R}$。

设前述共面磁场内的流体夹层系统有层流解，那么其无量纲化后的扰动方程组为^[4]

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_t} + \mathit{\boldsymbol{u}}\nabla \mathit{\boldsymbol{u}} + w{\mathit{\boldsymbol{U}}^\prime }(z)\mathit{\boldsymbol{i}} + \mathit{\boldsymbol{U}}(z){\mathit{\boldsymbol{u}}_x} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_m}\left( {{H_0}{\mathit{\boldsymbol{h}}_z} + {H_1}{\mathit{\boldsymbol{h}}_y} + \mathit{\boldsymbol{h}}\nabla \mathit{\boldsymbol{h}}} \right) - \nabla \lambda + \frac{1}{{Re}}\Delta \mathit{\boldsymbol{u}}\\ {\mathit{\boldsymbol{h}}_t} + \mathit{\boldsymbol{u}}\nabla \mathit{\boldsymbol{h}} + \mathit{\boldsymbol{U}}(z){\mathit{\boldsymbol{h}}_x} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {H_0}{\mathit{\boldsymbol{u}}_x} + {H_1}{\mathit{\boldsymbol{u}}_y} + h{\mathit{\boldsymbol{U}}^\prime }(z)\mathit{\boldsymbol{i}} + \mathit{\boldsymbol{h}}\nabla \mathit{\boldsymbol{u}} + \frac{1}{{Rm}}\Delta \mathit{\boldsymbol{h}}\\ \nabla \mathit{\boldsymbol{u}} = 0\\ \nabla \mathit{\boldsymbol{h}} = 0 \end{array} \right. $

(1)

此时求解区域为R²×(－1, 1)×(0, +∞)，这里$\mathit{\boldsymbol{h}} = \left({{h_1}, {h_2}, {h_3}} \right), \mathit{\boldsymbol{u}} = (u, v, w), \lambda = \frac{p}{{{\rho _0}}} + \frac{{{A_m}|\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{h}}{|^2}}}{2}$，p为控制扰动的第三分量，ρ₀∈$\mathbb{R}$，雷诺数$R e=\frac{V_{0} d}{V}$，磁雷诺数$R m=\frac{V_{0} d}{\eta}, A_{m}=\frac{Q^{2}}{R e R m}$，钱德拉塞卡数$Q^{2}=\frac{\mu H^{2} d^{2}}{\rho_{0} \nu \eta}$，其中ν为运动黏度。同时方程组(1)满足以下初始条件和边界条件

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}}(x,y,z,0) = {\mathit{\boldsymbol{u}}_0}(x,y,z)}\\ {\mathit{\boldsymbol{h}}(x,y,z,0) = {\mathit{\boldsymbol{h}}_0}(x,y,z)} \end{array},{R^2} \times ( - 1,1)} \right. $

(2)

$ \mathit{\boldsymbol{h}} = {\bf{0}},{u_z} = 0,{v_z} = 0,w = 0,z = \pm 1,\forall t > 0 $

(3)

通常情况下，研究稳定性时会假设扰动是关于x、y的周期函数, $\mathscr{P}=\left[-\frac{\pi}{\alpha}, \frac{\pi}{\alpha}\right] \times\left[-\frac{\pi}{\beta}, \frac{\pi}{\beta}\right]$表示基本周期，为排除刚性运动的情况，还将加入下述条件：

$ \int_\varOmega u {\rm{d}}\varOmega = 0,\int_\varOmega \nu {\rm{d}}\varOmega = 0,\varOmega = {\mathscr{P} } \times [ - 1,1] $

(4)

2 文献[4]中的稳定性结论

由于线性稳定性分析通常只能给出稳定的必要条件，用线性稳定性理论判别为稳定的系统很有可能在实际中是不稳定的。因此为得到系统稳定的充分条件一般采用李雅普诺夫直接法进行研究，即定义恰当的广义能量泛函来讨论流动的稳定性。文献[4]基于该思路构造了一个广义能量泛函$E(t) = {E_0}(t) + b{E_1}(t)$, 其中${E_0}(t) = \frac{1}{2}\left[{{{\left\| \varphi \right\|}^2} + } \right.$${\beta {{\left\| {\Delta w} \right\|}^2} + {A_m}\left({{{\left\| {{\varphi ^{(m)}}} \right\|}^2} + \beta {{\left\| {\Delta h} \right\|}^2}} \right) + }$${\left. {{\beta _1}{{\left\| {\nabla {\varphi ^{(m)}}} \right\|}^2}} \right], {E_1}(t) = \frac{1}{2}\left[{{{\left\| {\nabla \mathit{\boldsymbol{u}}} \right\|}^2} + {{\left\| {\nabla \mathit{\boldsymbol{h}}} \right\|}^2} + } \right.}$${{{\left\| {\nabla \left({\nabla \times \mathit{\boldsymbol{u}}} \right)} \right\|}^2} + {{\left\| {\nabla {h_{1x}}} \right\|}^2} + {{\left\| {\nabla {h_{2x}}} \right\|}^2} + }$${\left. {{{\left\| {\nabla {h_{1y}}} \right\|}^2} + {{\left\| {\nabla {h_{2y}}} \right\|}^2}} \right], \varphi = \left({\nabla \times \mathit{\boldsymbol{u}}} \right)\mathit{\boldsymbol{k}}, {\varphi ^{(m)}} = }$${\left({\nabla \times \mathit{\boldsymbol{h}}} \right)\mathit{\boldsymbol{k}}}$。

然后对E(t)求导，并结合方程组(1)及其对应的边界条件，用不等式进行估计化简，可得以下结论：假设$R m < \frac{\pi^{2}}{8 M}$，如果$E(0) < \mathscr{A} ^{-2}$，那么层流解是非线性渐进稳定的，且有$E(t) \leqslant$$E(0)\exp \left\{ { - p\left[{1- \mathscr{}{E^{\frac{1}{2}}}(0)} \right]t} \right\}$。其中M=$\mathop {\max }\limits_{[-1, 1]} \left| {{\mathit{\boldsymbol{U}}^\prime }(z)} \right|, b = \frac{{{k_1}}}{{2{\sigma ^2}}}, \; {k_1} = \frac{1}{{{{\rm{ \mathsf{ π} }}^2}}}\min \left({\frac{{16\beta {M^2}{\mathop{ Re}\nolimits} }}{{\beta {{\rm{ \mathsf{ π} }}^4}}}, } \right.$$\left. {\frac{{16\beta {M^2}Rm}}{{\beta {{\rm{ \mathsf{ π} }}^4}}}, \frac{{{{\rm{ \mathsf{ π} }}^2}}}{{8Re}}, \frac{{{{\rm{ \mathsf{ π} }}^2}}}{{4Rm}}, \frac{{{{\rm{ \mathsf{ π} }}^2}}}{2}\left({\frac{1}{{Rm}} - \frac{{8M}}{{{{\rm{ \mathsf{ π} }}^2}}}} \right)} \right), \beta \ge $$\max \left[{\frac{{64{M^2}R{e^2}}}{{{{\rm{ \mathsf{ π} }}^6}}}, \left({\frac{{64{M^2}Rm}}{{{{\rm{ \mathsf{ π} }}^6}}} + \frac{{4{M^2}}}{{{{\rm{ \mathsf{ π} }}^4}{A_m}Re{{\left({{H_0} + {H_1}} \right)}^2}}} \cdot \frac{1}{{\frac{1}{{Rm}} - \frac{{8M}}{{{{\rm{ \mathsf{ π} }}^2}}}}}} \right)} \right], $${\beta _1} = \frac{{2M}}{{Re{{\left({{H_0} + {H_1}} \right)}^2}{{\rm{ \mathsf{ π} }}^2}}}, p = \frac{2}{{{{\rm{ \mathsf{ π} }}^2}}} \cdot \max \left({\frac{1}{{(Re, Rm)\left({\frac{1}{{{k_1}}} + 1} \right)}}} \right)$，同时不等式中$\mathscr{A}$的表达式如下。

$ \begin{array}{*{20}{l}} \ \ \ \ \ \ \ \ {\mathscr{A} = \frac{{4C}}{{\sqrt {{k_1}} b}}\left[ {Re + {A_m}\sqrt {ReRm} + \sqrt {{A_m}ReRm} + Rm \cdot } \right.}\\ {\left. {\sqrt {{A_m}} } \right] + 2C\sqrt {\frac{2}{{{k_1}b}}} \left[ {Re + \sqrt {ReRm} \left( {{A_m} + 1} \right) + Rm} \right] + 8 \cdot }\\ {\left( {C + C_1^2} \right)\left[ {\sqrt {\frac{{{A_m}ReRm}}{{{k_1}b}}} \left( {\frac{1}{{\sqrt {{A_m}} }} + 1} \right) + \frac{{\sqrt {{A_m}} Rm + Re}}{{\sqrt {{k_1}b} }}} \right] + }\\ {2\left( {C + C_1^2} \right)\left( {\frac{{4\sqrt {{A_m}} Rm + Re}}{{\sqrt {b{k_1}} }} + \frac{1}{b}\sqrt {\frac{{2\beta }}{{{k_1}}}} Re + 4 \cdot } \right.}\\ {\left. {\sqrt {\frac{{2ReRm}}{b}} } \right) + \frac{{2{A_m}}}{{\sqrt {{k_1}b} }}\left[ {C\sqrt {\frac{{2ReRm}}{b}} + 4CRm\sqrt {2\beta {k_1}} + } \right.}\\ {\left. {2CRm + \sqrt 2 \left( {C + 2C_1^2} \right)} \right] + 4Rm\left( {\frac{4}{b}C_1^2\sqrt {\frac{{2{\beta _1}}}{{{k_1}}}} + C_1^2{A_m} \cdot } \right.}\\ {\left. {\sqrt {\frac{{2b}}{{{\beta _1}}}} + 3C\sqrt {\frac{{2{A_m}}}{{\beta {k_1}}}} } \right) + 8CRm\sqrt {\frac{2}{b}} \left( {1 + 2{A_m}} \right) + 8C \cdot }\\ {\sqrt {ReRm} \left( {\frac{2}{{\sqrt b }} + \frac{1}{{\sqrt {\beta {k_1}{A_m}} }}} \right)} \end{array} $

(5)

3 文献[5]中的稳定性结论

文献[5]通过对方程组(1)中的u和h进行极向环形分解，令u=▽×(▽φ×k)+▽ψ×k+f= δ·φ+ ε·ψ+f，h=▽×(▽φ^(m)×k)+▽ψ^(m)×k+f^(m)=δ·φ^(m)+ε·ψ^(m)+f^(m)，其中δ·=(∂_xz·, ∂_yz·, －Δ₂)，ε·=(∂_y·, －∂_x·, 0)，由此消去方程组(1)中的▽λ得到一个新的无量纲扰动方程组。

之后应用李雅普诺夫直接法，定义一个新的能量泛函，再次研究该系统层流解的非线性稳定性。在此对构造及估计化简过程不作过多赘述，直接给出文献[5]中的非线性稳定性结论：假设$R m <\frac{\pi^{2}}{2 M}$，如果$\varepsilon(0)<\mathscr{B}^{-2}$，则对于所有磁雷诺数而言，系统中层流解是非线性条件渐进稳定的，且有ε(t)≤ε(0)exp {－Λ₀min{π², α², β²} · $\left.\left(1-\mathscr{B} \varepsilon^{\frac{1}{2}}(0)\right)\right\} t$。其中ε(t)=ε₀(t)+mε₁(t)，${{\varepsilon _0}(t) = \frac{1}{2}\left\{ {\bar \lambda \left[{{{\left\| {{\nabla _2}\Delta \varphi } \right\|}^2} + {A_m}{{\left\| {{\nabla _2}\Delta {\varphi ^{(m)}}} \right\|}^2}} \right] + } \right.}$${\left. {{{\left\| {{\nabla _2}\psi } \right\|}^2} + {A_m}{{\left\| {{\nabla _2}{\psi ^{(m)}}} \right\|}^2} + {{\left\| f \right\|}^2} + {{\left\| {{f^{(m)}}} \right\|}^2}} \right\}, }$$m = \frac{{{\mathit{\Lambda} _0}A_m^2{{\rm{ \mathsf{ π} }}^6}\bar \lambda }}{{2{M^2}{{\left[{{{\rm{ \mathsf{ π} }}^2}{A_m}{\mathop{ Re}\nolimits} \left({1 + {I_{\alpha \beta }}} \right) + Rm\left({1 + {{\rm{ \mathsf{ π} }}^2}} \right)} \right]}^\prime }}} \cdot $${\frac{1}{{\left({{A_m}Re + Rm} \right)\left({{{\rm{ \mathsf{ π} }}^4}\bar \lambda + {{\rm{ \mathsf{ π} }}^2} + 2} \right)}}, {I_{\alpha \beta }} = \max \left\{ {\frac{1}{{{{\rm{ \mathsf{ π} }}^2}}}, \frac{1}{{{\alpha ^2}}}, } \right.}$${\left. {\frac{1}{{{\beta ^2}}}} \right\}, \quad {\mathit{\Lambda} _0} = \min \left\{ {\frac{{R{m^2}}}{{R{m^2} + R{e^2}\left({1 - \frac{{2MRm}}{{{\pi ^2}}}} \right)}}, } \right.}$${\left. {\frac{{R{e^2}{{\left({1 - \frac{{2MRm}}{{{{\rm{ \mathsf{ π} }}^2}}}} \right)}^2}}}{{R{m^2} + R{e^2}\left({1 - \frac{{2MRm}}{{{{\rm{ \mathsf{ π} }}^2}}}} \right)}}, \frac{1}{2}} \right\}, \bar \lambda = \frac{{{M^2}}}{{2{{\rm{ \mathsf{ π} }}^6}}}\left[{R{e^2} + R{m^2} \cdot } \right.}$${\left. {{{\left({1 - \frac{{2MRm}}{{{{\rm{ \mathsf{ π} }}^2}}}} \right)}^{ - 1}}} \right], {\varepsilon _1}(t) = \frac{1}{2}\left\{ {{{\left\| {\nabla \mathit{\boldsymbol{u}}} \right\|}^2} + {A_m} \cdot {{\left\| {\nabla \mathit{\boldsymbol{h}}} \right\|}^2}} \right\}}$，同时I_αβ中α, β≠0，不等式中$\mathscr{B}$的表达式如下。

$ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} \mathscr{B} \end{array} = \frac{{2\sqrt 2 \left[ {{C_{\alpha \beta }}Rm + {L_{\alpha \beta }}Re + \left( {{L_{\alpha \beta }} + {C_{\alpha \beta }}} \right)R{e^{\frac{1}{2}}}R{m^{\frac{1}{2}}}} \right]}}{{{m^{\frac{1}{2}}}}} + }\\ {\frac{{2\sqrt 2 \left[ {\left( {{C_{\alpha \beta }}Rm + {L_{\alpha \beta }}Re} \right){{\bar \lambda }^{\frac{1}{2}}} + \left( {{L_{\alpha \beta }}{{\bar \lambda }^{\frac{1}{2}}} + {C_{\alpha \beta }}I_{\alpha \beta }^{\frac{1}{2}}} \right)R{e^{\frac{1}{2}}}R{m^{\frac{1}{2}}}} \right]}}{{m\varLambda _0^{\frac{1}{2}}}} + }\\ {\frac{{2\sqrt 2 \left[ {{C_{\alpha \beta }}Rm + 2{L_{\alpha \beta }}Re + \left( {{L_{\alpha \beta }} + {C_{\alpha \beta }}} \right)R{e^{\frac{1}{2}}}R{m^{\frac{1}{2}}}} \right]}}{{m{\rm{ \mathit{ π} }}\varLambda _0^{\frac{1}{2}}}} + }\\ {\frac{{2\sqrt 2 \left( {{L_{\alpha \beta }} + {C_{\alpha \beta }}} \right)R{e^{\frac{1}{2}}}R{m^{\frac{1}{2}}}}}{{m{\rm{ \mathit{ π} }}\varLambda _0^{\frac{1}{2}}A_m^{\frac{1}{2}}}}} \end{array} $

(6)

4 稳定性吸引域半径比较

根据共面磁场中无限均匀的不可压缩黏性流体夹层在两种不同广义能量泛函下的非线性稳定性结论，可以得到对应的稳定性吸引域半径，即：R_[1]=$\mathscr{A}$^－2和R_[2]=$\mathscr{B}$^－2，其中R_[1]表示文献[4]中的稳定性吸引域半径，R_[2]表示文献[5]中的稳定性吸引域半径。

接下来比较不同雷诺数下R_[1]和R_[2]的大小。文献[5]在吸引域半径估计时多次利用嵌入不等式，嵌入不等式常数分别为

$ {C_{\alpha \beta }} = \frac{{\sqrt 3 }}{{{2^{\frac{1}{4}}}{{\rm{ \mathit{ π} }}^{\frac{5}{2}}}{{\left[ {{h^3}(\sqrt 2 - 1)} \right]}^{\frac{1}{2}}}}} + \frac{{{2^{\frac{5}{2}}} \cdot 5{{\left( {1 + {{\rm{ \mathit{ π} }}^{ - 2}}} \right)}^{\frac{1}{2}}}{h^{\frac{3}{5}}}}}{3} $

(7)

$ {L_{\alpha \beta }} = \frac{{\sqrt 3 {I_{\alpha \beta }}}}{{{2^{\frac{1}{4}}}{{\left[ {{\rm{ \mathit{ π} }}{h^3}(\sqrt 2 - 1)} \right]}^{\frac{1}{2}}}}} + \frac{{{2^{\frac{5}{2}}} \cdot 5{{\left( {1 + {I_{\alpha \beta }}} \right)}^{\frac{1}{2}}}{h^{\frac{3}{5}}}}}{3} $

(8)

再观察R_[2]中的剩余常数Λ₀、m、λ, 均与M取值有关, 且$M = \mathop {\max }\limits_{_{[-1, 1]}} \left| {{f^\prime }(z)} \right|$。又因f′(z)为无量纲化后所得，所以为便于比较和计算，假设M=2。类似地，之后涉及嵌入不等式中的常数时，都只考虑h=1和α=β=π这种最简单的情况，而计算R_[1]时，涉及到的嵌入不等式常数C和C₁也与式(7)和式(8)取值一致。

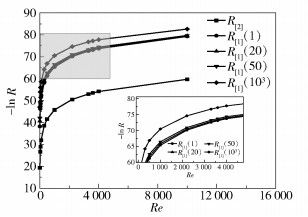
基于上述条件，在之后数值计算求解R_[1]和R_[2]时，只改变雷诺数Re的值，磁雷诺数Rm取定值，即Rm=1，其余常数的赋值情况与前文一致。需注意的是，当计算R_[1]时，H₀+H₁的值也会改变。为便于同R_[2]比较，这里取4组常数进行数值计算，即H₀+H₁=1, 20, 50, 1 000，计算结果如图 1所示。

本文中的吸引域半径小于1，因此靠近横轴的曲线对应较大的吸引域半径。观察图中的曲线可知，当雷诺数增大时，两种不同能量泛函下的吸引域半径均不断变小，说明此时的系统越发不稳定。当共面磁场H的取值为1，20，50和1 000时，无论雷诺数如何取值，R_[2]始终大于R_[1]。

5 结论

对两篇文献中吸引域半径的数值计算结果分析后可得，对本文取定的参数有R_[2]>R_[1]成立。计算表明，文献[4]中的吸引域半径随共面磁场中参数H的增大而减小，这说明对文献[4]中的能量泛函而言，共面磁场可导致层流解的不稳定, 但该计算结果是否能真实地反映实际情况还有待实验验证。与此对照，共面磁场中参数H对于文献[5]中的吸引域半径却无影响, 由此可得文献[5]中的能量泛函在某种程度上优于文献[4]中的能量泛函。

同时，分析文献[4]和^[5]中的能量泛函还发现，两篇文献中的能量泛函均由两部分组成，其中第二部分的泛函是用来控制非线性项的。第二部分泛函的选取直接影响吸引域半径的大小。比较发现，文献[4]中的第二部分泛函远大于文献[5]中的第二部分泛函，这正是导致文献[4]中吸引域半径较小的原因。因此在定义广义能量泛函时第二部分泛函应尽可能的小。