2. 北京化工大学 高端机械装备健康监控及自愈化北京市重点实验室, 北京 100029;
3. 中国航天标准化与产品保证研究院, 北京 100166
2. Beijing Key Laboratory for Health Monitoring Control and Fault Self-Recovery for High-end Machinery, Beijing University of Chemical Technology, Beijing 100029;
3. China Academy of Aerospace Standardization and Product Assurance, Beijing 100166, China
国内炼油与化工生产装置规模大型化发展趋势明显,与其配套的旋转机械设备也向大型化、高速化、自动化和智能化方向发展,而设备故障导致的非计划停机不仅会造成巨大的经济损失,而且可能会带来灾难性的火灾、爆炸等安全事故,因此实现预测性维修对于确保设备安全、可靠运行具有重要作用。故障类型按故障发生、发展的过程分为突发性故障和渐变性故障,一般渐变性故障具有可检测性与可预测性。研究设备性能退化预测技术并开展预测性维修,可使运行维护人员来预防故障或为故障的发生做好充足准备,并最大限度地减少计划外维修带来的损失[1],具有重要的工程应用价值和实践意义。
设备性能退化预测技术是剩余使用寿命预测技术的间接表达,通过预设报警阈值也可以达到寿命预测目的。Pecht等[2]和Lei等[3]将剩余寿命预测方法总体上分为3类:基于机理模型的方法、数据驱动的方法和两者相融合的方法。基于机理模型的方法是在深入分析设备失效机理的基础上建立退化模型,但由于实际运行设备机理模型几乎难以实现导致其应用并不广泛[4]。随着传感技术的发展以及预测和健康管理理念的深入人心,基于数据驱动的退化预测方法引起国内外学者的重视。
系统设备状态数据含有丰富的健康信息,是数据驱动故障诊断和预测技术的基石,其难点在于由历史数据得到的故障预测模型如何延拓,才能保证中长期故障预测的准确性[5]。基于数据驱动的退化预测主要分为统计学习方法与机器学习方法,其中机器学习方法在退化趋势预测中表现出良好的性能。陈强强等[6]采用基于分解-粒化和优化极限学习机的燃油泵性能退化趋势预测,构建退化的置信区间来综合表达设备退化信息;胡友涛等[7]提出了基于小波支持向量回归机和模糊C均值聚类的实时寿命预测方法,利用同类产品的性能退化数据对特定个体的寿命进行实时预测;Wang等[8]采用时间序列分析和反向传播(BP)神经网络相结合的方法对冷却风机进行剩余寿命预测;李志刚等[9]采用径向基神经网络用于继电器寿命预测。然而上述方法都是利用机器学习中的浅层学习机[10](包括支持向量回归、BP神经网络、极限学习机、多层感知机等)预测退化趋势,并未充分发掘数据中的隐含信息。
随着人工智能的发展,深度学习理论在性能退化趋势预测或寿命预测领域逐渐得到应用。吴金栋[11]提出基于动态长短期记忆网络(LSTM)和自回归积分滑动平均模型的发动机剩余寿命预测模型,然而LSTM只是用来提取设备的退化特征并未应用到预测。李京峰等[12]提出基于LSTM与深度置信网络(DBN)的航空发动机剩余寿命预测;张继冬等[13]提出基于全卷积层神经网络的轴承剩余寿命预测;宋亚等[14]提出基于自编码和双向LSTM(Bi-LSTM)的涡扇发动机剩余寿命预测。但以上文献以及目前研究的热点均基于相似模型理论,通过对某一实验室数据或相似工况下的“运转到坏(run to failure)”数据训练后作退化趋势拟合,即知道失效时刻(标签数据)而后反推剩余寿命。然而在实际工厂活动中多变的工况会使实验室训练的模型无法直接应用到实际案例上,相似工况也并不能保证发生的故障相似。同时,目前基于深度学习理念的预测工作往往在模型训练完后再不断地进行预测,并未将预测的数据反馈给数据池重新训练模型以进行下一步预测,固定的模型将会导致累计误差不断增大。
因此,本文提出一种融合趋势滤波、模糊信息粒化、动态长短期记忆网络的旋转机械退化趋势与退化区间预测方法,以振动信号为例,首先提取表达设备性能退化信息的特征指标,然后通过趋势滤波与模糊信息粒化提取主要的退化趋势与模糊退化边界,其次利用动态LSTM模型进行综合的性能退化预测,给出未来时刻设备的主要退化趋势和模糊退化区间。
1 动态LSTM网络性能退化预测模型 1.1 特征提取对于连续采集的旋转机械的振动信号序列而言,有效的特征指标可完整地表达设备的运行可靠性与性能退化状况。何正嘉等[15]对机械设备在运行过程中的可靠性进行评估,提出谱距离指标法、相关系数法、凝聚函数法、状态参量法、信息熵法等一系列归一化的度量指标。对于同一台旋转机械,以运行优良的状态为参考,评估未知状态机械的健康度可采用谱距离指标法。待评估信号与运行优良状态信号的谱距离系数值越大,说明该时刻旋转机械的运行状态越好,谱距离系数越小,说明该时刻旋转机械的运行状态越差[15]。
假设两个信号的功率谱密度函数分别为S1与S2,该两组信号的对称化距离如式(1)所示[16]。
| $ {d^q}\left( {{S_1},{S_2}} \right) = \frac{1}{2}{\left[ {d{{\left( {{S_1},{S_2}} \right)}^q} + d{{\left( {{S_2},{S_1}} \right)}^q}} \right]^{1/q}} $ | (1) |
当q=1,d(S1, S2)=dIS(S1, S2)时,式(2)即成为J散度,计算公式如式(2)。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {J_N}\left( {{S_1},{S_2}} \right) = \frac{1}{2}\left[ {d{{\left( {{S_1},{S_2}} \right)}^q} + d{{\left( {{S_2},{S_1}} \right)}^q}} \right] = \\ \frac{1}{2}\left\| {\frac{{{S_1}}}{{{S_2}}} - \lg \left( {\frac{{{S_1}}}{{{S_2}}}} \right) - 1} \right\| + \frac{1}{2}\left\| {\frac{{{S_2}}}{{{S_1}}} - \lg \left( {\frac{{{S_2}}}{{{S_1}}}} \right) - 1} \right\| = \\ \frac{1}{2}\int {\left( {\frac{{{S_1}}}{{{S_2}}} + \frac{{{S_2}}}{{{S_1}}} - 2} \right)} {\rm{d}}f \end{array} $ | (2) |
则该两信号的谱距离函数H(Jx, y)如式(3)所示。
| $ H\left( {{J_{x,y}}} \right) = \frac{1}{{1 + \alpha {J_{x,y}}}} $ | (3) |
式中,α为灵敏度系数,由设备性能退化趋势决定,α∈(0, 1];Jx, y是良好状态信号x(t)和待评估状态信号y(t)之间的J散度;下标IS表示对称化距离,N表示第N组信号。
1.2 趋势滤波假设一个标准的时间序列yt是由一个基本趋势xt和一个随机变量zt(t=1,…,n)组成。趋势滤波就是从标准的时间序列中估计出基本趋势xt,或者估计出随机变量zt=yt-xt[17]。ℓ1趋势滤波是在Hodrick-Prescot滤波基础上发展来的,使用ℓ1趋势滤波对监测参数趋势数据进行滤波处理,能够很好地得到旋转机械的退化趋势。
ℓ1趋势滤波算法通过最小化加权目标函数实现趋势估计,加权目标函数为
| $ \frac{1}{2}\sum\limits_{t = 1}^n {{{\left( {{y_t} - {x_t}} \right)}^2}} + \lambda \sum\limits_{t = 2}^{n - 1} {\left| {{x_{t - 1}} - 2{x_t} + {x_{t + 1}}} \right|} $ | (4) |
其矩阵形式如式(5)所示。
| $ \frac{1}{2}\left\| {\mathit{\boldsymbol{y-x}}} \right\|_2^2 + \lambda {\left\| {\mathit{\boldsymbol{Dx}}} \right\|_1} $ | (5) |
式中,y=(y1, y2, …,yn)∈Rn,x=(x1, x2, …,xn)∈Rn,‖u‖1=Σi|ui|表示向量u的ℓ1范数,D∈R(n-2)×n是一个二阶差分矩阵。
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 1&{ - 2}&1&{}&{}&{}\\ {}&1&{ - 2}&1&{}&{}\\ {}&{}& \ddots & \ddots & \ddots &{}\\ {}&{}&{}&1&{ - 2}&1 \end{array}} \right] $ | (6) |
λ是一个非负参数用来控制x的平滑性和平衡余项的大小。加权目标函数对x来说是一个严格的凸函数,所以只有一个最小值,用xlt表示,因此xlt就是滤波后的趋势[17]。
文献[18]指出,ℓ1趋势滤波求解问题可以等同于对正则化ℓ1最小二乘求解问题
| $ {\rm{ minimize }}\quad (1/2)\left\| {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda \sum\limits_{i = 3}^n {\left| {{\theta _i}} \right|} $ | (7) |
式中,θ=(θ1,…,θn)∈Rn,A是下三角矩阵
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{}&{}\\ 1&1&{}&{}&{}&{}\\ 1&2&1&{}&{}&{}\\ 1&3&2& \ddots &{}&{}\\ \vdots & \vdots & \vdots & \ddots &1&{}\\ 1&{n - 1}&{n - 2}& \cdots &2&1 \end{array}} \right] \in {{\bf{R}}^{n \times m}} $ | (8) |
通过最小二乘法求得此问题结果θlt,则ℓ1趋势滤波结果xlt=Aθlt。
1.3 模糊信息粒化模糊信息粒化这一概念由Zadeh[19]提出。一个信息整体分解成若干个信息块,每个信息块中的信息元素由于相似、接近或具有某种功能而结合在一起,这样的信息块称为信息粒[20-21]。对于旋转机械退化预测主要分为窗口划分与信息模糊化两个步骤。窗口划分就是将整个时间序列按时间尺度划分为若干个子序列,每个子序列作为一个操作窗口;信息模糊化就是通过一定的模糊规则提取出每个操作窗口的有效退化信息,生成一个个模糊信息粒的过程。信息模糊化的重点是所生成的模糊信息粒能够取代原窗口中的信息,即根据模糊概念G建立的模糊粒子P可以表达模糊窗口X。因此模糊化过程本质上就是确定模糊概念G的隶属函数M的过程。采用三角形模糊粒子求得窗口数据的最大值、最小值和平均值,其隶属函数M可表示为[22]
| $ M(x,a,m,b) = \left\{ {\begin{array}{*{20}{l}} {0,}&{x < a}\\ {\frac{{x - a}}{{m - a}},}&{a \le x \le m}\\ {\frac{{b - x}}{{b - m}},}&{m < x \le b}\\ {0,}&{x > b} \end{array}} \right. $ | (9) |
式中,x是窗口中的变量;a、m、b为参数,分别对应原始数据变化的最小值、平均值和最大值。模糊化后的最小值与最大值即为退化信息的模糊边界。
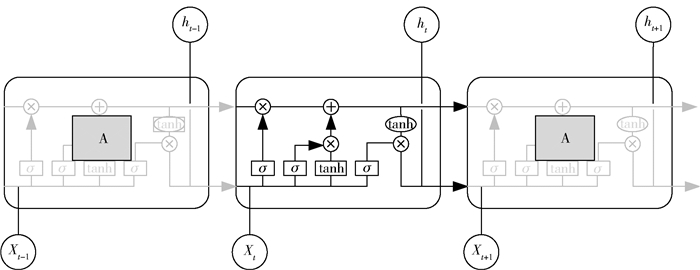
1.4 长短期记忆网络循环神经网络(RNN)是以时间序列为输入,在序列演进方向递归且所有节点(循环单元)按链式递接的递归神经网络。然而一般的RNN存在长期依赖问题,LSTM神经网络的提出解决了该问题,适合处理和预测时间序列中间隔和延迟相对较长的重要事件。如图 1所示,LSTM神经网络每个时间状态的网络拓扑结构相同,在任意t时间下,包含输入层、隐含层和输出层。LSTM的隐含层的输出一分为二,一份传给输出层,一份与下一时刻输入层的输出一起作为隐含层的输入。
|
图 1 LSTM神经网络整体结构 Fig.1 Overall structure of the LSTM neural network |
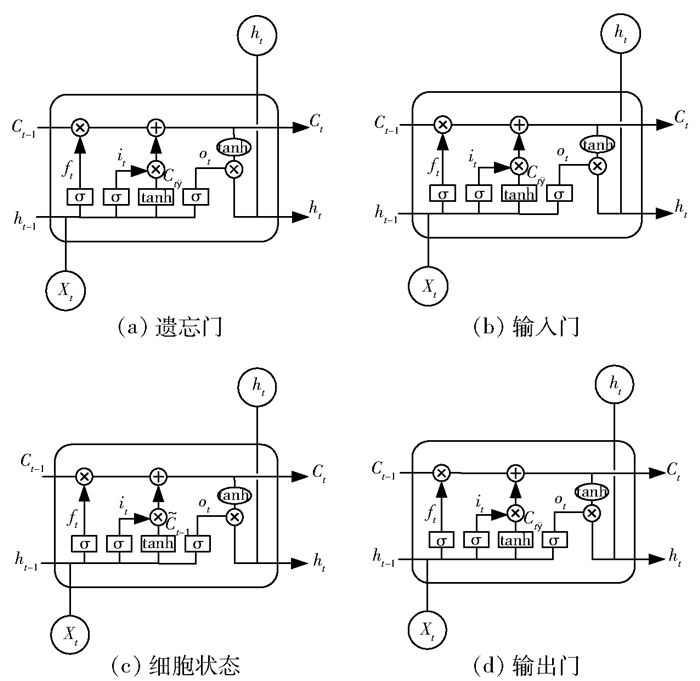
如图 2所示,单个LSTM区块是由遗忘门、输入门、输出门3个门结构和细胞状态构成,贯穿在区块上的水平线为细胞状态,区块内的矩阵是学习的神经网络层,圆圈代表运算操作,箭头表征向量的传输,椭圆为激活函数。
|
图 2 LSTM单元结构 Fig.2 LSTM unit structure |
在遗忘门(图 2(a))中,来自上一层的输出ht-1和本时刻的数据Xt通过sigmoid激活函数进行淘汰与选择,将输入数据进行部分抛弃,具体公式为
| $ {f_t} = \sigma \left\{ {{\mathit{\boldsymbol{W}}_{\rm{f}}}\left[ {{h_{t - 1}},{X_t}} \right] + {b_{\rm{f}}}} \right\} $ | (10) |
式中,Wf、bf为遗忘门的权重矩阵和偏置项;σ为sigmoid函数。
在输入门(图 2(b))中更新单元状态,将部分记忆进行抛弃,部分记忆予以保存,并更新信息。根据式(11)决定更新的信息,根据式(12)计算备选的用来更新的内容。
| $ {{i_t} = \sigma \left\{ {{\mathit{\boldsymbol{W}}_{\rm{i}}}\left[ {{h_{t - 1}},{X_t}} \right] + {b_{\rm{i}}}} \right\}} $ | (11) |
| $ {{{\tilde C}_t} = \tanh \left\{ {{\mathit{\boldsymbol{W}}_{\rm{C}}}\left[ {{h_{t - 1}},{X_t}} \right] + {b_{\rm{C}}}} \right\}} $ | (12) |
式中,Wi、bi为输入门的权重矩阵和偏置项;WC、bC为更新信息时的权重矩阵和偏置项。
在细胞状态(图 2(c))中,来自上一个时刻信息
| $ {C_t} = {f_t} * {C_t} + {i_t} * {\rm{ }}{\tilde C_t} $ | (13) |
在输出门(图 2(d))中,通过式(14)来确定哪些状态作为细胞输出,然后将新的单元状态通过tanh函数计算出输出ht,如式(15)所示。
| $ {{O_t} = \sigma \left\{ {{\mathit{\boldsymbol{W}}_{\rm{o}}}\left[ {{h_{t - 1}},{X_t}} \right] + {b_{\rm{o}}}} \right\}} $ | (14) |
| $ {{h_t} = {O_t} \times \tanh \left( {{C_t}} \right)} $ | (15) |
式中,Wo、bo为输出门的权重矩阵和偏置项。
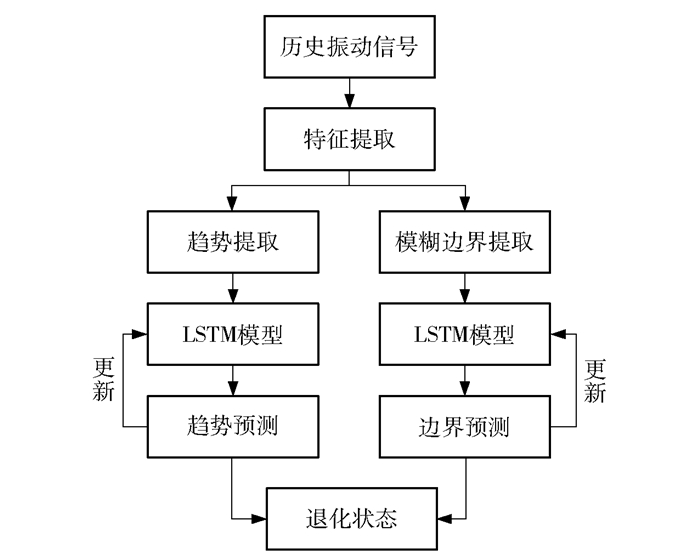
2 退化趋势与模糊退化区间预测方法 2.1 模型构建如图 3所示,首先提取振动信号的特征指标来表达设备的历史退化信息,然后通过趋势滤波与模糊信息粒化提取主要退化趋势与模糊退化边界,之后利用动态LSTM进行模型训练,最终给出综合的性能退化预测。
|
图 3 退化趋势与模糊退化区间预测模型 Fig.3 Prediction model of degradation trends and fuzzy degradation intervals |
在LSTM训练模型中,本文采取的数据处理方式为多步动态预测,多步是指采用前n个时刻数据预测未来l个时刻数据,动态是指将预测l个时刻的数据返回数据池,重新学习模型进行下一次预测,直到达到预测需求。
如式(16)~(18)所示,选择n=5,l=2时,t时刻构造的训练数据为Xt=[xt-4, xt-3, xt-2, xt-1, xt],训练标签为Yt=[xt+1, xt+2]。
| $ {{X_m} = \left[ {{x_{m - n}},{x_{m - n + 1}}, \cdots ,{x_m}} \right]} $ | (16) |
| $ {{X_{{\rm{train }}}} = \left[ {{X_0},{X_1}, \cdots ,{X_m}} \right]} $ | (17) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Y_{{\rm{train }}}} = \left[ {\left[ {{x_1}, \cdots ,{x_l}} \right],\left[ {{x_2}, \cdots ,{x_{l + 1}}} \right], \cdots ,\left[ {{x_{m + 1}},} \right.} \right.\\ \left. {\left. { \cdots ,{x_{l + m + 1}}} \right]} \right] \end{array} $ | (18) |
式中,Xm为m时刻的输入数据,Xtrain为模型的训练数据集,Ytrain为训练数据集的标签。
2.2 参数选择在趋势滤波的过程中,λ是一个非负参数用来控制x的平滑性和平衡余项的大小。由于本文只需要提取主要趋势,且波动状况由模糊边界描述,所以λ可选择尽量大,推荐选择100。
在模糊信息粒化过程中,选择模糊窗口的大小应根据传感器采样间隔与需求决定,一般模糊窗口的大小为10。模糊窗口越大,模糊区间代表的信息也就越多,区间预测波动也会减小,区间更具代表性;模糊窗口越小,模糊区间代表的信息也就越少,区间预测波动会增大,区间更具准确性。
在LSTM模型中,模型的搭建有多种方式,本文选取了简单的单层LSTM模型,由于运行可靠性数据本身已经在[0, 1]区间,所以LSTM不添加归一化层,但为保证批数据的快速运算,添加批归一化层(batch normalization)。优化器采用Adam优化器,参数均为默认。LSTM模型中的超参数用交叉验证方法且结合实际需求(如单次预测与总预测长度)择优。
2.3 性能度量为了公平地比较本文所提方法与其他方法在测试集上的泛化性能,选取均方根误差ERMS(RMSE)来对退化效果进行评价,RMSE值越小,预测效果越好。同时在优化超参数时也采用RMSE作为损失函数。
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{X_{{\rm{predict }},i}} - {X_{{\rm{real }},i}}} \right)}^2}} } $ | (19) |
选取西安交通大学滚动轴承加速寿命实验数据集(XJTU-SY轴承数据集)进行验证,该数据集开展了历时两年的滚动轴承加速寿命实验,共包含3种工况下15个滚动轴承的全寿命周期振动信号,关于轴承信息与传感器采样信息详见文献[23]。
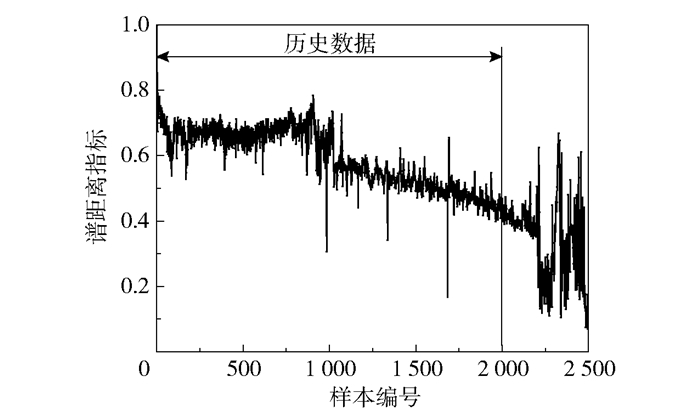
3.2 实验过程及分析 3.2.1 特征指标计算本文以编号Bearing 3_2的数据集为例展示具体实验过程。该数据集样本总数为2 496,采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。以第一组信号为参考,计算其谱距离指标如图 4所示。从图中可以看出,在样本编号1 000点后轴承开始逐步退化,对于大多数复杂机械系统而言,其失效过程大体可分为两个阶段:第一个阶段是从系统安装运行到出现异常的正常工作阶段,在这一阶段监测得到的数据一般比较平稳,没有明显的趋势出现;第二阶段是从出现异常点到系统退化至失效的过程,在这一阶段监测数据将呈现一定的退化趋势[24]。以前1 000~2 000组为已知的历史退化数据对未来一段时间内的数据进行预测。
|
图 4 谱距离指标 Fig.4 Spectral distance index |
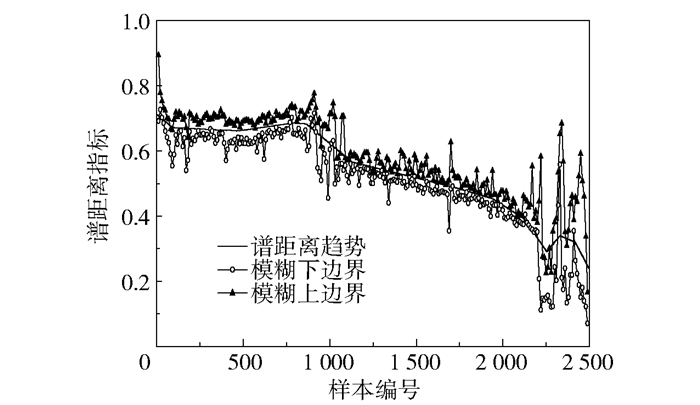
从图 4可以看出,尽管设备的退化信息已较为清楚,但由于采集误差或其他原因,数据间的波动十分明显,因此采用趋势滤波的方法提取设备退化主要趋势,λ依据推荐选择100。设备退化的非趋势项表明了设备的波动状况,通过模糊信息粒化的方式提取设备退化的模糊边界,模糊窗口大小依据推荐选择10,即每个模糊粒子代表长度为10的信息变化。所提取谱距离指标的主要趋势与模糊边界如图 5所示,可以看出设备的退化趋势明显,模糊边界可覆盖主要趋势,因此将历史数据的谱距离趋势与模糊边界作为训练数据构建模型。
|
图 5 谱距离主要趋势与模糊边界 Fig.5 Main trends in spectral distance and fuzzy boundary |
首先在训练数据中分离出验证组作超参数优化。以预测主要趋势为例,其超参数优化过程如表 1所示,其中预测参数32-16的含义为需要前32组数据来预测未来16组数据,MRMSE为在验证组上的平均均方根误差。
| 下载CSV 表 1 超参数优化过程 Table 1 Super-parameter optimization process |
预测模糊边界时超参数优化过程同上,最终采用表 2中的超参数训练LSTM模型。
| 下载CSV 表 2 退化预测与边界预测超参数 Table 2 Super-parameters of degradation prediction and boundary prediction |
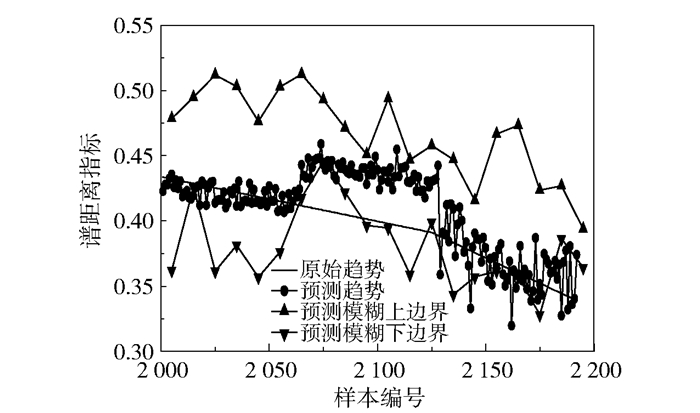
初次趋势预测模型训练后,以历史数据的最后128组数据作为输入预测未来64组数据,而后预测数据返回模型继续训练,共预测未来192组的训练结果。如图 6所示,模糊边界预测模型预测方法同趋势预测,预测未来20个模糊粒子, 每个粒子代表 10组数据,即代表未来200组数据的边界变化情况。
|
图 6 退化趋势与模糊区间预测 Fig.6 Deterioration trend and fuzzy interval prediction chart |
如图 6所示,在预测退化趋势时,设备谱距离指标从0.45下降到0.35左右,虽然第二次模型训练完毕后预测的64组数据距离原始趋势较远,但由于模型的更新,第三次预测就较好地贴合了设备的趋势变化,体现了动态模型的优势。第二次模型的趋势与第一次模型的趋势有一定差别,这是由于每次训练的初始网络都是随机的,所以会导致每次训练的趋势略有不同,但造成的随机误差远小于由于固定模型造成的累计误差。本文模型通过对边界的预测来反映设备退化的置信区间,退化趋势处于设备退化区间内的为可信趋势,处于区间外的为不可信趋势。同时,模糊边界以粒化窗口的形式代表了窗口内所有点的边界变化情况,而趋势预测则反映了每一点的变化情况,从不同的角度反映了退化过程。表 3展示了模糊边界(包括上边界与下边界)与退化趋势的预测精度误差。
| 下载CSV 表 3 退化趋势与模糊区间预测精度 Table 3 Aauracy of degradation trends and fuzzy interval predictions |
为了进一步体现本文所提动态模型方法的优越性,选取其他策略的LSTM模型在编号Bearing 3_2数据集上进行退化趋势的比较分析,其他几种方法分别为传统的LSTM模型和双向长短期记忆网络模型。这两种模型的最优参数均由交叉验证法得出,且列于表 4中。采用全部预测数据的均方根误差作为模型性能指标,采用最后20组预测数据的均方根误差作为模型累计误差的性能比较指标。
| 下载CSV 表 4 其他模型超参数 Table 4 Super-parameters for other models |
对比结果如表 5所示,相比于传统的LSTM模型,Bi-LSTM虽然大幅度提高了预测精度,但仍不能解决累计误差逐渐增大的问题。使用本文提出的动态LSTM预测模型后,后20组数据均方根误差小于整体数据的均方根误差,表明数据累计误差越来越大的问题得到解决。
| 下载CSV 表 5 不同预测方法性能对比 Table 5 Comparison of the performance of different prediction methods |
考虑到实际工厂数据类型与预测需求,本文提出一种融合趋势滤波、模糊信息粒化与动态长短期记忆网络的旋转机械退化趋势与退化区间预测的方法。该方法以运行可靠性理论、趋势滤波理论、模糊信息理论和动态LSTM的模型理论为基础,利用动态LSTM模型预测了设备退化的主要趋势并给出设备退化的模糊区间。实验结果与对比分析表明:本文提出的退化预测方法只需要对设备的退化数据进行分析,即可最终输出未来一定时间段内每一时刻的退化状况以及未来模糊区间时刻内的代表边界,从不同的角度反映了设备的退化信息,且减小了预测累计误差。
| [1] |
MIN J H, KIM D W, PARK C Y. Demonstration of the validity of the early warning in online monitoring system for nuclear power plants[J]. Nuclear Engineering and Design, 2019, 349: 56-62. DOI:10.1016/j.nucengdes.2019.04.028 |
| [2] |
PECHT M G, KANG M. Encyclopedia of structural health monitoring[M]//BOLLER C, CHANG F K, FUJINO Y. Encyclopedia of structural health monitoring. New York: John Wiley & Sons, 2009.
|
| [3] |
LEI Y G, LI N P, GUO L, et al. Machinery health prognostics:a systematic review from data acquisition to RUL prediction[J]. Mechanical Systems and Signal Processing, 2018, 104: 799-834. DOI:10.1016/j.ymssp.2017.11.016 |
| [4] |
蔡忠义, 陈云翔, 郭建胜, 等. 考虑测量误差和随机效应的设备剩余寿命预测[J]. 系统工程与电子技术, 2019, 41(7): 1658-1664. CAI Z Y, CHEN Y X, GUO J S, et al. Remaining lifetime prediction for device with measurement error and random effect[J]. Systems Engineering and Electronics, 2019, 41(7): 1658-1664. (in Chinese) |
| [5] |
陈志强, 陈旭东, de Olivira José Valente, 等. 深度学习在设备故障预测与健康管理中的应用[J]. 仪器仪表学报, 2019, 40(9): 206-226. CHEN Z Q, CHEN X D, DE OLIVIRA J V, et al. Application of deep learning in equipment prognostics and health management[J]. Chinese Journal of Scientific Instrument, 2019, 40(9): 206-226. (in Chinese) |
| [6] |
陈强强, 戴邵武, 戴洪德, 等. 基于分解-粒化和优化极限学习机的燃油泵性能退化趋势预测[J]. 推进技术, 2020, 41(8): 1871-1879. CHEN Q Q, DAI S W, DAI H D, et al. Forecasting of fuel pump performance trend based on decomposition-granulation and optimized extreme learning machine[J]. Journal of Propulsion Technology, 2020, 41(8): 1871-1879. (in Chinese) |
| [7] |
胡友涛, 胡昌华, 孔祥玉, 等. 基于WSVR和FCM聚类的实时寿命预测方法[J]. 自动化学报, 2012, 38(3): 331-340. HU Y T, HU C H, KONG X Y, et al. Real-time lifetime prediction method based on wavelet support vector regression and fuzzy C-means clustering[J]. Acta Automatica Sinica, 2012, 38(3): 331-340. (in Chinese) |
| [8] |
WANG L X, WU Z H, FU Y D, et al. Remaining life predictions of fan based on time series analysis and BP neural networks[C]//IEEE Information Technology, Networking, Electronic & Automation Control Conference. Chongqing: IEEE, 2016: 607-611.
|
| [9] |
李志刚, 刘伯颖, 李玲玲, 等. 基于小波包变换及RBF神经网络的继电器寿命预测[J]. 电工技术学报, 2015, 30(14): 240-247. LI Z G, LIU B Y, LI L L, et al. Life prediction of relay based on wavelet packet transform and RBF neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 240-247. (in Chinese) |
| [10] |
裴洪, 胡昌华, 司小胜, 等. 基于机器学习的设备剩余寿命预测方法综述[J]. 机械工程学报, 2019, 55(8): 1-13. PEI H, HU C H, SI X S, et al. Review of machine learning based remaining useful life prediction methods for equipment[J]. Journal of Mechanical Engineering, 2019, 55(8): 1-13. (in Chinese) |
| [11] |
吴金栋.航空发动机气路故障诊断与预测的机器学习方法研究[D].南京: 南京航空航天大学, 2018. WU J D. Aero engine gas path fault diagnosis and prognosis based on machine learning method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese) |
| [12] |
李京峰, 陈云翔, 项华春, 等. 基于LSTM-DBN的航空发动机剩余寿命预测[J]. 系统工程与电子技术, 2020, 42(7): 1637-1644. LI J F, CHEN Y X, XIANG H C, et al. Remaining useful life prediction for aircraft engine based on LSTM-DBN[J]. Systems Engineering and Electronics, 2020, 42(7): 1637-1644. (in Chinese) |
| [13] |
张继冬, 邹益胜, 邓佳林, 等. 基于全卷积层神经网络的轴承剩余寿命预测[J]. 中国机械工程, 2019, 30(18): 2231-2235. ZHANG J D, ZOU Y S, DENG J L, et al. Bearing remaining life prediction based on full convolutional layer neural network[J]. China Mechanical Engineering, 2019, 30(18): 2231-2235. (in Chinese) |
| [14] |
宋亚, 夏唐斌, 郑宇, 等. 基于Autoencoder-BLSTM的涡扇发动机剩余寿命预测[J]. 计算机集成制造系统, 2019, 25(7): 1611-1619. SONG Y, XIA T B, ZHENG Y, et al. Remaining useful life prediction of turbofan engine based on Autoencoder-BLSTM[J]. Computer Integrated Manufacturing Systems, 2019, 25(7): 1611-1619. (in Chinese) |
| [15] |
何正嘉, 曹宏瑞, 訾艳阳, 等. 机械设备运行可靠性评估的发展与思考[J]. 机械工程学报, 2014, 50(2): 171-186. HE Z J, CAO H R, ZI Y Y, et al. Developments and thoughts of operational reliability assessment of mechanical equipment[J]. Journal of Mechanical Engineering, 2014, 50(2): 171-186. (in Chinese) |
| [16] |
李中.离心压缩机实时健康评估与维修决策研究[D].北京: 北京化工大学, 2019. LI Z. Research on real-time health assessment and maintenance decision of centrifugal compressor[D]. Beijing: Beijing University of Chemical Technology, 2019. (in Chinese) |
| [17] |
张明, 冯坤, 江志农. 基于动态自学习阈值和趋势滤波的机械故障智能预警方法[J]. 振动与冲击, 2014, 33(24): 8-14. ZHANG M, FENG K, JIANG Z N. A mechanical fault early warning methodology based on dynamic self-learning threshold and trend filtering techniques[J]. Journal of Vibration and Shock, 2014, 33(24): 8-14. (in Chinese) |
| [18] |
KIM S J, KOH K, BOYD S, et al. l1 trend filtering[J]. SIAM Review, 2009, 51(2): 339-360. DOI:10.1137/070690274 |
| [19] |
ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X |
| [20] |
LU W, PEDRYCZ W, LIU X D, et al. The modeling of time series based on fuzzy information granules[J]. Expert Systems with Applications, 2014, 41(8): 3799-3808. DOI:10.1016/j.eswa.2013.12.005 |
| [21] |
殷豪, 黄圣权, 刘哲, 等. 基于模糊信息粒化和长短期记忆网络的短期风速预测[J]. 电测与仪表, 2019, 56(11): 101-107. YIN H, HUANG S Q, LIU Z, et al. Short-term wind speed prediction based on fuzzy information granulation and LSTM[J]. Electrical Measurement & Instrumentation, 2019, 56(11): 101-107. (in Chinese) |
| [22] |
甄宗政.基于模糊信息粒化和SVM优化模型的上证指数实证分析[D].兰州: 兰州大学, 2017. ZHEN Z Z. An empirical analysis of Shanghai composite index based on fuzzy information granulation and SVM optimization model[D]. Lanzhou: Lanzhou University, 2017. (in Chinese) |
| [23] |
WANG B, LEI Y G, LI N P, et al. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[J]. IEEE Transactions on Reliability, 2020, 69(1): 401-412. DOI:10.1109/TR.2018.2882682 |
| [24] |
周东华, 魏慕恒, 司小胜. 工业过程异常检测、寿命预测与维修决策的研究进展[J]. 自动化学报, 2013, 39(6): 711-722. ZHOU D H, WEI M H, SI X S. A survey on anomaly detection, life prediction and maintenance decision for industrial processes[J]. Acta Automatica Sinica, 2013, 39(6): 711-722. (in Chinese) |








