自动平衡系统能够在运行过程中实时改变转子的质量分布,从根源上减小或消除转子不平衡振动。目前变质量分布式自动平衡技术在欧美等国家已实现工业应用,如涡桨螺旋桨、高精度磨床等[1-2]。我国的一些高校和科研机构也围绕自动平衡技术进行了多年的研究,并取得一定的研究成果,但多侧重于自动平衡的结构优化以及稳态、非稳态工况下的自动平衡效果分析[3-6],缺乏针对自动平衡控制输入端算法的深入研究。
目前围绕自动平衡的应用[7]及研究[8-10]多基于转子结构均匀且支承刚度各向同性的假设,针对单平面、单一振动测点采用传统的影响系数法进行自动平衡控制。当转子呈各向异性、支承刚度呈非线性时,必然造成自动平衡控制输入信号误差,导致平衡控制效果差甚至平衡失败。针对单一振动传感器所带来的动平衡问题,屈梁生等[11-12]提出了全息谱动平衡技术,综合两个测量方向信号构建工频三维全息谱来进行动平衡,但该方法需添加试重,并需在基频椭圆基础上绘制转子的试重椭圆以及移相椭圆来寻找转子的不平衡位置,计算较复杂,因此适合离线操作,不利于自动平衡系统控制。文献[13-15]提出的全矢动平衡方法,采用轴心轨迹的椭圆长轴(主振矢)作为动平衡影响系数法的振动控制输入矢量,该方法综合考虑了两个方向的振动信号,能够降低单一振动传感器带来的动平衡误判率。
虽然轴心轨迹能表达转子整个平面的振动状况,但时域的轴心轨迹稳定性差,且包含其他频率成分,无法直接用于自动平衡控制。目前针对轴心轨迹的研究大多集中在转子系统的振动故障辨识方面[16],尚无用于自动平衡方面的报道。因此本文以变质量分布式自动平衡为执行装置,借鉴全矢动平衡主振矢概念,充分考虑自动平衡的实时在线特性,提出一种基于轴心轨迹重构的自动平衡控制输入算法,确保在任何条件下均能最大程度地发挥自动平衡的控制效能,达到最高控制精度。
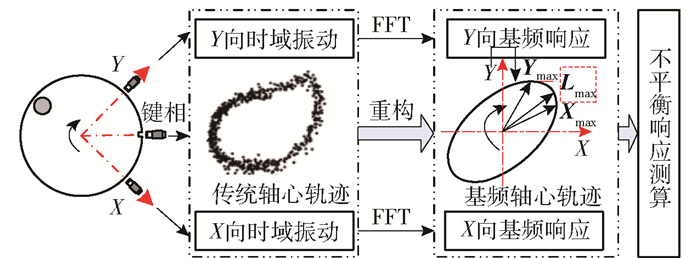
1 轴心轨迹重构原理和方法 1.1 轴心轨迹重构原理在转子测振平面的水平(X轴)和垂直(Y轴)方向分别安装振动位移传感器,获得该截面的轴心轨迹。理想状态下,转子的轴心轨迹为正圆,但是由于转子并非各向同性,所以得到的轴心轨迹一般为椭圆。在实际应用中,故障类型复杂多样,轴心轨迹可能有8字形、香蕉形等多种形状,需要先进行不平衡振动辨识。分别对X轴和Y轴进行快速频谱分析,从传统的轴心轨迹图形中分离出基频特征,再将轴心轨迹重构为椭圆状轨迹,得到椭圆长轴表征的矢量并进行自动平衡控制。轴心轨迹重构工作原理见图 1。
|
图 1 轴心轨迹重构法工作原理 Fig.1 Principle of the axis trajectory reconstruction method |
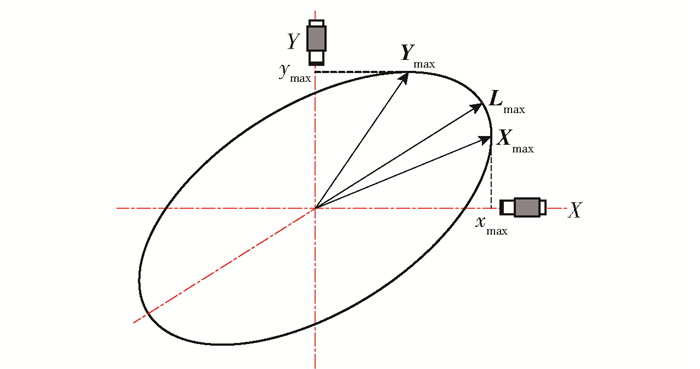
采用X向和Y向传感器进行数据采集,经过快速傅里叶变换(FFT)重构轴心轨迹如图 2所示,X向和Y向的最大振动响应Xmax和Ymax均小于椭圆的长轴矢量Lmax,表明单个传感器无法表征出转子系统的最大振动情况。因此,从重构椭圆中可以看出,Lmax能最大程度地表征系统振动。为考察Lmax是否为自动平衡的最优控制输入信号,需进行理论研究和试验验证。
|
图 2 单/双向传感器采集示意图 Fig.2 Schematic diagram of single/two-way sensor acquisition |
目前在利用转子椭圆轨迹提取长轴和初始相位作为振动响应输入的动平衡技术中,发展较为成熟的是全矢谱技术。该方法将水平方向及垂直方向的整周期信号直接进行数据融合形成复信号,再对复信号进行傅里叶变换得到椭圆长轴及初始相位。但是全矢谱技术仅适用于质量不平衡引起的同频振动,对于存在较高倍频分量及噪声的环境难以有效提取其特征。因此,本文提出基于轴心轨迹重构的自动平衡控制优化算法,其基本思想是:转子的轴心轨迹表达了转子系统各谐波频率的综合作用,而自动平衡系统仅针对转子系统中由于质量不平衡引起的一倍频振动响应,因此基于双传感器的整周期振动信号,重构仅由质量不平衡引起的同频椭圆,进一步提取同频椭圆的长轴及初始相位。
假设水平方向和垂直方向的振动响应分别如式(1)和式(2)所示。
| $ x\left( t \right) = X{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\varphi _0}) + \sum\limits_{i = 1}^N {{X_i}{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_i}t + {\varphi _i})} $ | (1) |
| $ y\left( t \right) = Y{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\phi _0}) + \sum\limits_{i = 1}^N {{Y_i}{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_i}t + {\phi _i})} $ | (2) |
式中,X、Y为同频振动幅值,f0为同频振动频率,φ0、ϕ0为同频振动相位,Xi、Yi为被测信号中倍频分量的幅值,fi为被测信号中倍频分量的频率,φi、ϕi为被测信号中倍频分量的相位。
对原始信号进行快速傅里叶变换获取被测信号的同频振动幅值和相位,再利用同频振动幅值和相位获取水平及垂直方向的同频振动响应分别如式(3)和式(4)所示。
| $x\left( t \right) = X{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\varphi _0}) $ | (3) |
| $ y\left( t \right) = Y{\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\phi _0}) $ | (4) |
将方程(3)、(4)联立可获得转子系统因质量不平衡引起的同频椭圆方程,如式(5)所示。
| $ \begin{array}{l} \;\;\;\frac{{{x^2}}}{{{Y^2}}} - \frac{{2{\rm{cos}}({\phi _0} - {\varphi _0})}}{{XY}}xy + {\rm{sin}}{^2}({\phi _0} - {\varphi _0}){y^2} = \\ {\rm{si}}{{\rm{n}}^2}({\phi _0} - {\varphi _0}) \end{array} $ | (5) |
根据式(5)重构转子运动的同频椭圆,再根据椭圆轨迹计算其长轴L为
| $ \begin{array}{l} \;\;\;\;\;L = {\rm{max\{ }}\sqrt {{x^2} + {y^2}} , \frac{{{x^2}}}{{{Y^2}}} - \frac{{2{\rm{cos}}({\phi _0} - {\varphi _0})}}{{XY}}xy + \\ {\rm{sin}}{^2}({\phi _0} - {\varphi _0}){y^2} = {\rm{sin}}{^2}({\phi _0} - {\varphi _0})\} \end{array} $ | (6) |
将长轴所对应的x、y的坐标记为xmax、ymax,则转子沿同频椭圆运动的初始相位为
| $\alpha = {\rm{arctan}}\frac{{X{\rm{cos}}\;{\varphi _0}}}{{Y{\rm{cos}}\;{\phi _0}}} - {\rm{arctan}}\frac{{{y_{{\rm{max}}}}}}{{{x_{{\rm{max}}}}}} $ | (7) |
最后将式(7)计算得到的Lmax=L∠α作为自动平衡系统的控制输入信号。
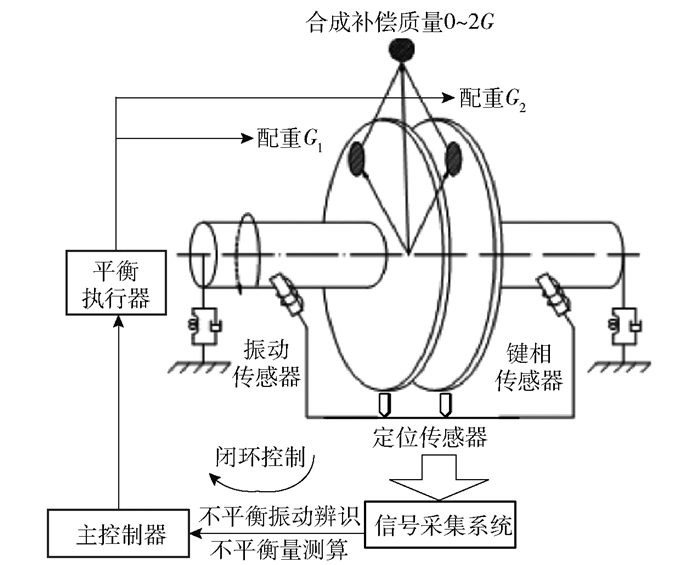
2 轴心轨迹重构法在自动平衡中的应用 2.1 自动平衡控制的基本原理自动平衡控制系统是通过在线移动两个配重(每个配重质量为G)的位置以改变两个配重的夹角来组合出0~2G的补偿质量,实现不平衡振动的实时抑制。自动平衡系统工作原理见图 3。
|
图 3 自动平衡系统工作原理 Fig.3 Principle of the automatic balancing system |
自动平衡系统通过振动和键相传感器获得振动矢量,利用影响系数法进行不平衡振动辨识以及振动响应-不平衡量实时测算,得到补偿质量和相位,将其分解至两配重块后获得两配重块的新目标位置,再向平衡执行器输出配重块驱动命令,完成一次自动平衡任务。
在自动平衡控制系统中,同频振动信号幅值和相位的实时精确提取是决定自动平衡效果的关键。因此,本文采用双传感器采集数据,基于轴心轨迹重构法实现实时精确提取同频信号幅值及相位,并利用影响系数确定配重块的目标位置,然后由无错调控制算法及电磁式双配重自动平衡执行装置,最终实现平衡。
2.2 基于LabVIEW的仿真测试根据轴心轨迹重构法的基本原理,利用LabVIEW虚拟仪器平台编写轴心轨迹重构与提取不平衡振动幅值和相位的仿真程序。在实际的工程应用中,数据采集卡采集到的振动信号非常复杂,因此,用于仿真的虚拟信号要与实际采集到的振动信号尽可能一致。设仿真信号的表达式为
| $\begin{array}{l} \;\;\;\;\;\;x\left( t \right) = {A_0}{\rm{cos}}({\omega _0}t + {\varphi _0}) + \sum\limits_{i = 1}^2 {{A_i}{\rm{cos}}(i{\omega _0}t + {\varphi _i}) + } \\ {x_0}\left( t \right) \end{array} $ | (8) |
| $ \begin{array}{l} \;\;\;\;\;\;\;y\left( t \right) = {B_0}{\rm{cos}}({\omega _0}t + {\phi _0}) + \sum\limits_{i = 1}^2 {{B_i}{\rm{cos}}(i{\omega _0}t + {\phi _i}) + } \\ {y_0}\left( t \right) \end{array} $ | (9) |
式中,A0、B0为一倍频信号的幅值,Ai、Bi为被测信号中倍频分量的幅值,x0(t)、y0(t)为均匀白噪声信号。在模拟X向和Y向单向采集方式时,引入与X向同相位的脉冲信号作为键相信号。仿真程序相关参数设定值如表 1所示,f为模拟工频,采样点数N=2 048,采样频率fS=2 048 Hz。
| 下载CSV 表 1 仿真程序相关参数设定 Table 1 Simulation program parameter settings |
轴心轨迹重构法可以应用于具有复杂倍频信号及噪声的环境。为了模拟转子系统在实际运行中的各种复杂工况,本文模拟3种经典轴心轨迹类型,在仿真信号中分别加入各倍频信号及其组合信号[17]。3类模拟信号的仿真结果如表 2所示。
| 下载CSV 表 2 3类经典轴心轨迹模拟仿真结果 Table 2 Simulation results of three kinds of classical axis trajectories |
由表 2可以看出,轴心轨迹重构法在各种具有倍频分量及噪声的复杂工况中均能精准且稳定地获取模拟信号中的同频椭圆及主振矢。
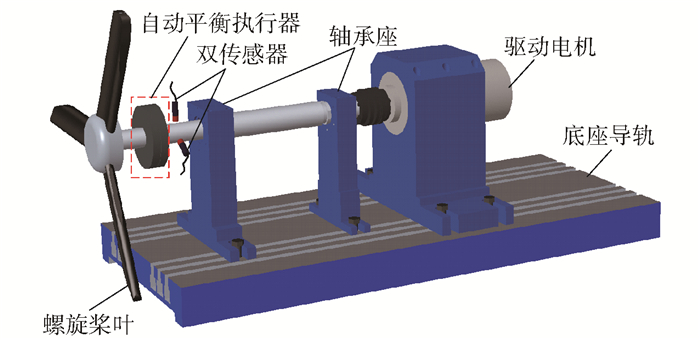
3 试验验证 3.1 自动平衡试验台为了验证轴心轨迹重构法的可行性和实用性,搭建悬臂转子单平面自动平衡试验台,双配重电磁驱动式平衡头安装在悬臂轴上,其测量原理及试验台结构如图 4、5所示。试验过程中,转子轴心轨迹为椭圆且轴心轨迹中心偏离转子的几何中心,说明该转子呈各向异性,支撑刚度非线性。在远离轴承靠近平衡头10 cm处分别安装水平、垂直两个非接触式电涡流传感器,利用LabVIEW软件编程来实现信号采集及实时轴心轨迹重构,分析计算获取主振矢及其相位;利用影响系数法得到补偿质量目标位置,然后由无错调控制移动策略实现转子的在线自动平衡。
|
图 4 悬臂结构自动平衡试验台机理图 Fig.4 Mechanistic illustration of the cantilever structure automatic balancing test bed |

|
图 5 悬臂结构自动平衡试验台 Fig.5 Views of the cantilever structure automatic balancing test bed |
试验转速采用稳定转速1 200 r/min(参考某型号螺旋桨真实转速),分别利用单一水平电涡流传感器、单一垂直电涡流传感器以及轴心轨迹重构法的数据作为自动平衡控制输入,进行自动平衡试验。为了实现数据对比,控制3次试验中补偿质量的初始位置和试重参数均不变,改变双配重初始位置为31.5°、40.5°,试重位置为301.5°、310.5°。
3.2 结果与讨论首先测试初始状态下转子的轴心轨迹,结果见图 6(a),经过轴心轨迹重构后得到图 6(b)。

|
图 6 转子轴心轨迹 Fig.6 Rotor axis trajectory diagram |
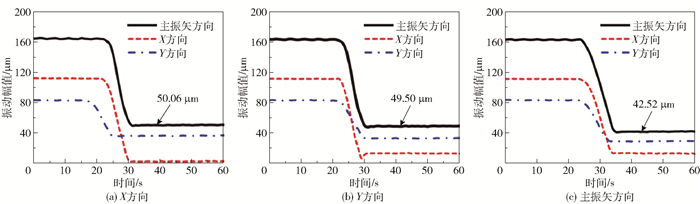
针对图 6(b)的重构结果,分别用X向、Y向和主振矢方向的振动矢量作为自动平衡的控制输入信号(对应轴心轨迹重构图中的Xmax、Ymax和Lmax),再进行相同状态下的自动平衡对比试验,每次试验均记录X、Y方向和主振矢方向的振动幅值。3次试验的结果见图 7。
|
图 7 3种控制输入条件下的自动平衡试验结果 Fig.7 Automatic balance test results for three control input conditions |
为更好地表征实际振动情况,采用系统平衡前后主振矢方向的振动幅值进行对比,结果见表 3。由图 7和表 3看出,以主振矢方向振动矢量作为自动平衡控制输入信号的平衡效果要优于其他两个方向。
| 下载CSV 表 3 3种控制输入响应主振矢方向自动平衡效果比较 Table 3 Comparison of the automatic balance effects of three control input responses |
(1) 仿真和试验结果均表明,当转子呈各向异性、支承刚度非线性时,自动平衡控制输入信号的方向对平衡效果影响很大,通过轴心轨迹重构方法可以获得最佳的控制输入信号。
(2) 当转子系统存在不平衡振动时,可通过互相垂直的双传感器信号重构轴心轨迹,获取基频轴心轨迹椭圆,得到表征系统振动的最大值—主振矢。
(3) 采用单向传感器信号或主振矢进行自动平衡控制,均能使系统不平衡振动大幅降低,但采用主振矢作为自动平衡控制输入信号可以得到更好的平衡效果。
| [1] |
李长河, 原所先, 修世超, 等. 超高速磨削中的砂轮自动平衡技术[J]. 新技术新工艺, 2004(5): 29-31. LI C H, YUAN S X, XIU S C, et al. Automatic balancing technology of grinding wheel in super-high speed grinding[J]. New Technology & New Process, 2004(5): 29-31. (in Chinese) |
| [2] |
GARITAONANDIA I, ALBIZURI J, HERNANDEZ-VAZQUEZ J M, et al. Redesign of an active system of vibration control in a centerless grinding machine:numerical simulation and practical implementation[J]. Precision Engineering, 2013, 37(3): 562-571. DOI:10.1016/j.precisioneng.2013.01.001 |
| [3] |
沈伟, 何立东, 高金吉. 应用电磁式主动平衡装置解决烟气轮机转子振动问题的研究[J]. 炼油技术与工程, 2005, 35(11): 25-30. SHEN W, HE L D, GAO J J. Reducing vibration of flue gas expander rotor with electromagnetic active balancing device[J]. Petroleum Refinery Engineering, 2005, 35(11): 25-30. (in Chinese) |
| [4] |
CHEN L F, CAO X, GAO J J. A study on electromagnetic driven bi-disc compensator for rotor auto-balancing and its movement control[J]. WSEAS Transactions on Systems and Control, 2010, 5(5): 333-342. |
| [5] |
张西宁, 刘旭, 吴婷婷. 注排液式砂轮在线动平衡技术研究[J]. 西安交通大学学报, 2017, 51(4): 1-5. ZHANG X N, LIU X, WU T T. Liquid injection and drainage online dynamic balancing technique for grinding wheel[J]. Journal of Xi'an Jiaotong University, 2017, 51(4): 1-5. (in Chinese) |
| [6] |
陈立芳, 陈哲超, 王维民, 等. 基于自适应粒子群优化的非稳态自动平衡控制算法研究[J]. 振动与冲击, 2018, 37(24): 131-136. CHEN L F, CHEN Z C, WANG W M, et al. Nonstationary autobalancing control based on adaptive particle swarm optimization[J]. Journal of Vibration and Shock, 2018, 37(24): 131-136. (in Chinese) |
| [7] |
潘纪根, 舒勤勤, 周礼彬. SBS全自动磨床砂轮在线动平衡系统在轧辊磨床的应用[J]. 宝钢技术, 1997(2): 10-12. PAN J G, SHU Q Q, ZHOU L B. Application of the on-line dynamic balance system for SBS fully autocontrolled grinding wheel in roll grinders[J]. Bao Steel Technology, 1997(2): 10-12. (in Chinese) |
| [8] |
陈立芳, 陈哲超.一种实现旋转机械在线自动平衡的剖分式自动平衡装置: CN106768642 A[P]. 2017-05-31. CHEN L F, CHEN Z C. Split automatic balancing device for realizing online automatic balance of rotating machinery: CN106768642 A[P]. 2017-05-31. (in Chinese) |
| [9] |
陈立芳, 吴海琦, 王维民, 等. 双配重平衡头无错调控制算法研究[J]. 北京化工大学学报(自然科学版), 2012, 39(2): 89-94. CHEN L F, WU H Q, WANG W M, et al. A study on error-free movement control algorithm for bi-disc balancer[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2012, 39(2): 89-94. (in Chinese) |
| [10] |
樊红卫, 景敏卿, 刘恒. 主动混合式砂轮-电主轴系统自动平衡装置研究综述[J]. 振动与冲击, 2012, 31(5): 26-30. FAN H W, JING M Q, LIU H. Review for studying on active hybrid auto-balancer of grinding wheel and motor spindle[J]. Journal of Vibration and Shock, 2012, 31(5): 26-30. (in Chinese) |
| [11] |
屈梁生, 邱海, 徐光华. 全息动平衡技术:原理与实践[J]. 中国机械工程, 1998, 9(1): 60-64. QU L S, QIU H, XU G H. Rotor balancing based on holo-spectrum analysis:principle and practice[J]. China Mechanical Engineering, 1998, 9(1): 60-64. (in Chinese) |
| [12] |
刘石, 屈梁生. 全息谱技术在轴系现场动平衡方法中应用[J]. 热能动力工程, 2009, 24(1): 24-30. LIU S, QU L S. A study of methods for an on-site shafting dynamic balance based on holographic spectrum technology[J]. Journal of Engineering for Thermal Energy and Power, 2009, 24(1): 24-30. (in Chinese) |
| [13] |
张立家, 韩捷. 全矢谱技术在旋转机械启停车中的分析研究[J]. 机械设计与制造, 2008(10): 106-108. ZHANG L J, HAN J. Study of vector spectrum technology in analyzing the starting-stopping process of rotary machine[J]. Machinery Design & Manufacture, 2008(10): 106-108. (in Chinese) |
| [14] |
朱东博.全矢谱技术及其在转子动平衡领域的应用研究[D].郑州: 郑州大学, 2012. ZHU D B. Research on the full vector spectrum theory and its application in dynamic balancing field[D]. Zhengzhou: Zhengzhou University, 2012. (in Chinese) |
| [15] |
雷文平.高速转子故障物理特性及全矢动平衡技术研究[D].郑州: 郑州大学, 2016. LEI W P. Research on fault physical charateristics and full vector dynamic balancing of high speed totors[D]. Zhengzhou: Zhengzhou University, 2016. (in Chinese) |
| [16] |
张文斌, 周晓军, 杨先勇, 等. 基于谐波窗方法的转子轴心轨迹提纯[J]. 振动与冲击, 2009, 28(8): 74-77. ZHANG W B, ZHOU X J, YANG X Y, et al. Harmonic window method for purification of axis trace[J]. Journal of Vibration and Shock, 2009, 28(8): 74-77. (in Chinese) |
| [17] |
JEONG H, PARK S, WOO S, et al. Rotating machinery diagnostics using deep learning on orbit plot images[J]. Procedia Manufacturing, 2016, 5: 1107-1118. |













