涡流管是一种结构简单、无运动构件的能量分离装置,因具有操作简单、工作性能安全稳定、冷热范围大、性价比高等特点而被广泛应用于化学、制冷、加工、真空、生物医学等诸多领域。
自涡流现象被发现以来,提高涡流管的制冷及制热性能就成为各国科学家研究的主题。尽管目前国内外对于涡流管内部能量分离机理还没有得到统一的结论,但这并不影响对涡流管内部工作性能的研究分析。龚迪澜等[1]通过实验分析分别从膨胀比、节流阀开度和进气温度的角度研究了涡流管的制冷和制热温度效应以及冷流率的变化规律,结果表明在相同的节流阀开度下,随着进气温度的升高,涡流管的制冷和制热温度效应、总制冷量均增大,而冷流率先升高后降低,进气温度每增加20 K,制冷温度效应平均增幅约为12%,制热温度效应平均增幅为5%。曹勇[2]通过实验对常温(288 K)和低温(240 K)下的冷流率、入口压力、工质种类等涡流管特性进行研究,发现常温和低温下涡流管的冷端温差和冷流率的变化趋势基本相同,但是在相同的入口压力、喷嘴等条件下,低温下的冷端温差比常温下的冷端温差大。Devade等[3]通过实验研究了冷孔直径、长径比和出口阀角度对涡流管制冷和制热性能的影响。Berber等[4]基于rule-based Mamdani-type fuzzy建模技术,通过实验研究了逆流涡流管的制冷和制热性能,发现冷流率的增加是由于冷气流质量流量的增加和热气流质量流量的减少。Sharma等[5]对涡流管数值分析研究的发展历程进行了系统的总结。Tyutyuma[6]基于涡流管平面旋流模型,采用实验与模拟对比方法,从理论上分析了管内热过程对涡流能量分离效率的影响。周少伟等[7]通过系统的实验方法研究了涡流管制冷效应、单位制冷量和绝热效率随切向入口压力与冷气流率两个特定因素的变化规律,并推导出相对制冷特性随冷气流率变化的经验公式。何曙等[8]通过实验研究了进气压力对涡流管性能的影响。何丽娟等[9]以理想CO2气体为工作流体,对涡流管的能量分离效应进行模拟,发现随着冷流率的增大,冷热流分界面逐渐增大,制冷温度效应呈先增大后减小的趋势。
对于涡流管而言,其工质主要来源于空压机或空气储罐。空压机运行时间的延长或空气储罐环境温度的变化会导致压缩空气温度产生波动,特别是在空气消耗量比较大的情况下,温度会产生较大幅度的波动,进而对涡流管的制冷性能造成明显影响。当前文献多采用理想涡流管模型,主要集中于对涡流管结构参数以及压力、介质等操作参数的研究,针对温度与冷流率改变对涡流管性能影响的研究相对较少,关于进气温度和冷流率对涡流管制冷性能的影响规律缺乏深入的理解,进而阻碍了涡流管的工业应用及结构设计。为此,本文选取更加宽泛的温度范围,研究温度与冷流率对涡流管性能的影响。采用基于工业应用的涡流管模型,就270~310 K温度范围内不同进气温度和冷流率对涡流管制冷性能的影响进行研究,以便掌握进气温度和冷流率这两种参量对制冷性能的影响规律,更好地指导涡流管的工程应用,并为涡流管设计提供一定的理论支撑。
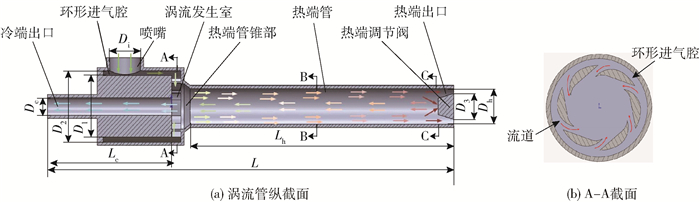
1 计算模型的建立 1.1 涡流管物理计算模型本文的研究对象结构基于NEX FLOWTM 50008H型涡流管,其结构如图 1所示。涡流管由喷嘴、环形进气腔、流道、涡流发生室、冷端管、热端管和热端调节阀7部分组成,其结构尺寸如下:涡流管总长L=130 mm,喷嘴直径Di=12 mm,环形进气腔内径D1=22 mm,外径D2=25 mm,流道沿涡流发生室切向分布,流道截面为矩形,边长B=1.8 mm,涡流发生室直径Dv=14 mm,冷端管径Dc=5.4 mm,冷端管长Lc=40 mm,热端管锥段锥度θh=26.6°,热端管径Dh=11 mm,热端管长Lh=85 mm, 热端调节阀为圆锥台,其大圆直径D3=8 mm, 小圆直径D4=5 mm,热端调节阀锥度θ=32°。
|
图 1 涡流管结构及尺寸参数 Fig.1 Structure and size parameters of the vortex tube |
由于涡流管内部流体的速度非常高且运动过程复杂,因此认为涡流管内部流体作湍流运动,且气体可压缩。Sinhamahapatra等[10]、李龙等[11-12]、Skye等[13]通过研究发现,Standard k-ε模型是一个半经验公式,适用范围广、经济且有合理的精度,适用于完全湍流的流动模拟,可以很好地反映涡流管内部流场的变化情况。因此本文采用Standard k-ε湍流模型,稳态流动条件下的雷诺应力项、湍动能方程和耗散率方程分别为
| $ - \rho \overline {u_i^\prime u_j^\prime } = {\mu _{\rm{t}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\left( {\rho k + {\mu _{\rm{i}}}\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right){{\rm{ \mathsf{ δ} }}_{ij}} $ | (1) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - \\ {Y_{\rm{M}}} + {S_k} \end{array} $ | (2) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_{\rm{k}}} + } \right.\\ \left. {{C_{3\varepsilon }}{G_{\rm{b}}}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } \end{array} $ | (3) |
式中,Gk为平均速度的梯度变化产生的湍动能项;Gb为由浮力影响产生的湍动能项;YM为在可压缩湍流中,过度耗散产生的波动;σk和σε分别表示与湍动能k和耗散率ε对应的Prandtl数;Sk、Sε分别为k、ε的源项;C1ε、C2ε、C3ε为经验常数;μt为湍流黏性系数。
本文选用Fluent软件进行数值模拟,所用流体为理想可压缩空气,比热cp=1 006.43 J/(kg·K),黏度μ=1.789 4×10-5 kg/(m·s),壁面光滑且无滑移,涡流管入口边界条件设为压力入口条件,pi=0.6 MPa(总压),冷热端出口边界条件均采用压力出口条件,其中冷端出口压力pc=0.1 MPa,热端出口为静压且可调,通过调节热端压力来改变冷流率。
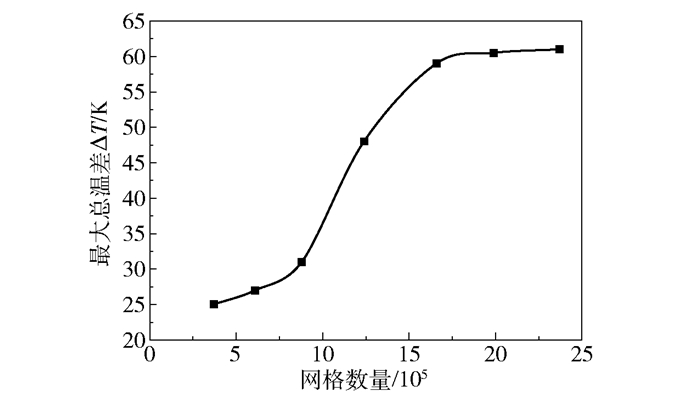
1.3 网格划分及网格无关性检验网格对于模型的计算结果有着很大的影响,本文模型采用非结构网格进行划分。为了消除网格数量对计算结果的影响,确定最佳的网格尺寸,在保持热端出口压力ph=0.32 MPa的条件下,得到了不同网格数量对最大总温差(相同条件下涡流管最低温度与最高温度的差值)的影响规律,如图 2所示。从图 2可以看出,随着网格数量的增加,最大总温差呈增大趋势,在网格数量达到15×105以上时,最大总温差变化趋势趋于平缓,继续加密网格达到相同的精度时所用时间较长。因此,本文最终选取网格数量为16×105,该网格数量下网格尺寸对于计算结果的影响可以忽略不计。
|
图 2 网格数量和最大总温差的关系 Fig.2 Relationship between grid node number and the maximum temperature difference |
为方便分析,对涡流管的性能参数进行定义,表达式分别如下。
| $ {\rm{制冷温度效应}}:\Delta {T_{\rm{c}}} = {T_{\rm{i}}} - {T_{\rm{c}}} $ | (4) |
| $ {\rm{制热温度效应}}:\Delta {T_{\rm{h}}} = {T_{\rm{h}}} - {T_{\rm{i}}} $ | (5) |
| $ {\rm{总温差}}:\Delta T = {T_{\rm{h}}} - {T_{\rm{c}}} $ | (6) |
| $ {\rm{冷流率 }}:m = \frac{{{Q_{\rm{c}}}}}{{{Q_{\rm{i}}}}} $ | (7) |
| $ {\rm{单位制冷量 }}:{q_{\rm{c}}} = m{c_p}\Delta {T_{\rm{c}}} $ | (8) |
| $ {\rm{制冷效率}}:\eta = \frac{{m{c_p}\Delta {T_{\rm{c}}}}}{{R{T_{\rm{i}}}\ln \left( {\frac{{{p_{\rm{i}}}}}{{{p_{\rm{c}}}}}} \right)}} \times 100\% $ | (9) |
式中,Ti、Tc、Th分别为涡流管入口、冷端出口、热端出口温度,K;Qi、Qc分别为涡流管入口、冷端出口质量流量,kg/s;cp为定压比热容(270~310 K范围内cp=1 006.43 J/(kg·K));pi、pc分别为入口、冷端出口压力,MPa;R为空气气体常数,R≈8.314 J/(mol·K)。
2.1 模拟可靠性的实验验证湍流模型的选择对于计算结果的准确性和可靠性具有很大的影响,为了确保所选用湍流模型的合理有效,对模拟结果进行了实验验证。
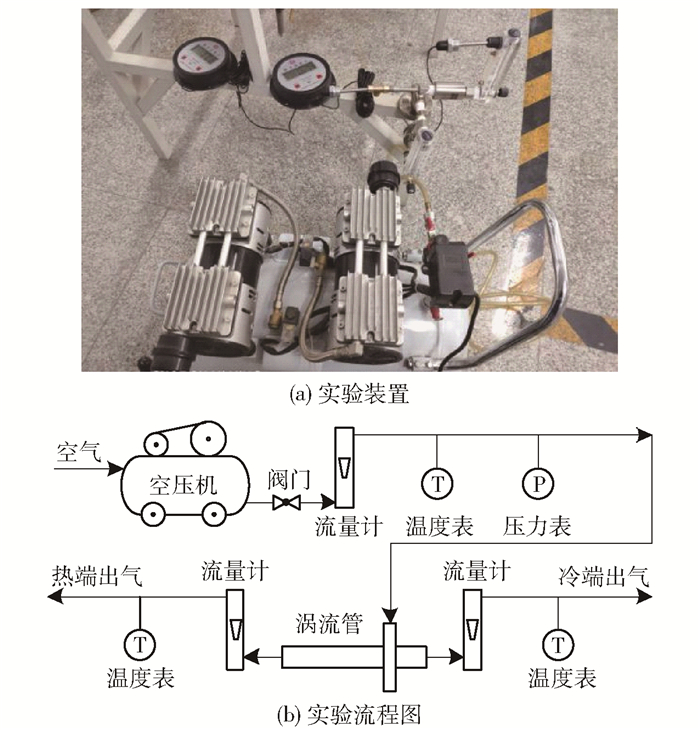
2.1.1 实验装置及流程图 3(a)为本文所用模型的实验装置,选用NEX FLOWTM 50008H型涡流管进行实验,采用空气压缩机作为供气源,通过改变热端调节阀开度、调节冷热比例,从而改变冷流率。
|
图 3 实验装置及实验流程图 Fig.3 Experimental setup and flow chart |
图 3(b)为实验流程图。空气经压缩机压缩后进入储罐,调节储罐稳压阀门使储罐中的压缩空气达到所需压力并保持稳定。由进气口转子流量计测量入口空气流量,在进气口转子流量计与涡流管之间管线上设置数显温度表和高精度压力表以测量涡流管进口气流的温度和压力。高压气流在涡流管中被分离成冷、热两股气流,在冷端和热端的出口分别设置转子流量计和数显温度表以测量相应出口气体的流量和温度。通过调节涡流管热端调节阀改变冷、热端出口流量,得出不同冷流率下的实验结果。
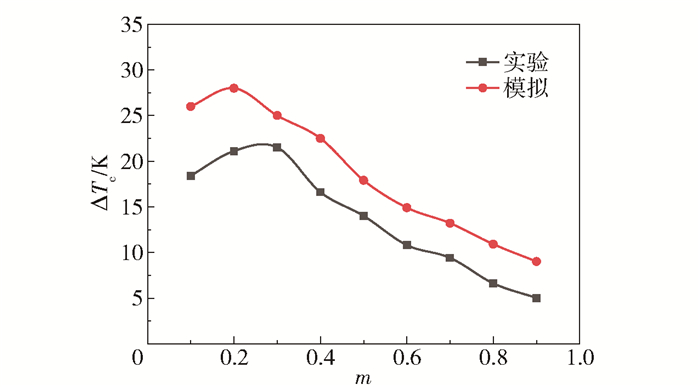
2.1.2 实验数据分析图 4是在进气温度为290 K、进气压力0.3 MPa(表压)条件下制冷温度效应随冷流率变化的实验结果及相同条件下的模拟结果曲线。从图 4可以看出,实验与模拟的制冷温度效应随冷流率的变化规律基本相同,两者的平均相对偏差为37.6%。部分冷流率下的相对偏差较大,是由于涡流管与连接管路无法做到与外部环境完全绝热,致使冷端出口温度测量值偏高,反映到图中就会出现部分数据偏差较大的现象。实验中制冷温度效应越大,误差对实验结果的影响就会越小。由于模拟结果和实验结果变化趋势相同,并且平均相对误差在可接受的范围内,可以认为本文的模拟方法和湍流模型是正确可靠的。
|
图 4 制冷温度效应随冷流率的变化曲线(290 K) Fig.4 Variation in cooling effect as a function of cold flow rate (290 K) |
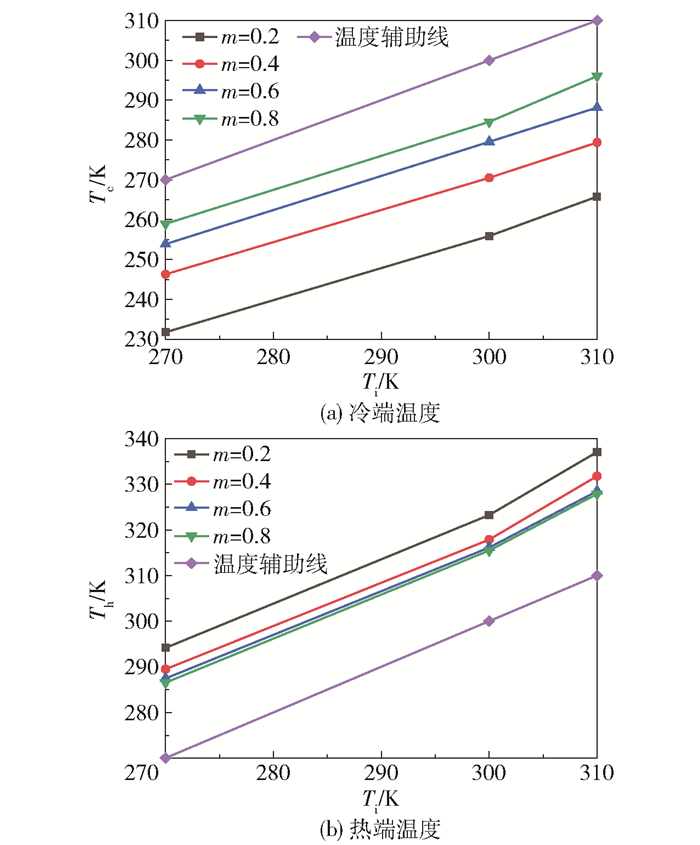
涡流管冷端温度、热端温度与进气温度的差值代表了涡流管的能量分离效果。当冷端和热端出口温度与进气温度相同时,涡流管就失去了能量分离作用。为了便于直观分析进气温度对涡流管冷端和热端温度的影响,本文提出了温度辅助线概念,该辅助线上任意一点的冷端温度或热端温度与进气温度相同。温度辅助线与实际的冷端或热端温度线的偏差程度代表了涡流管的能量分离能力。
图 5(a)是不同冷流率下涡流管冷端温度随进气温度的变化曲线。从图中可以看出,随着进气温度的升高,冷端出口温度基本上按照线性规律同步升高;不同的冷流率下冷端出口温度随进气温度的变化趋势基本相同;随着进气温度的升高,制冷温度效应也相应增大,但增大幅度较小。
|
图 5 涡流管冷、热端温度随进气温度的变化曲线 Fig.5 Variation of the temperatures at the cold and hot ends of the vortex tube as a function of the inlet temperature |
图 5(b)是不同冷流率下涡流管热端温度随进气温度的变化曲线。与图 5(a)对比发现它们的曲线变化趋势基本相同:随着进气温度的升高,热端出口温度基本上按照线性规律同步升高;不同的冷流率下热端出口温度随进气温度的变化趋势基本相同;随着进气温度的升高,制热温度效应也相应增大,但增大幅度较小。
由图 5(a)和(b)的对比可知,进气温度的升高会导致涡流管冷端及热端温度同步上升,并且进气、冷端和热端温度增幅也基本相同。这种现象说明,随着进气温度的升高,进入到涡流管内的气体热能增加,在没有外部做功及绝热状态下,涡流管内总能量的增加量就是热能的增加量。涡流管内的总能量除了气体热能外,还包括气体动能和气体势能,动能和势能的相互转化引起涡流管中心区域和周边区域温度产生差别,这种温度降低或升高的幅度是相对而言的,与其基础温度即进气温度绝对值关系不大,所以会产生冷端和热端温度随进气温度同步上升的结果。
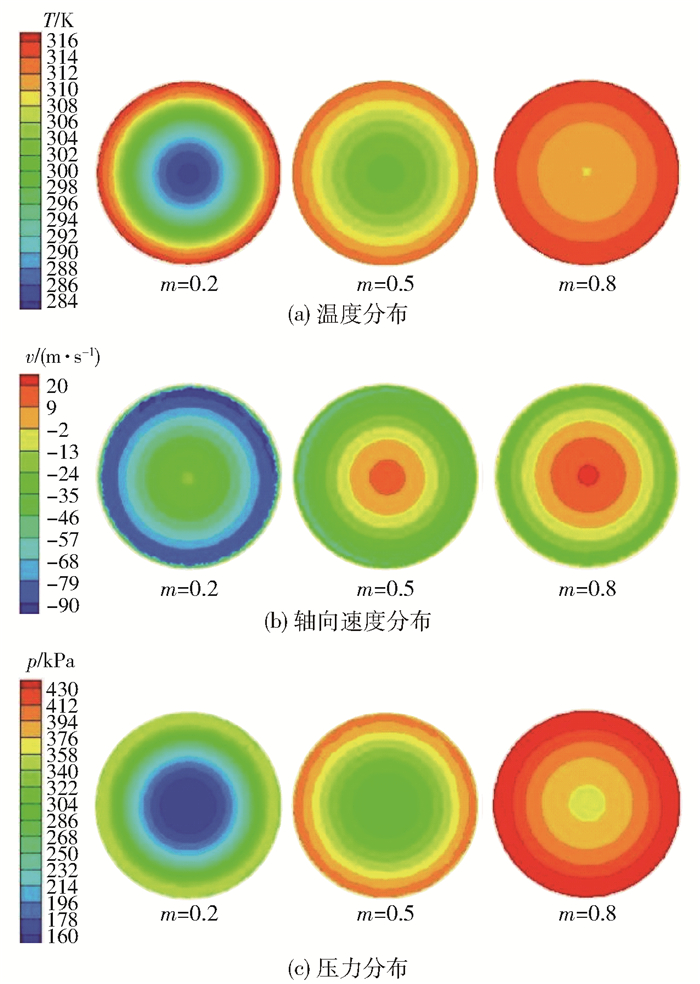
图 6是在进气温度Ti=300 K的条件下,图 1中B-B截面处的温度、轴向速度以及压力分布云图,其中冷端方向为正。
|
图 6 B-B截面温度、轴向速度及压力分布云图 Fig.6 Temperature, axial velocity and pressure distribution nephograms of the B-B section |
从图 6可以看出,随着冷流率的逐渐增大,热端管中气流温度逐渐升高,热端管中心区域与外部区域的温差逐渐减小;热端管中沿管壁向热端调节阀方向流动的气流速度逐渐减小,而沿轴线向冷端出口方向流动的气流速度逐渐增大;热端管中心区域与周边区域的压力差逐渐减小。分析以上现象认为:冷流率改变的原因是涡流管内的压力场发生了变化,随着热端压力逐渐增大,冷流率也会逐渐增大,使沿管壁流向热端调节阀的气流运动受阻;热端压力越大,冷流率越高,流向热端管的气流流速越低,气流具有的动能越小,由气体动能和势能相互转化引起的热端管中心和周边区域的温度分离效果越差,热端管中的能量分离效果也相应越差。根据能量守恒定律,中心区域气流的温度会随冷流率的增大而增大,热端管中的气流温差随冷流率的增大而减小。同时,由于冷热端压力差的影响,热端中心区域的气流从高压流向低压也会使得速度增大。
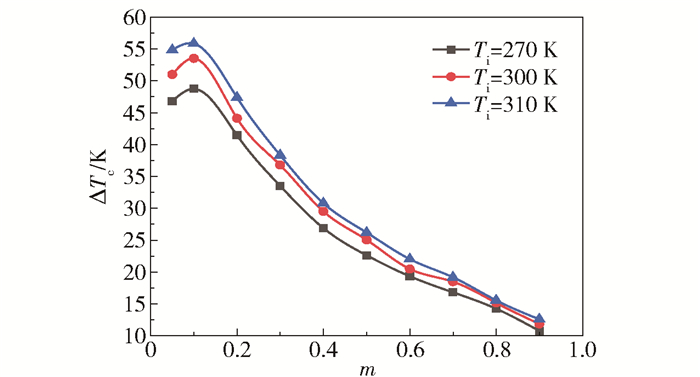
2.3 冷流率对涡流管制冷性能的影响图 7是不同进气温度时,制冷温度效应ΔTc随冷流率m的变化曲线。分析此特性曲线可以看出:涡流管制冷温度效应随进气温度的增加而增大,且随着冷流率的增大,进气温度对涡流管制冷温度效应的影响在逐渐减小。在同一进气温度条件下,涡流管的制冷温度效应ΔTc先随冷流率m的增大而增大,在冷流率为0.1~0.2时达到峰值,之后随冷流率的增大而迅速下降,且随冷流率的增大,特性曲线的下降速度逐渐降低。以上现象说明,在同一进气温度条件下,存在一最优冷流率使涡流管的制冷温度效应达到最大值。
|
图 7 冷流率对制冷温度效应的影响 Fig.7 Effect of cold flow rate on cooling effect |
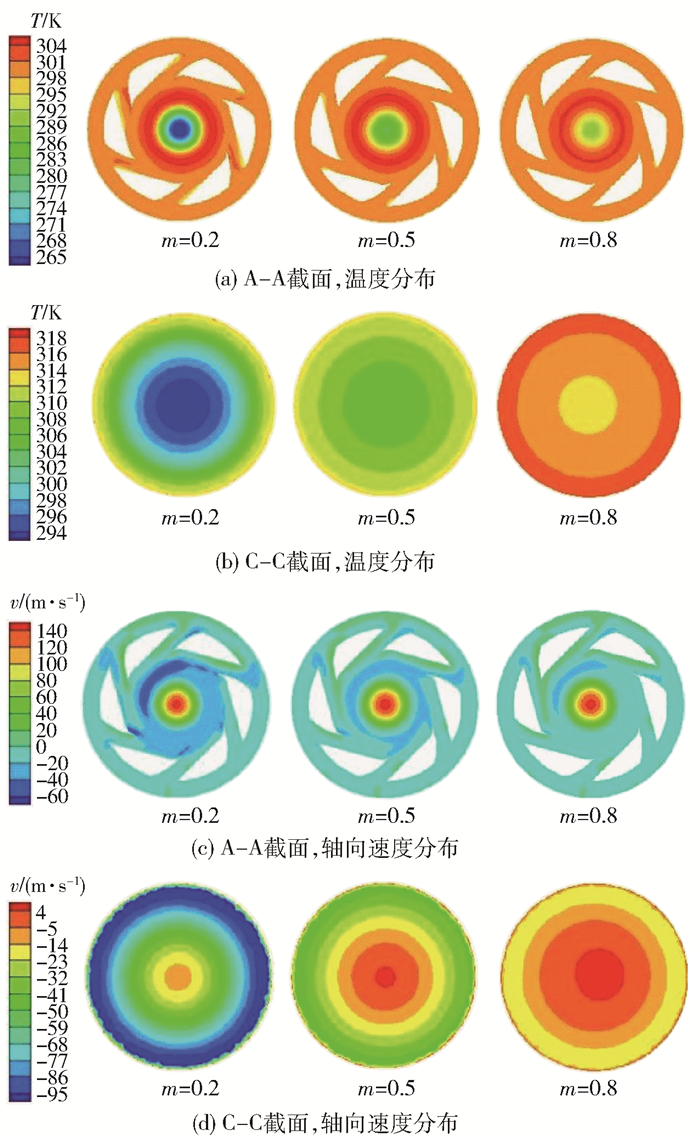
图 8是在进气温度Ti=300 K的条件下,图 1中A-A、C-C截面处的温度及轴向速度分布云图,其中冷端方向为正。从图 8可以看出,气流在环形进气腔及流道中的温度基本不随冷流率的变化而变化;随着冷流率的增大,涡流室中心处的温度逐渐升高;热端管中的气流温度逐渐升高,冷热气流区分逐渐不明显;从涡流室流向热端调节阀的气流速度逐渐减小,热端管中沿轴线流向冷端的气流速度逐渐增大。
|
图 8 A-A和C-C截面的温度及轴向速度分布云图 Fig.8 Temperature and axial velocity distribution nephograms of the A-A and C-C sections |
图 9为进气温度Ti=300 K,冷流率m=0.5的条件下,涡流管纵截面的速度流线图。从图 9可以很明显地看出,高压气体进入涡流室后,一部分气流沿管壁流向热端管,一部分气流直接流入冷端管。

|
图 9 纵截面速度流线图 Fig.9 Streamline diagram of the longitudinal section velocity |
形成上述温度分布的原因是高压气体进入喷嘴后膨胀使得其速度增大,在经过流道后以一定的角度进入涡流室并形成自由涡,其中绝大多数的气流沿涡流管内壁旋转流向热端管,在到达热端调节阀处时一部分气流从热端出口流出,另一部分气流经调节阀反弹沿轴线流向冷端管,极少量的气流直接流入冷端管。在保持进气压力不变的情况下,热端压力增大,迫使热端管内更多的气流沿轴线流向冷端管,涡流管内的能量分离效果增大,同时也迫使更多的气流直接从涡流室流入冷端管,使流入热端管内的气流减少,涡流管内的能量分离效果降低。
当热端压力较小时,涡流管内分离效果的降低量小于其升高量,即由于摩擦等因素使流体速度下降导致的分离效果降低量小于由于冷热流体之间的能量转化导致的分离效果升高量,因此涡流管的制冷温度效应呈上升趋势;随着热端压力逐渐增大,冷流率逐渐增加,涡流管内能量分离效果的减少量逐渐等于其增加量,此时涡流管的制冷温度效应达到峰值,此时的冷流率即为最优冷流率;继续增大热端压力,涡流管内能量分离效果的减少量将大于其增加量,涡流管的制冷温度效应呈下降趋势。当热端压力较大时,涡流管内大部分的气流直接流入冷端管,继续增大热端压力,提高冷流率,涡流管内的能量分离已经不明显,同时,随着冷流率的增大,冷热端温差逐渐减小,涡流管制冷温度效应的下降趋势逐渐减小。
改变进气温度时,涡流管中气体的运动状态会发生改变,涡流管的制冷及制热温度效应也随之改变。分析图 7发现,在同一入口压力条件下,涡流管的最优冷流率不随进气温度的改变而改变。我们认为,最优冷流率与涡流管的工作参数无关。通过与Devade等[3]、周少伟等[7]、申江等[14]的研究结果对比发现,这些文献中涡流管的最优冷流率同样不随入口压力的改变而改变,只有在结构参数改变时,涡流管的最优冷流率才会发生改变。因此可以得出结论:当结构参数确定时,涡流管的最优冷流率不因工作参数的改变而改变。
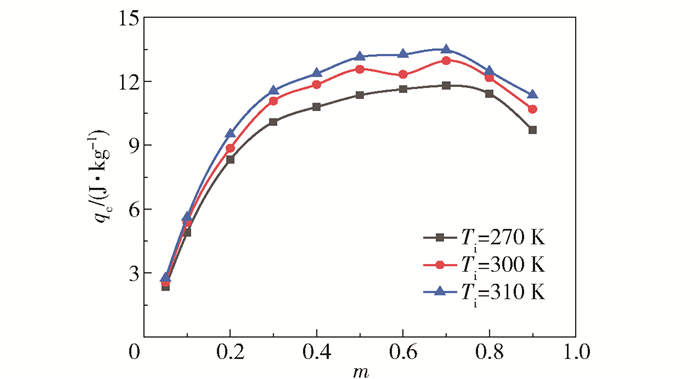
图 10和图 11分别为不同进气温度下涡流管单位制冷量qc和制冷效率η随冷流率的变化曲线。从图 10可以看到,在相同冷流率下,当进气温度升高时,涡流管的单位制冷量也随之增大。这是因为涡流管的单位制冷量与制冷温度效应有关,随着进气温度的升高,涡流管的制冷温度效应增大,其单位制冷量也随之增大。
|
图 10 单位制冷量随冷流率的变化曲线 Fig.10 Variation in unit cooling capacity with changing cold flow rate |
|
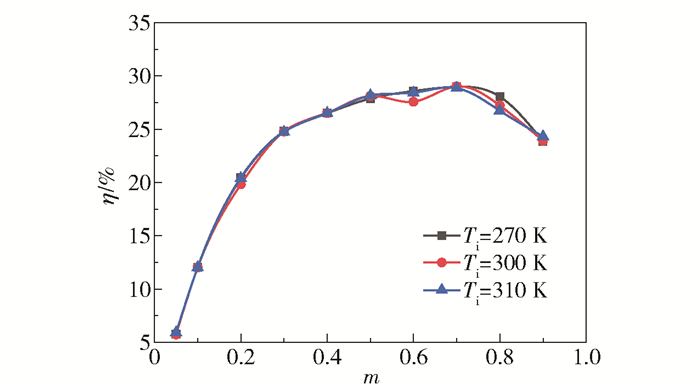
图 11 制冷效率随冷流率的变化曲线 Fig.11 Variation in cooling efficiency with changing cold flow rate |
图 10还显示,涡流管的单位制冷量随冷流率的增大呈先增大后减小的趋势。在冷流率为0.05~0.2时单位制冷量随冷流率的增大而增大的幅度最强;在冷流率为0.6~0.8附近时达到最大单位制冷量。根据单位制冷量计算公式可知,影响涡流管单位制冷量的因素是冷流率和制冷温度效应,从图 7可以看到,随着冷流率的增大,涡流管的制冷温度效应先增大后减小,冷流率与制冷温度效应的乘积也随之增大,当冷流率达到0.7左右时,其乘积达到最大值,然后逐渐减小。因此,存在一最优冷流率使得涡流管的单位制冷量达到最大值。
从图 11可以看出,冷流率对涡流管制冷效率和单位制冷量的影响规律相似,并且涡流管的制冷效率基本上不随进气温度的改变而改变。在冷流率为0.5~0.7时涡流管的制冷效率最高,且最大制冷效率可以达到29.02%。
图 10和图 11的曲线具有相似性。分析制冷效率公式可知,涡流管的制冷效率受单位制冷量和进气温度比值的影响,随着进气温度的升高,涡流管的单位制冷量也随之增大,但增大的幅度较小,单位制冷量和进气温度的比值变化较小,因此涡流管的制冷效率不随进气温度的改变而改变。
根据以上结果可知,涡流管的制冷及制热温度效应是冷流率的独立函数。从图 10可以看出,单位制冷量随冷流率变化曲线的趋势基本不受进气温度的影响。因此可以得出结论,当涡流管的结构参数确定时,涡流管的制冷效率不会随其操作参数的改变而发生变化。
3 结论(1) 在同一冷流率下,涡流管的冷端出口温度、热端出口温度、制冷温度效应及单位制冷量均随进气温度的升高而增大,而制冷效率基本不受进气温度的影响。
(2) 在不同温度下,涡流管的制冷温度效应、单位制冷量及制冷效率都随冷流率的增大呈先增大后减小的趋势。
(3) 在不同温度下,冷流率存在一最佳范围使得此范围内的涡流管制冷温度效应、单位制冷量及制冷温度效应的值最大,但各个涡流管对应的冷流率范围不同,且此范围基本不受进气温度的影响。
| [1] |
龚迪澜, 毛军逵, 邓明, 等. 进气温度与压力对涡流管性能影响的实验[J]. 航空动力学报, 2017, 32(3): 599-606. GONG D L, MAO J K, DENG M, et al. Experiment on influences of inlet temperature and pressure on vortex tube's performance[J]. Journal of Aerospace Power, 2017, 32(3): 599-606. (in Chinese) |
| [2] |
曹勇.小流量涡流管特性的理论与实验研究[D].杭州: 浙江大学, 2003. CAO Y. The oretical and experimental study on the performance of a small flow vortex tube[D]. Hangzhou: Zhejiang University, 2003. (in Chinese) |
| [3] |
DEVADE K D, PISE A T. Exergy analysis of a counter fow Ranque-Hilsch vortex tube for different cold orifice diameters, L/D ratios and exit valve angles[J]. Heat Mass Transfer, 2017, 53: 2017-2029. DOI:10.1007/s00231-016-1962-7 |
| [4] |
BERBER A, DINCER K, YILMAZ Y, et al. Rule-based Mamdani-type fuzzy modeling of heating and cooling performances of counter-flow Ranque-Hilsch vortex tubes with different geometric construction for steel[J]. Energy, 2013, 51: 297-304. DOI:10.1016/j.energy.2013.01.005 |
| [5] |
SHARMA T K, RAO G A P, MURTHY K M. Numerical analysis of a vortex tube:a review[J]. Arch Computat Methods Eng, 2017, 24(2): 251-280. DOI:10.1007/s11831-016-9166-3 |
| [6] |
TYUTYUMA V D. Influence of thermal processes on the efficiency of the energy separation in a Ranque vortex tube[J]. Journal of Engineering Physics and Thermophysics, 2016, 89(6): 1505-1513. DOI:10.1007/s10891-016-1520-7 |
| [7] |
周少伟, 姜任秋, 宋福元, 等. 入口压力与冷气流率对涡流管制冷性能影响研究[J]. 应用基础与工程科学学报, 2006, 14(4): 543-549. ZHOU S W, JIANG R Q, SONG F Y, et al. Experimental investigations into the influences of inlet pressure and cold air fraction on the refrigerating performance of a vortex tube[J]. Journal of Basic Science and Engineering, 2006, 14(4): 543-549. (in Chinese) DOI:10.3969/j.issn.1005-0930.2006.04.012 |
| [8] |
何曙, 吴玉庭, 郭建, 等. 进口压力对涡流管性能影响的实验研究[J]. 空气动力学学报, 2006, 24(4): 487-490. HE S, WU Y T, GUO J, et al. Experimental study on the effect of the inlet pressure on the performance of vortex tube[J]. Acta Aerodynamica Sinica, 2006, 24(4): 487-490. (in Chinese) DOI:10.3969/j.issn.0258-1825.2006.04.017 |
| [9] |
何丽娟, 马文清, 孙尚志, 等. 冷孔板直径与冷流率对涡流管流场的影响[J]. 低温工程, 2019(2): 6-11. HE L J, MA W Q, SUN S Z, et al. Effect of cold orifice diameter and cold flow rate on vortex tube field[J]. Cryogenics, 2019(2): 6-11. (in Chinese) |
| [10] |
DUTTA T, SINHAMAHAPATRA K P, BANDYOPDHYAY S S. Comparison of different turbulence models in predicting the temperature separation in a Ranque-Hilsch vortex tube[J]. International Journal of Refrigeration, 2010, 33(4): 783-792. DOI:10.1016/j.ijrefrig.2009.12.014 |
| [11] |
李龙.小管径涡流管三维数值模拟及制冷性能研究[D].西安: 西安理工大学, 2014. LI L. The study of three-dimensional numerical simulation and refrigeration performance of the small diameter vortex tube[D]. Xi'an: Xi'an University of Technology, 2014. (in Chinese) |
| [12] |
李龙, 李言, 何望云. 涡流室结构参数对小管径涡流管制冷性能影响的三维数值模拟[J]. 应用基础与工程科学学报, 2016, 24(3): 528-539. LI L, LI Y, HE W Y. Effect of swirl chamber structure parameters on refrigeration performance for small diameter vortex tube by 3D numerical simulation[J]. Journal of Basic Science and Engineering, 2016, 24(3): 528-539. (in Chinese) |
| [13] |
SKYE H M, NELLIS G F, KLEIN S A. Comparison of CFD analysis to empirical data in a commercial vortex tube[J]. International Journal of Refrigeration, 2006, 29(1): 71-80. DOI:10.1016/j.ijrefrig.2005.05.004 |
| [14] |
申江, 边煜竣, 郭欣炜. 冷端孔径对涡流管性能影响的实验研究[J]. 制冷学报, 2017, 38(6): 87-93. SHEN J, BIAN Y J, GUO X W. Experimental study on the effect of cold-end aperture on the performance of vortex tube[J]. Journal of Refrigeration, 2017, 38(6): 87-93. (in Chinese) DOI:10.3969/j.issn.0253-4339.2017.06.087 |







