稠油根据其特点可分为普通稠油(50 ℃,100~1 000 mPa·s)、特稠油(50 ℃,10 000~50 000 mPa·s)和超稠油(50 ℃,≥50 000 mPa·s)。随着稠油开采量的逐年增加,稠油管道运输备受关注,而稠油的物理特性及流动状态对管道的影响逐渐成为研究的热点。
国内外学者在稠油流态、特性等方面进行了大量的研究,如岳湘安等[1]运用控制变量法得到非牛顿流体在管道内产生的涡旋结构与流变指数有关的重要结论;Liepsch等[2]通过实验对非牛顿流体进行管内速度测定,得到流体无量纲的速度分布;顾效源等[3]通过模拟90°弯管内稠油的流动状态,得出了弯径比的改变会导致迪恩涡结构发生变化,进而影响稠油局部阻力及剪切速率的重要结论;刘新锋等[4]就不同类型的筛管内含砂稠油对管壁造成冲蚀效果的影响因素进行分析,得到了降低流速及改变筛管结构可有效减缓冲蚀作用的结论;朱辉等[5]对90°弯管内流体的二次流动进行分析,得到了不同角度截面二次涡形态随雷诺数Re变化的规律;偶国富等[6]利用计算流体力学(computational fluid dynamics,CFD)软件,运用流固耦合分析方法对弯管的冲蚀现象及失效趋势进行了分析和研究;邓智强等[7]探究了温度变化对弯头平均冲蚀速率的影响规律,得出在60 ℃工况下弯头平均冲蚀速率降至最低值,该结论对缓解原油输运管路运行过程中的冲蚀现象具有一定指导意义;王博等[8]运用CFD分析软件对含砂原油管道颗粒的属性对弯头处的冲蚀磨损问题进行了研究,通过改变入口流速、颗粒质量流率、颗粒直径等条件,得到了冲蚀速率的变化规律。
综合以上文献可知,以往对于冲蚀问题的研究主要以含砂天然气或含砂原油为研究对象,对重质稠油的冲蚀问题涉及较少。为研究不同的温度、砂粒粒径及质量流率对重质稠油冲蚀作用的影响,运用ANSYS数值模拟软件,对重质稠油输送管道90°弯管内的冲蚀现象进行分析,明确砂石颗粒对管道内壁造成冲蚀的机理和变化规律。
1 数学模型 1.1 湍流模型通过计算可知,模拟流态为湍流(Re=3 840),因此选取Realizable k-ε湍流模型进行计算,具体模型为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{{\partial \left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right]}}{{\partial {x_j}}} + {G_{\rm{k}}} + \\ {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} + {S_k} \end{array} $ | (1) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{{\partial \left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right]}}{{\partial {x_j}}} + {C_{1\varepsilon }}\frac{\varepsilon }{k} \cdot \\ {G_{\rm{k}}} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_{\rm{b}}} - \rho {C_{2\varepsilon }}\frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } \end{array} $ | (2) |
其中
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_{\rm{k}}} = {\mu _{\rm{t}}}\left\{ {2\left[ {{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2}} \right] + } \right.\\ \left. {{{\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}^2}} \right\} \end{array} $ | (3) |
式中,ρ为流体密度,kg/m3;k为湍动能,m2/s2;ε为湍动能耗散率,J/(kg·s);μ为湍流黏度,Pa·s;Gk为速度梯度引起的湍动能附加项;Gb为浮力引起的湍动能附加项;YM为湍流脉冲的扩张项;C1ε、C2ε和C3ε为经验常数;σk和σε分别是湍动能及湍动能耗散率的普朗特数;μt为湍动黏度,Pa·s;Sk、Sε为k和ε的源项;u、v、w为流体流速在三维方向的分量,m/s;重质稠油可认为是不可压缩流体,因此取Gb=0、YM=0、Sk=0、Sε=0、C1ε=1.44、C2ε=1.92、C3ε=0、σε=1.3、σk=1.0。
1.2 离散相模型根据牛顿第二定律,单位质量固体颗粒在气动阻力作用下的运动方程为
| $ \frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}t}} = {F_{\rm{D}}}\left( {u - {u_{\rm{p}}}} \right) + \frac{{g\left( {{\rho _{\rm{p}}} - \rho } \right)}}{{{\rho _{\rm{p}}}}} + F $ | (4) |
其中
| $ {{F_{\rm{D}}} = \frac{{18\mu }}{{{\rho _{\rm{p}}}d_{\rm{p}}^2}} \cdot \frac{{{C_{\rm{D}}}Re}}{{24}}} $ | (5) |
| $ {Re \equiv \frac{{\rho {d_{\rm{p}}}\left| {{u_{\rm{p}}} - u} \right|}}{\mu }} $ | (6) |
式中,F为单位质量砂粒所受到的正向应力,N;FD为单位质量砂粒所受到的流动阻力,N;CD为曳力系数;up为砂粒速度,m/s;ρp为砂粒密度,kg/m3;dp为砂粒粒径,mm。
1.3 离散相冲蚀模型(DPM)由于砂粒与弯管内壁面的非弹性碰撞会造成动能损失,从而使反弹角度发生变化。为了得到较准确的颗粒运动路径,采用Forder等[9]提出的壁面恢复系数法进行定义,法向及切向恢复系数如下。
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{\rm{N}}} = 0.988 - 0.780\alpha + 0.190{\alpha ^2} - 0.024{\alpha ^3} + }\\ \ \ \ \ \ \ \ \ {0.027{\alpha ^4}}\\ {{e_{\rm{T}}} = 1.000 - 0.078\alpha + 0.840{\alpha ^2} - 0.210{\alpha ^3} + }\\ \ \ \ \ \ \ \ \ {0.028{\alpha ^4} - 0.022{\alpha ^5}} \end{array}} \right. $ | (7) |
式中,α为砂粒与壁面的冲击角,rad;eN为法向恢复系数;eT为切向恢复系数。
管道壁面冲蚀速率计算公式如下。
| $ {Q_{{\rm{erosion }}}} = \sum\limits_{p = 1}^{{N_{{\rm{particles }}}}} {\frac{{{m_{\rm{p}}}C\left( {{d_{\rm{p}}}} \right)f(\alpha ){v^{b(v)}}}}{{{A_{{\rm{face }}}}}}} $ | (8) |
式中,Qerosion为冲蚀速率,kg/(m2·s);mp为颗粒质量流率,kg/s;C(dp)为砂粒粒径函数,取1.8×10-9;v为砂粒相对速度,m/s;b(v)为砂粒相对速度的函数,取2.6;Aface为壁面面积,m2;f(α)为冲击角函数,弯管的冲击角函数可用分段多项式函数拟合得到,即
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\alpha ) = \\ \left\{ {\begin{array}{*{20}{l}} {0 + 22.7\alpha - 38.4{\alpha ^2}, }&{\alpha \le 0.267{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rad}}}\\ {2.00 + 6.80\alpha - 7.50{\alpha ^2} + 2.25{\alpha ^3}, }&{\alpha > 0.267{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rad}}} \end{array}} \right. \end{array} $ | (9) |
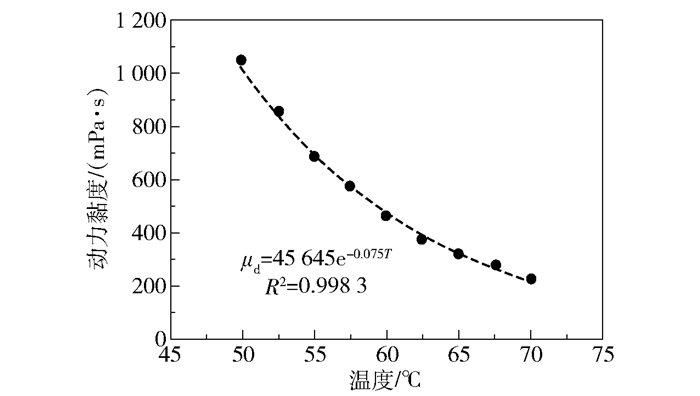
设定温度为50 ℃,动力黏度μd=1.112 Pa·s,密度ρ=960 kg/m3的某重质含砂稠油为输送介质,重力加速度g=9.8 m/s2,砂粒密度ρp=1 500 kg/m3,经拟合得到其黏温关系曲线[10]如图 1所示。
|
图 1 稠油黏度随温度变化曲线 Fig.1 Viscosity of heavy oil as a function of temperature |
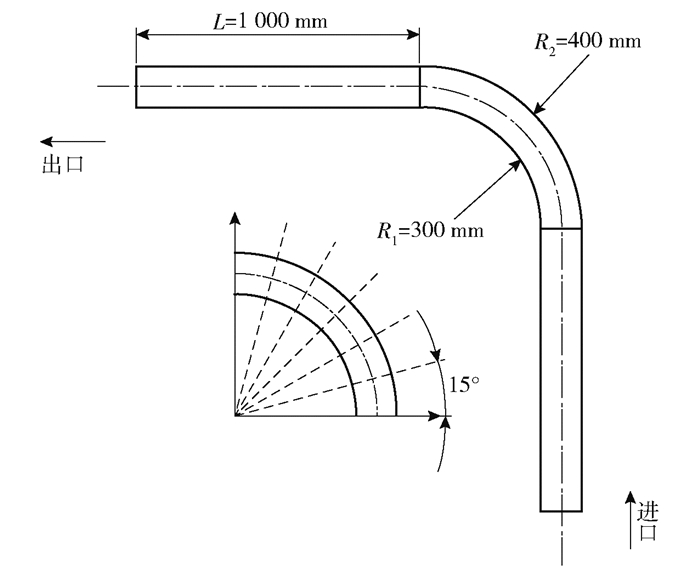
设定管道内径D=100 mm,壁厚δ=4 mm;为保证充分流动,设置进出口管段长度为10D,几何模型如图 2所示。
|
图 2 几何模型 Fig.2 Geometric model |
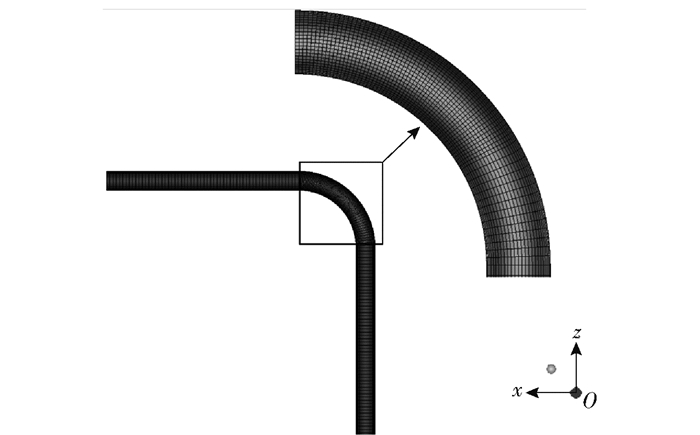
用Integrated Computer Engineering and Manufacturing (ICEM)对流动区域进行网格划分,设置7层边界层;为提高网格划分质量,对管道圆形截面进行“O”型剖分,对弯管25°~70°区域进行双重加密;经检验网格满足无关性要求,网格划分结果如图 3所示。
|
图 3 网格划分 Fig.3 Meshing |
由于输送介质温度较高,计算设置需考虑热浮力对砂粒运动轨迹的影响,因此稠油内部及管道壁面的剪切力、Saffman升力不可忽略[11-12];不考虑砂粒在壁面处的沉积增厚及腐蚀作用;湍动能及湍动能耗散率离散格式均采用二阶迎风格式、SIMPLEC算法进行运算。模型的边界设置如表 1所示。
| 下载CSV 表 1 边界条件 Table 1 Boundary conditions |
根据该种重质稠油的黏温曲线,分别对50~70 ℃(分度值2 ℃)条件下,流动状态相同(Re=3 840)的湍流冲蚀现象进行分析,并以50、60、70 ℃为例进行结果展示。
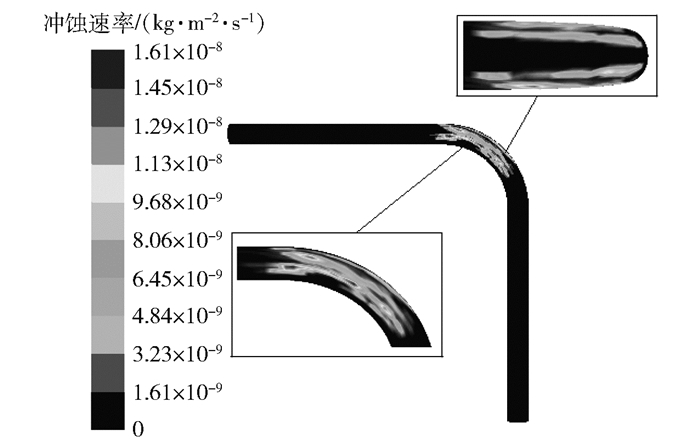
3.1.1 不同温度下的湍流冲蚀现象在温度50 ℃,砂粒粒径0.1 mm,质量流率0.01 kg/s的条件下,冲蚀速率云图如图 4所示。
|
图 4 T=50 ℃的稠油冲蚀速率云图 Fig.4 Cloud diagram of heavy oil erosion rate at T=50 ℃ |
由图 4可知,该条件下的稠油冲蚀区域主要集中于弯管侧壁面25°~90°范围内,且在弯管40°、60°及90°处均存在明显的冲蚀集中区域;弯管内拱面区未发生冲蚀现象,这是由于流体充分流动后,其在入口直管段与弯管段交界区域形成了流速较慢的稠油层,该稠油层对管壁起到了一定的保护作用;流经中心区的流体逐渐向两侧流动,且在弯管40°的侧壁面形成第一个冲蚀集中区域,在黏弹力及剪切力的作用下[13],砂粒随稠油在侧壁面滑移运动;外拱壁面冲蚀区域处的主流区出现脉冲径向增压,使得弯管60°侧壁面处出现第二个冲蚀集中区域,在此影响下,最大冲蚀速率出现在弯管90°方向线与侧壁面中线的交汇处[14],最大冲蚀速率为1.61×10-8 kg/(m2·s);外拱面冲蚀区域呈现条形分布,并随弯管角度的增加向侧壁面延伸,延伸区尽头处冲蚀速率达到最大,其中心区域未发生冲蚀,这是由于外拱壁面稠油层的分流作用,使外拱壁面中心区不受冲蚀影响。
在温度60 ℃,砂粒粒径0.1 mm,质量流率0.01 kg/s的条件下,冲蚀速率云图如图 5所示。
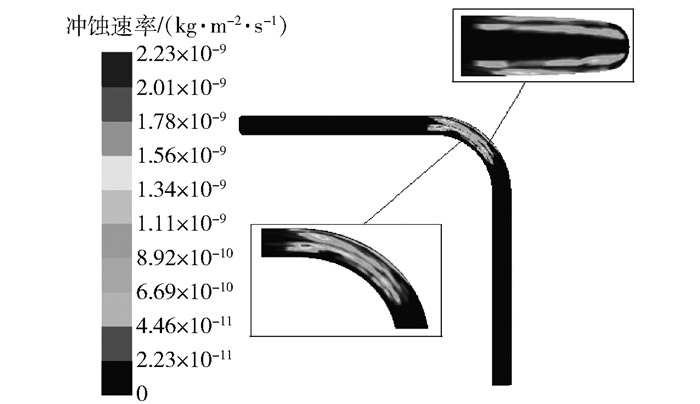
|
图 5 T=60 ℃时的稠油冲蚀速率 Fig.5 Cloud diagram of heavy oil erosion rate at T=60 ℃ |
由图 5可知,该条件下的稠油冲蚀区域与T=50 ℃的冲蚀区域近似相同,但最大冲蚀速率由1.61×10-8 kg/(m2·s)下降到2.23×10-9 kg/(m2·s)。砂粒在弯管60°处的冲蚀区域缩小并向90°方向移动,且在弯管40°方向的上侧壁面中心处的冲蚀区域也会缩小且冲蚀速率有所下降;弯管45°方向的外拱壁面出现新的冲蚀集中区域。这是由于温度上升,稠油黏度下降,流体热浮力对砂粒运动的影响加剧[15],因此砂粒向外拱壁面偏移,冲蚀区域沿流体流动方向逐渐下移。
在温度70 ℃,砂粒粒径0.1 mm,质量流率0.01 kg/s的条件下,冲蚀速率云图如图 6所示。
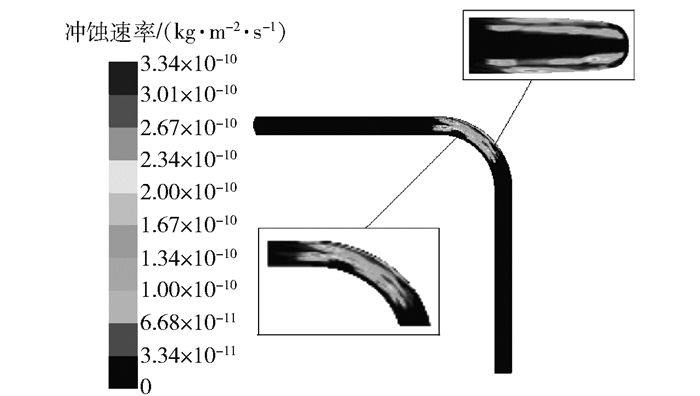
|
图 6 T=70 ℃时的稠油冲蚀速率 Fig.6 Cloud diagram of heavy oil erosion rate at T=70 ℃ |
由图 6可知,该条件下的稠油冲蚀速率相较于T=60 ℃时继续下降,但冲蚀区域位置变化却不明显;流体在弯管60°方向形成了新的冲蚀集中区域,外拱壁面条形冲蚀区域45°方向上的冲蚀集中区有所扩大,条形区末端的冲蚀区面积随温度变化较小,但冲蚀速率均显著下降,这主要是由于温度及流速的增加会使得稠油本身的黏性力对其束缚减小,砂粒在主流介质的携带下向管道中心线靠拢,因此减缓了砂粒对壁面的冲蚀作用,外拱壁面附近油层的保护作用受温度影响变化缓慢[16],但流体动能的增加使得冲蚀区域的面积有所扩大。
3.1.2 温度与冲蚀速率的关系根据模拟结果可知,冲蚀速率随稠油温度的变化关系及拟合曲线如图 7所示。
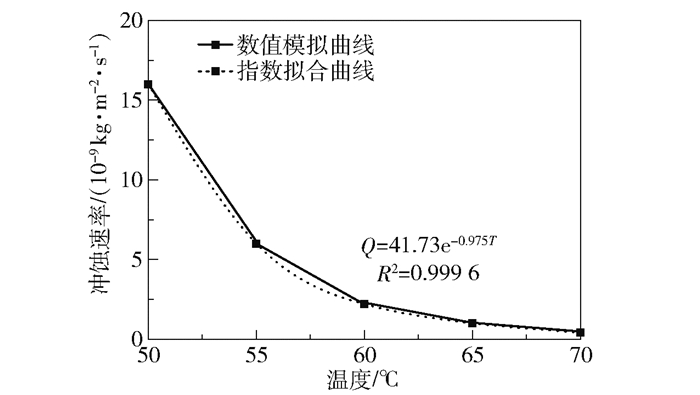
|
图 7 冲蚀速率随稠油温度的变化曲线及拟合曲线 Fig.7 Change curve and fitting curve of erosion rate as a function of heavy oil temperature |
由图 7可知,管道壁面的冲蚀速率随温度的升高而持续下降;通过数据拟合分析可知,二者关系近似为指数函数,函数关系式为Q=41.73e-0.975T,拟合优度R2=0.999 6。
3.2 砂粒粒径对冲蚀速率的影响保持稠油温度50 ℃,砂粒质量流率为0.01 kg/s不变,分析0.1~1.5 mm砂粒粒径(分度值0.1 mm)对管道壁面冲蚀速率的影响。冲蚀速率随砂粒粒径的变化曲线如图 8所示。
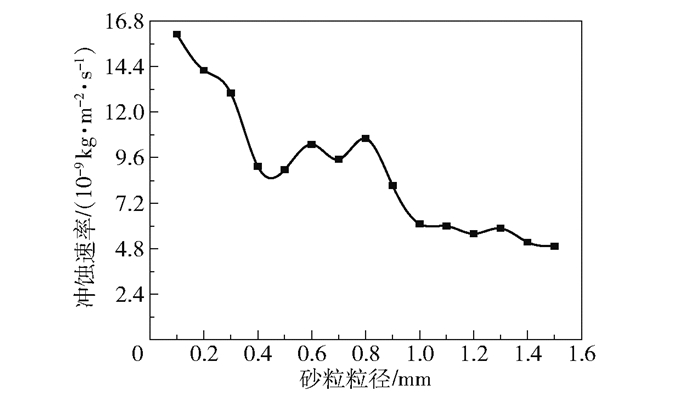
|
图 8 砂粒粒径与冲蚀速率关系曲线 Fig.8 Relationship between sand particle size and erosion rate |
由图 8可知,冲蚀速率随砂粒粒径的增加呈先减小、后稳定、最终减小的变化趋势;当砂粒粒径较小时,冲蚀速率较大,并且其变化幅度也较大,这是由于在砂粒质量流率一定的条件下,砂粒粒径越小则砂粒数目越多,因此由粒径的变化导致所减少的砂粒数较多;当砂粒粒径增大时,冲蚀速率逐渐减小,冲蚀速率变化幅度较平缓;而粒径较大时,稠油中砂粒数目较少,此时砂粒粒径增大相同量时所引起的数量变化相较于之前较小,稠油对砂粒本身的黏性作用平衡了大部分因离心作用产生的惯性力,数量占优的小粒径砂粒在近壁面分布较多,其自身动能受黏性力束缚较小,冲蚀速率较大,而粒径较大的砂粒数量较少,主要分布于流动中心区域,在剪切力的影响下自身动能被有旋流动占据,只有较少一部分砂粒与壁面碰撞,因此冲蚀速率较小[17]。
3.3 质量流率对冲蚀速率的影响保持稠油温度50 ℃,砂粒粒径0.1 mm不变,分析0.01~0.04 kg/s质量流率(分度值0.001 kg/s)对管道壁面冲蚀速率的影响,其冲蚀速率随砂粒质量流率的变化曲线如图 9所示。

|
图 9 砂粒质量流率与冲蚀速率关系曲线 Fig.9 Relationship between mass flow rate of sand grains and erosion rate |
由图 9可知,冲蚀速率随砂粒质量流率的增加而不断增大,这是因为随着砂粒的质量流率增加,主流区介质对管壁附近砂粒的黏性携带作用逐渐加剧,所以冲蚀速率随之增加。由于砂粒粒径保持不变,因此砂粒数目随砂粒质量流率的增加呈线性增长。当砂粒数目增大到一定范围时,管道内壁附近会出现砂粒聚集的现象,因此减缓了主流区砂粒对管壁的冲蚀磨损。
4 结论(1) 在流态不变的情况下,含砂稠油输送管道管壁的冲蚀速率随温度的升高而下降,二者近似呈指数关系,指数拟合优度为0.999 6。
(2) 流体流态及温度恒定时,管道壁面最大冲蚀速率随砂粒粒径的增加而减小,稠油的黏性力对大粒径砂粒的束缚作用较强,因此小粒径砂粒对管壁的冲蚀效果更加严重。
(3) 流体流态及温度恒定时,管道壁面最大冲蚀速率随砂粒质量流率的增加而增大,砂粒数目的增加加剧了近壁面处主流区砂粒的冲蚀作用,稠油与砂粒间接触面积的扩大增强了黏滞力的作用效果,其形成的黏性保护层减缓了冲蚀现象的进一步加剧,因此冲蚀速率趋于平缓。
| [1] |
岳湘安, 陈家琅. 非牛顿流体流动的稳定性参数Y及其应用[J]. 水动力学研究与进展, 1987, 2(3): 114-122. YUE X A, CHEN J L. Non-Newtonian fluid flow stability parameter Y and its application[J]. Advances in Hydrodynamics, 1987, 2(3): 114-122. (in Chinese) |
| [2] |
LIEPSCH D, POLL A. LDA and pressure measurements in a tube with a 90° bend using shear thinning and shear thickening additives in water[M]//SERIZAWA A, FUKANO T, BATAILLE J. Multiphase Flow 1995. Amsterdam: Elsevier Science, 1995: 151-165.
|
| [3] |
顾效源, 潘福奎, 汪文杰, 等. 90°圆截面弯管内稠油流动特性分析[J]. 过程工程学报, 2019, 19(1): 83-90. GU X Y, PAN F K, WANG W J, et al. Numerical simulation on flow characteristics of heavy oil through circular-sectioned 90° bends[J]. The Chinese Journal of Process Engineering, 2019, 19(1): 83-90. (in Chinese) |
| [4] |
刘新锋, 张海龙, 李效波, 等. 海上稠油热采筛管冲蚀影响因素[J]. 石油钻采工艺, 2012, 34(增刊): 73-75. LIU X F, ZHANG H L, LI X B, et al. Influence factors study on screen erosion of offshore heavy crude thermal extraction[J]. Oil Drilling & Production Technology, 2012, 34(Suppl): 73-75. (in Chinese) |
| [5] |
湛含辉, 朱辉, 陈津端, 等. 90°弯管内二次流(迪恩涡)的数值模拟[J]. 锅炉技术, 2010, 41(4): 1-5. ZHAN H H, ZHU H, CHEN J D, et al. Numerical simulation of secondary flow (Dean vortex) in 90° curved tube[J]. Boiler Technology, 2010, 41(4): 1-5. (in Chinese) DOI:10.3969/j.issn.1672-4763.2010.04.001 |
| [6] |
偶国富, 许根富, 朱祖超, 等. 弯管冲蚀失效流固耦合机理及数值模拟[J]. 机械工程学报, 2009, 45(11): 119-124, 132. OU G F, XU G F, ZHU Z C, et al. Fluid-structure interaction mechanism and numerical simulation of elbow erosion failure[J]. Journal of Mechanical Engineering, 2009, 45(11): 119-124, 132. (in Chinese) |
| [7] |
邓智强, 梁晓瑜, 吴欢欢. 原油输运管路冲蚀影响因素仿真研究[J]. 中国测试, 2015, 41(5): 116-120. DENG Z Q, LIANG X Y, WU H H. Simulation studies on erosion wear factors of crude oil transport pipelines[J]. China Measurement & Test, 2015, 41(5): 116-120. (in Chinese) |
| [8] |
王博, 王国付, 王卫强. 含砂原油对45°弯管冲蚀磨损的模拟分析[J]. 辽宁石油化工大学学报, 2019, 39(4): 52-57. WANG B, WANG G F, WANG W Q. Simulation analysis of erosion wear of 45 degree elbow in sandy crude oil[J]. Journal of Liaoning Shihua University, 2019, 39(4): 52-57. (in Chinese) |
| [9] |
FORDER A, THEW M, HARRISON D. A numerical investigation of solid particle erosion experienced within oilfield control valves[J]. Wear, 1998, 216(2): 184-193. DOI:10.1016/S0043-1648(97)00217-2 |
| [10] |
黄波. 地面条件下脱气稠油粘温关系和流变特性研究[J]. 新疆石油学院学报, 2001, 13(1): 66-71. HUANG B. A experimental research into rheological property of heavy oil during gathering and transferring[J]. Journal of Xinjiang Petroleum Institute, 2001, 13(1): 66-71. (in Chinese) |
| [11] |
曲弯弯, 刘刚, 陈雷, 等. 不同剪切条件下胶凝原油轴向与剪切力学特性差异[J]. 油气储运, 2017, 36(5): 526-531. QU W W, LIU G, CHEN L, et al. Differences between axial and shearing mechanical characteristics of gelled crude oil under different shear conditions[J]. Oil & Gas Storage and Transportation, 2017, 36(5): 526-531. (in Chinese) |
| [12] |
ZHU Z F, LIN J Z. Pressure gradient force, Saffman lift, and magnus lift on the fiber-like particle in fluid[J]. Journal of China Textile University (English Edition), 2000, 17(2): 23-27. |
| [13] |
席肖玉.某些与黏性流体力学方程耦合的方程解的相关性质的研究[D].绵阳: 中国工程物理研究院, 2017. XI X Y. Study on the related properties of some equations coupled with viscous fluid mechanics equations[D]. Mianyang: China Academy of Engineering Physics, 2017. (in Chinese) |
| [14] |
苏昆鹏, 吴建华, 夏定康, 等.固体颗粒物运动对磨蚀的影响研究[C]//第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议论文集(上册).合肥, 2019: 284-291. SU K P, WU J H, XIA D K, et al. Influence of solid particle motion on material removal caused by cavitation and abrasion[C]//Proceedings of the 30th National Conference on Hydrodynamics and the 15th National Conference on Hydrodynamics (Volume 1). Hefei, 2019: 284-291. (in Chinese) |
| [15] |
董宇红, 陈林烽, 唐一敏. 存在热浮力的剪切湍流中颗粒近壁运动的大涡模拟[J]. 上海大学学报(自然科学版), 2009, 15(6): 600-606, 627. DONG Y H, CHEN L F, TANG Y M. Large eddy simulation of particle motion in shear turbulent flow due to thermal buoyancy[J]. Journal of Shanghai University (Natural Science), 2009, 15(6): 600-606, 627. (in Chinese) |
| [16] |
张莹.常温输送高含水稠油粘壁机理研究[D].北京: 中国石油大学(北京), 2018. ZHANG Y. Study on the sticky wall mechanism of high water-containing heavy oil transported at room temperature[D]. Beijing: China University of Petroleum(Beijing), 2018. (in Chinese) |
| [17] |
赵联祁.液固两相流弯管冲蚀研究与抗冲蚀优化[D].青岛: 中国石油大学(华东), 2016. ZHAO L Q. Study on liquid-solid two phase elbow erosion and anti-erosion optimization[D]. Qingdao: China University of Petroleum (East China), 2016. (in Chinese) |








