2. 西南交通大学 磁浮技术与磁浮列车教育部重点实验室, 成都 610031
2. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China
轴承作为现代制造业的重要组成部分,在大多数旋转机械的运行中发挥着至关重要的作用,其健康状况直接影响机构性能的稳定性与寿命,因此轴承故障诊断对机械系统运行的可靠性和安全性具有重大意义。在实际应用中,机械系统的工作环境变化很大。由于振动信号容易被噪声污染,因此在工业生产中不可避免地会产生噪声。在嘈杂的环境下诊断故障类型的能力至关重要且具有挑战性。
防止轴承可能损坏的最常见方法是在旋转机构运行时对振动进行实时监控,目前常应用智能的故障诊断方法来识别故障类型[1-3]。Amar等[4]提出了一种故障诊断方法,该方法使用预处理的快速傅里叶变换(fast Fourier transform,FFT)频谱图像作为人工神经网络的输入。从原始振动信号生成的FFT频谱图像首先使用2D平均滤波器进行平均,然后通过适当的阈值选择转换为二进制图像。Shao等[5]针对滚动轴承故障诊断提出一种带有压缩感知的改进卷积深度置信网络,即先用高斯可见单位构造一个新的卷积深度置信模型,以增强压缩数据的特征学习能力;其次采用指数移动平均技术来提高构造的深度模型的泛化性能。
近年来,随着深度学习[6]在各种研究领域中作为计算框架的迅速普及,研究人员尝试使用卷积神经网络(convolutional neural networks,CNN)来诊断机械零件的故障。Wang等[7]提出了一种新的自适应深度卷积神经网络用于滚动轴承的故障诊断:首先,将深度CNN模型进行自动特征学习;其次,采用粒子群算法确定深度CNN模型的主要参数。Janssens等[8]提出一种用于旋转机械状态识别的CNN模型,其输入是从彼此垂直放置的两个传感器收集的两行信号的离散傅里叶变换(discrete Fourier transform,DFT)。Abdeljaber等[9]提出一种自适应1D CNN模型,用来对旋转机械进行检测和定位结构损伤。Guo等[10]提出了一种分层自适应CNN模型,该CNN模型通过将故障位置确定层和故障大小评估层按层次排列来实现故障诊断。以上这些模型在轴承故障诊断方面取得了不错的效果,但是并没有考虑在嘈杂的环境下诊断故障类型的能力,难以保证精度。
综上所述,本文提出了一种基于抗噪多核卷积神经网络(anti-noise multi-core convolutional neural network,AMCNN)的轴承故障识别新方法,在训练中,为增加样本数,抑制过拟合,对原始训练样本进行加噪、重叠采样处理,获得轴承信号样本并实现标签化。然后,根据标签化轴承样本训练改进的AMCNN轴承故障诊断模型,为提高模型抗噪能力,将AMCNN的一层设为dropout层。
1 卷积神经网络CNN的基本结构由正向传播和反向传播组成[11]。正向传播的参数通过反向传播算法进行优化。正向传播由多个卷积层、池化层和几个完全连接的层组成,卷积层的目的是在输入数据通过各层传播时提取它们的不同特征。CNN训练过程如下。
1.1 前向传播步骤1 卷积
卷积阶段的前向传播过程是通过上一层中的节点计算下一个卷积层中节点的过程[12]。第i个特征矩阵表示其输入,第j个特征矩阵表示输出。假设第l个卷积层的第i个偏置参数为bil,特征矩阵的权重为wijl,则其关系表达式为
| $ \mathit{\boldsymbol{y}}_i^l = \sum\limits_i {\mathit{\boldsymbol{y}}_i^{l - 1}} \times \mathit{\boldsymbol{w}}_{ij}^l + \mathit{\boldsymbol{b}}_i^l $ | (1) |
式中,yil是第l个卷积层的第i个输入特征矩阵。
步骤2 批量标准化
在将输入数据映射到非线性函数之前,批量标准化(batch normalization,BN)可减少内部协方差的移位,加快深度神经网络的训练过程,迫使输入数据分布呈标准正态分布。输入到该层的数据落入激活函数的敏感区域,以避免梯度消失。通过始终保持较大梯度的状态,可以调整神经网络的参数以更快地收敛。BN层的转换如下。
| $ {{\mathit{\boldsymbol{\mu }}_{\rm{B}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\mathit{\boldsymbol{y}}_i^l} } $ | (2) |
| $ {\mathit{\boldsymbol{\delta }}_{\rm{B}}^2 = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {\mathit{\boldsymbol{y}}_i^l - {\mathit{\boldsymbol{\mu }}_{\rm{B}}}} \right)}^2}} } $ | (3) |
| $ {\mathit{\boldsymbol{\hat y}}_i^l = \frac{{\mathit{\boldsymbol{y}}_i^l - {\mathit{\boldsymbol{\mu }}_{\rm{B}}}}}{{\sqrt {\mathit{\boldsymbol{\delta }}_{\rm{B}}^2 + \varepsilon } }}} $ | (4) |
| $ {\mathit{\boldsymbol{z}}_i^l = \mathit{\boldsymbol{\gamma }}_i^l\mathit{\boldsymbol{\hat y}}_i^l + \mathit{\boldsymbol{\beta }}_i^l} $ | (5) |
式中,m是每个小批量中y的数目,ε是为保证数值稳定性添加的一个小常数,γil和βil是缩放和移位参数,zil是l个BN层的第i个输出。
步骤3 激活函数
最常见的激活函数为修正线性单元(rectified linear unit,ReLU)[13]。ReLU解决了S型局部梯度爆炸和梯度消失的问题,加速CNN的收敛。ReLU的算法如下。
| $ \mathit{\boldsymbol{c}}_i^l = R\left( {\mathit{\boldsymbol{z}}_i^l} \right) $ | (6) |
式中,R表示ReLU激活函数,cil是zil的激活结果。
步骤4 池化
池化层可以有效地减小矩阵的尺寸,不仅可以加快计算速度,而且可以防止过拟合[14]。通过简单的最大值计算该层的前向传播,转换如下。
| $ \mathit{\boldsymbol{d}}_i^l = \max \left\{ {{\mathit{\boldsymbol{U}}_i}} \right\} $ | (7) |
式中,Ui表示cl的第i个特征矩阵。
步骤5 SoftMax回归
在神经网络的输出进入SoftMax分类之前,执行全连接层。SoftMax回归模型可以是用于优化分类结果的学习算法[15],它将神经网络的输出转换为概率分布,该概率分布绘制了不同事件发生的概率。其转换如下。
| $ y_i^\prime = S\left( {{\mathit{\boldsymbol{d}}_i}} \right) = \frac{{{{\rm{e}}^{{d_i}}}}}{{\sum\limits_{j = 1}^n {{{\rm{e}}^{{d_j}}}} }} $ | (8) |
式中,y′i表示神经网络的第i个预测值,S(·)表示SoftMax函数,di表示汇聚层的第i个输出,n是神经网络预测值的数量。
1.2 反向传播步骤6 交叉熵
交叉熵是评估神经网络输出的指标,它描述了模型的预测分布与真实标签分布之间的距离。输入参数相应标签值y′的交叉熵由神经网络的预测分布y-表示,转换如下。
| $ H\left( {{\mathit{\boldsymbol{y}}^ - },{\mathit{\boldsymbol{y}}^\prime }} \right) = - \sum\limits_i^n {\mathit{\boldsymbol{y}}_i^ - } \lg {\mathit{\boldsymbol{y}}^\prime } $ | (9) |
式中,H(y-,y′)描绘了用y-表达y′的难度。交叉熵是神经网络的损失函数,当交叉熵的值较小时,神经网络的预测值接近真实值。
步骤7 损失函数
损失函数是神经网络优化的目标函数。神经网络的优化是使损伤函数最小化的过程,损失函数值越小,则预测值越接近实际结果,其转换如下。
| $ L(\mathit{\boldsymbol{w}},\mathit{\boldsymbol{b}}) = H\left( {{\mathit{\boldsymbol{y}}^ - },{\mathit{\boldsymbol{y}}^\prime }} \right) + \beta \sum\limits_w {{\mathit{\boldsymbol{w}}^2}} $ | (10) |
式中,L(w, b)是损失函数,它是w和b的函数;β是L2正则化系数;
步骤8 梯度下降
通过梯度下降法对模型的参数进行优化[16],其公式如下。
| $ {\mathit{\boldsymbol{w}}_{ij}^l = \mathit{\boldsymbol{w}}_{ij}^l - \alpha \frac{\partial }{{\partial \mathit{\boldsymbol{w}}_{ij}^l}}L(\mathit{\boldsymbol{w}},\mathit{\boldsymbol{b}})} $ | (11) |
| $ {\mathit{\boldsymbol{b}}_i^l = \mathit{\boldsymbol{b}}_i^l - \alpha \frac{\partial }{{\partial \mathit{\boldsymbol{b}}_i^l}}L(\mathit{\boldsymbol{w}},\mathit{\boldsymbol{b}})} $ | (12) |
式中,α是学习率,
多核卷积是高灵活性的非线性学习模型,本文针对噪声下的轴承信号,采用AMCNN模型来增强模型的提取特征能力,提高识别精度。所提出的AMCNN识别模型建立了12层模型,包括1个输入层、5个卷积层、4个池化层、1个全连接层和1个输出层,第三卷积层采用多核卷积。同时,通过BN方法对数据进行处理。BN层使得输入到该层的数据落入敏感的非线性变换函数区域中,以避免梯度消失。
2.2 数据集增强数据集增强技术通过添加训练样本的方式实现最大化神经连接的通用性目标。AMCNN模型需要大量的训练数据,对于轴承信号的特征,在采样时采用重叠采样的方式以增加训练样本的数量。这种采样方式不仅可以在相邻元素之间保持尽可能多的相关性,同时增加了参与模型的样本数量,从而可以使模型学习到更强的分类特性。
此外,神经网络的训练过程容易造成过拟合,在测试集上的识别率不佳,通用性较差。因此,在测试样本中加入了-10~50 dB信噪比的随机高斯白噪声,以增加有限的样本数量,减弱神经网络的神经元之间的连接关系。加入随机高斯白噪声相当于增加样本,减少神经网络过拟合,高斯白噪声可由下列方法得到。
| $ {{P_n} = {{10}^{\frac{k}{{10}}}}} $ | (13) |
| $ {{P_{{\rm{ave }}}} = \frac{1}{N}\sum\limits_{n = 1}^N {{x^2}} (n)} $ | (14) |
| $ {z = \sqrt {\frac{{{P_{{\rm{ave }}}}}}{{{P_n}}}} {\rm{ }}random{\rm{ }}(N)} $ | (15) |
式中,Pn是噪声序列的功率,Pave是信号序列的平均功率,x(·)是信号序列,N是信号序列中的总点数,k是信噪比,z表示噪声能量的大小。同时,在神经网络的第一层采用了dropout层,模拟真实环境对信号的干扰,以增强神经网络对噪声的抗干扰能力。
最后构建轴承故障识别模型,其结构如图 1所示。首先,将原始信号进行预处理,获得轴承信号样本并实现标签化。然后,根据标签化轴承样本训练改进的AMCNN轴承寿命状态识别模型。在训练过程中,为抑制过拟合对原始训练样本进行加噪、重叠采样处理,为提高模型抗干扰能力,将dropout层作为第一层。
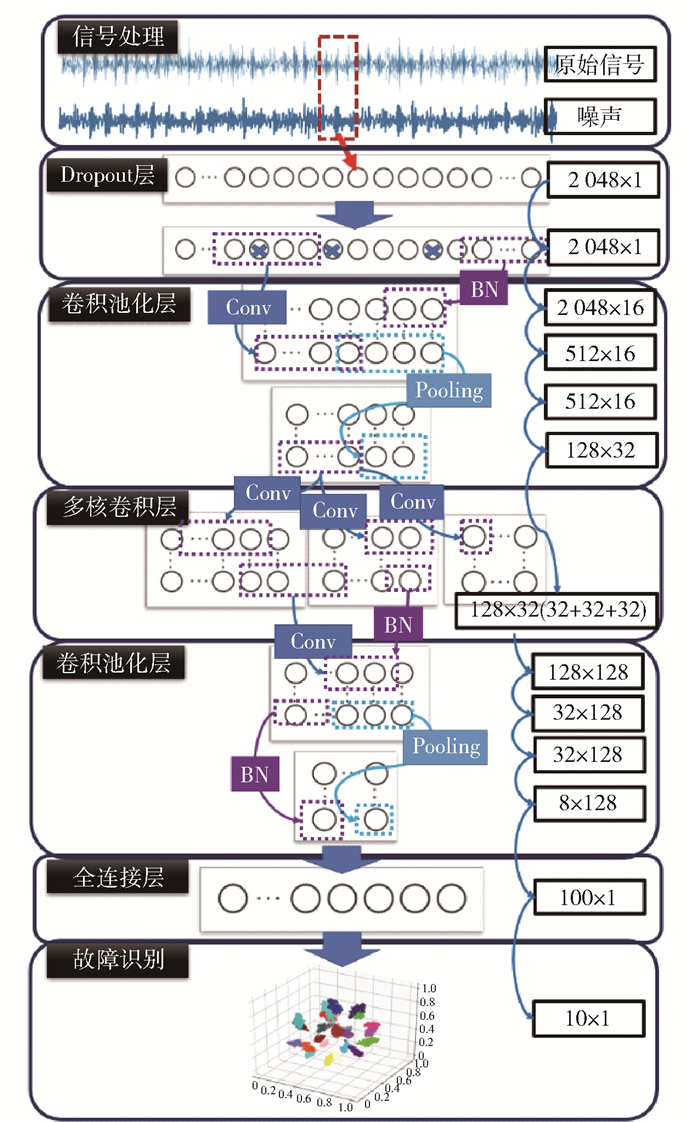
|
图 1 轴承故障识别模型 Fig.1 Bearing fault identification model |
在实际应用中,机械系统的工作环境变化很大,其中主要涉及两种变化:首先,工作负荷可能会随着生产的需要而不断变化,所以需要对训练样本进行分类和标记;其次,工业生产中噪声是不可避免的,振动信号容易受到噪声的污染。
3.1 数据描述实验数据来自美国凯斯西储大学(Case Western Reserve University, CWRU)轴承故障信号,选取了包含无故障样本数据在内的10类数据。分别选取内圈、外圈、滚动体在轻度损伤、中度损伤和重度损伤下的信号各200个样本,采用重叠采样的方式以增加训练样本的数量,每个样本长度为2 048(3种损伤分别采用电火花加工出0.177 8、0.355 6、0.533 4 mm单点故障),另外还包含正常数据共10类数据,采样频率为12 kHz,训练和测试集中的样本个数比为4:1。实验数据详细介绍见文献[18]。
3.2 模型结构参数AMCNN模型各层的参数见表 1。
| 下载CSV 表 1 构建的AMCNN模型参数 Table 1 Parameters of the AMCNN model |
在实验中使用的所提CNN结构由5层卷积和4层池化层组成,紧接着是全连接层和SoftMax层,其中第3层卷积层是由多核卷积核组成,实验使用Google的TensorFlow工具箱实现。第一个卷积内核的大小为1×64,合适的第一个卷积内核可以起到抗干扰作用[19, 10],第3层多核卷积核的尺寸分别为1×1、1×4、1×8、1×16,多核卷积核对复杂特征提取能力更强,更具鲁棒性,能够更好适用于噪声环境。卷积层其余内核大小为1×4,激活函数为ReLU。池化类型为最大池化,在每个卷积层和全连接层之后,批量归一化用于改善CNN的性能。
3.3 CNN模型的可视化本节通过对CNN训练过程的可视化展示模型特征提取过程。选用t分布随机领域嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法,通过基于具有多个特征数据点的相似性识别观察到的模式来找出数据中的规律,将高维数据降低到2维以进行可视化,使相似的数据离得更近,不相似的数据离得更远。图 2给出了从每个卷积层通过t-SNE方法提取的1 000个测试样本的特征分布的可视化结果。由图 2可以看出,在最初的特征分布图中,各类的特征分布是不可分的,但最后的全连接层中各个类别的特征点是完全可分的。
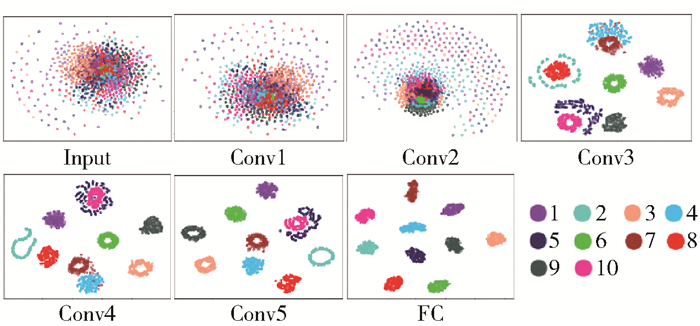
|
图 2 测试样本的特征分布图 Fig.2 Characteristic distributions of test samples |
由此可见,随着层的深入,特征变得越来越可分割,特别是在通过第三层的多核卷积之后,各类特征点的分布有了显著的变化,使得各个类别特征点的分布有了明显的区分,可见多核卷积核在故障分类识别中起到了关键的作用。同时,也验证了所提模型在故障分类上的有效性。
3.4 结果与比较将本文所提模型与其他模型进行对比,验证不同模型性能的优劣。为了检验本文网络模型每个改进部分的效果,设置了3种情形:情形1将传统CNN和AMCNN进行对比,传统CNN结构中无多核卷积核,其他参数与AMCNN参数一致;情形2设置为是否在训练样本中添加噪声;情形3设置为是否添加dropout层作为AMCNN网络模型的第一层,其中dropout的值设为50%[20]。
表 2中比较了不同信噪比环境下4种分类模型的识别正确率。
| 下载CSV 表 2 不同信噪比环境下不同模型识别正确率 Table 2 Accuracy of different models in different environments |
AMCNN为文中所提出的方法,对训练样本进行加噪处理,第一层为dropout层;CNN模型为传统CNN结构,训练样本加噪,第一层为dropout层;AMCNN(无dropout)模型为采用AMCNN结构,训练样本加噪,第一层无dropout层;AMCNN(未加噪)模型为采用AMCNN结构,训练样本未加噪,第一层为dropout层。
由表 2可以看出,当SNR为10 dB时,所有模型均显示出更高的精度(接近100%的正确率)。随着SNR的增加,CNN的准确性大大提升。CNN模型、AMCNN(无dropout)模型、AMCNN(未加噪)模型在SNR从-10 dB上升到10 dB时,正确率从10%~20%显著上升到接近100%。相比之下,AMCNN模型最为稳定,从-10 dB下的36%到10 dB下的99.66%。AMCNN模型在高噪声环境下的正确率都大大高于其他模型,如在-10 dB下,AMCNN模型的正确率比其他模型高出15%~25%,体现出本文所提方法的优越性,即在噪声环境下良好的抗噪能力和极高的故障诊断能力。
随着信噪比的上升,4个模型的识别正确率均呈现上升趋势,在信噪比高于6 dB的环境中,4个模型的识别正确率都能到达到99%以上,AMCNN模型与其余模型相比识别正确率差值小于0.32%。显然,随着信噪比进一步上升,4个模型识别正确率的差别将会越来越小,均接近100%。但在高噪声环境下,AMCNN模型与CNN模型相比,在-10 dB环境下识别正确率高出20.75%,在-8 dB环境下高出11.24%,表明在高噪声环境下AMCNN模型比传统CNN模型在抗噪能力上更优。同理,比较AMCNN模型与AMCNN(无dropout)模型,AMCNN模型的识别正确率在-10 dB环境下高出14.70%,在-8 dB环境下高出17.79%,在AMCNN模型的第一层中加入dropout层会使得识别模型在高噪声下的表现更加良好,比未改进前的AMCNN模型具有更好的抗噪能力。比较AMCNN模型与AMCNN(未加噪)模型,AMCNN模型的识别正确率在-10 dB环境下高出23.99%,在-8 dB环境下高出26.53%,表明加入噪声训练方法的样本可以抑制模型的过拟合,使得识别模型在高噪声环境下的表现更优。综上,这些实验验证了在低噪声环境下,本文所提模型能够实现高识别正确率(达99%以上),同时在高噪声环境下本文的改进部分具有有效性,比其他模型具有更高的识别率。
表 3为支持向量机(support vector machine, SVM)、深度神经网络(DNN)、convolutional neural networks with wide first-layer kernels (WDCNN)[21]、多层感知器(MLP)等模型在信噪比从-5 dB到0 dB环境下对轴承故障的平均识别正确率。
| 下载CSV 表 3 -5 dB到0 dB环境下不同分类模型平均识别正确率 Table 3 Average accuracy of different models in the range -5 dB to 0 dB |
由表 3的比较结果可以看出,本文所提方法在信噪比从-5 dB到0 dB强噪声环境下的平均识别准确度要高于其他方法。主要原因是深度学习方法可以有效地从输入数据中学习基本特征,SVM等传统方法的效率在很大程度上取决于人工牵引;同时,本文针对噪声环境对模型进行了改进,其表现出的效果比部分神经网络算法更好。本文针对噪声环境改进了原始结构和参数,在从原始特征集中选择最敏感的特征或具有优异特性的一些新特征后,诊断结果将得到进一步改善。与人工提取特征的传统方法和其他深度学习方法相比,本文提出方法自动特征学习能力更强大。
4 结论(1) 本文提出了一种新的解决故障诊断问题模型AMCNN,包括两个主要的抗干扰结构,即多核卷积核和外加dropout层,其中多卷核结构通过使用不同大小的卷积核对输入信号进行并行处理以增加模型的宽度,使得模型对复杂特征提取能力更强。AMCNN直接处理原始振动信号,无需任何费时的人工特征提取过程,为抑制过拟合,对原始训练样本进行加噪处理;为提高模型抗干扰能力,将dropout层作为AMCNN的第一层。
(2) 针对在噪声环境下的轴承信号,所提出的带有dropout结构的模型相比其他模型对噪声的容忍度更高;所提出的样本数据加噪的训练方法有效地抑制了神经网络的过拟合问题。
(3) 实验验证结果表明相较于其他模型,本文所提出的AMCNN的网络结构在噪声环境下对故障类型具有更好的识别率,在信噪比从-5 dB到0 dB强噪声环境下的平均识别正确率为94.21%。
| [1] |
JIANG H K, LI X Q, SHAO H D, et al. Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network[J]. Measurement Science and Technology, 2018, 29(6): 065107. DOI:10.1088/1361-6501/aab945 |
| [2] |
KELLEY D R, RESHEF Y A, BILESCHI M, et al. Sequential regulatory activity prediction across chromosomes with convolutional neural networks[J]. Genome Research, 2018, 28(5): 739-750. DOI:10.1101/gr.227819.117 |
| [3] |
SHAO H D, JIANG H K, LI X Q, et al. Intelligent fault diagnosis of rolling bearing using deep wavelet auto-encoder with extreme learning machine[J]. Knowledge-Based Systems, 2018, 140: 1-14. DOI:10.1016/j.knosys.2017.10.024 |
| [4] |
AMAR M, GONDAL I, WILSON C. Vibration spectrum imaging:a novel bearing fault classification approach[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 494-502. DOI:10.1109/TIE.2014.2327555 |
| [5] |
SHAO H D, JIANG H K, ZHANG H Z, et al. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing[J]. Mechanical Systems and Signal Processing, 2018, 100: 743-765. DOI:10.1016/j.ymssp.2017.08.002 |
| [6] |
段艳杰, 吕宜生, 张杰, 等. 深度学习在控制领域的研究现状与展望[J]. 自动化学报, 2016, 42(5): 643-654. DUAN Y J, LV Y S, ZHANG J, et al. Deep learning for control:the state of the art and prospects[J]. Acta Automatica Sinica, 2016, 42(5): 643-654. (in Chinese) |
| [7] |
WANG F, JIANG H K, SHAO H D, et al. An adaptive deep convolutional neural network for rolling bearing fault diagnosis[J]. Measurement Science and Technology, 2017, 28(9): 095005. DOI:10.1088/1361-6501/aa6e22 |
| [8] |
JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound and Vibration, 2016, 377: 331-345. DOI:10.1016/j.jsv.2016.05.027 |
| [9] |
ABDELJABER O, AVCI O, KIRANYAZ S, et al. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks[J]. Journal of Sound and Vibration, 2017, 388: 154-170. DOI:10.1016/j.jsv.2016.10.043 |
| [10] |
GUO X J, CHEN L, SHEN C Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis[J]. Measurement, 2016, 93: 490-502. DOI:10.1016/j.measurement.2016.07.054 |
| [11] |
任浩, 屈剑锋, 柴毅, 等. 深度学习在故障诊断领域中的研究现状与挑战[J]. 控制与决策, 2017, 32(8): 1345-1358. REN H, QU J F, CHAI Y, et al. Deep learning for fault diagnosis:the state of the art and challenge[J]. Control and Decision, 2017, 32(8): 1345-1358. (in Chinese) |
| [12] |
佘道明, 贾民平.一种新型多层深度卷积神经网络的滚动轴承故障诊断方法[C]//中国振动工程学会、南京航空航天大学机械结构力学及控制国家重点实验室.第十二届全国振动理论及应用学术会议论文集.南宁, 2017: 7. SHE D M, JIA M P. A novel multilayer deep learning convolutional neural network method to identify rolling bearing fault[C]//Chinese Society for Vibration Engineering, State Key Laboratory of Mechanical Structure Mechanics and Control, Nanjing University of Aeronautics and Astronautics. Proceedings of the 12th National Conference on Vibration Theory and Application. Nanning, 2017: 7. (in Chinese) |
| [13] |
李伟, 张旭东. 基于卷积神经网络的深度图像超分辨率重建方法[J]. 电子测量与仪器学报, 2017, 31(12): 1918-1928. LI W, ZHANG X D. Depth image super-resolution reconstruction based on convolution neural network[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(12): 1918-1928. (in Chinese) |
| [14] |
周奇才, 刘星辰, 赵炯, 等. 旋转机械一维深度卷积神经网络故障诊断研究[J]. 振动与冲击, 2018, 37(23): 31-37. ZHOU Q C, LIU X C, ZHAO J, et al. Fault diagnosis for rotating machinery based on 1D depth convolutional neural network[J]. Journal of Vibration and Shock, 2018, 37(23): 31-37. (in Chinese) |
| [15] |
郭亮, 高宏力, 张一文, 等. 基于深度学习理论的轴承状态识别研究[J]. 振动与冲击, 2016, 35(12): 166-170, 195. GUO L, GAO H L, ZHANG Y W, et al. Research on bearing condition monitoring based on deep learning[J]. Journal of Vibration and Shock, 2016, 35(12): 166-170, 195. (in Chinese) |
| [16] |
李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124-131. LI H, ZHANG Q, QIN X R, et al. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolution neural network[J]. Journal of Vibration and Shock, 2018, 37(19): 124-131. (in Chinese) |
| [17] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [18] |
LOU X S, LOPARO K A. Bearing fault diagnosis based on wavelet transform and fuzzy inference[J]. Mechanical Systems and Signal Processing, 2004, 18(5): 1077-1095. DOI:10.1016/S0888-3270(03)00077-3 |
| [19] |
GAN M, WANG C, ZHU C A. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2016, 72/73: 92-104. DOI:10.1016/j.ymssp.2015.11.014 |
| [20] |
SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout:a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15: 1929-1958. |
| [21] |
ZHANG W, PENG G L, LI C H, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors, 2017, 17(2): 425. DOI:10.3390/s17020425 |







